Как вводится критерий регулярности.
Предположим, что исходные данные разделены на два непересекающихся подмножества (части выборки 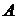 и
и 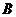 ). В матричных обозначениях:
). В матричных обозначениях: 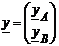 ,
, 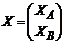 , размерности таковы:
, размерности таковы: 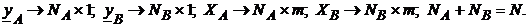
Где 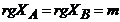 . Критерии точности – критерий, выражающие ошибку проверяемой модели на различных частях выборки. Типичным критерием этого вида является критерий регулярности:
. Критерии точности – критерий, выражающие ошибку проверяемой модели на различных частях выборки. Типичным критерием этого вида является критерий регулярности: 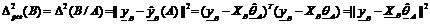 , где запись
, где запись 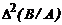 означает «ошибка на
означает «ошибка на 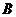 модели, коэффициенты которой получены на
модели, коэффициенты которой получены на 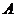 »,
», 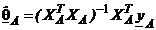 ,
, 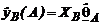 . Этот критерий несимметричен.
. Этот критерий несимметричен.
Ещё один несимметричный критерий регулярности получим, меняя 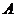 и
и 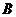 местами:
местами: 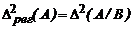 . Теперь несложно сконструировать известный симметричный критерий регулярности:
. Теперь несложно сконструировать известный симметричный критерий регулярности: 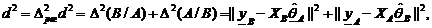
где части 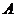 и
и 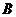 используются равноправно.
используются равноправно.
Покомпонентное МНК – оценивание.
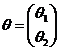 - вектор параметров,
- вектор параметров, 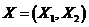 - матрица наблюдений.
- матрица наблюдений.
Выпишем систему нормальных уравнений:
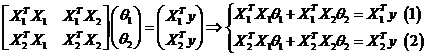
Из уравнения 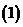 найдем оценку для
найдем оценку для 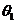 :
: 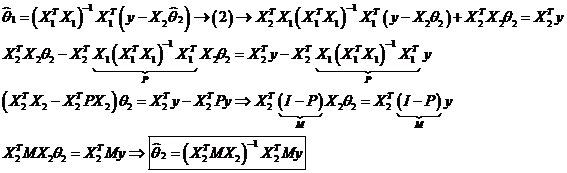 .
.
Как узнать какие именно входные факторы ответственны за возникновение эффекта мультиколлинеарности?
Для этого надо воспользоваться такой мерой мультиколлинеарности как минимальное собственное число матрицы 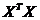 . Пусть
. Пусть 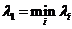 , где
, где 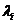 - собственное число матрицы
- собственное число матрицы 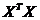 . Предположим, что между
. Предположим, что между 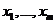 имеется приближенная линейная зависимость, т.е.
имеется приближенная линейная зависимость, т.е. 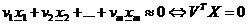 . Вектор
. Вектор 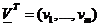 , соответствующий минимальному собственному числу
, соответствующий минимальному собственному числу 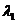 , даёт тот набор коэффициентов, который дает максимальное приближение к нулю линейной комбинации векторов
, даёт тот набор коэффициентов, который дает максимальное приближение к нулю линейной комбинации векторов 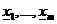 . Тогда эффект мультиколлинеарности создают те регрессоры коэффициенты
. Тогда эффект мультиколлинеарности создают те регрессоры коэффициенты 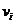 при которых значительно отличаются от нуля.
при которых значительно отличаются от нуля.
|
|
|
Наилучшие линейные оценки. Теорема Гаусса-Маркова.
Для модели наблюдения 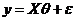 НЛО является оценка
НЛО является оценка 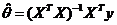 .
.
1. Несмещенность. 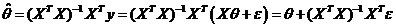
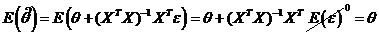
Эффективность.
Пусть 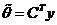 - произвольная несмещенная оценка, т.е.
- произвольная несмещенная оценка, т.е. 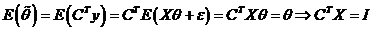 .
.
Обозначим 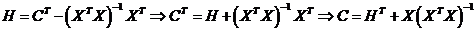 .
.
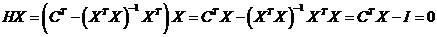 , т.е.
, т.е. 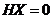 .
.
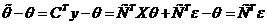
Вычислим матрицу ковариаций для оценки 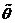 :
:
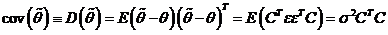
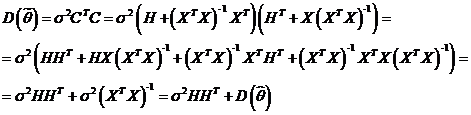
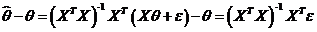
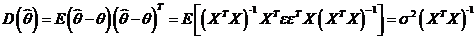
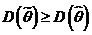 .
.
Состоятельность.
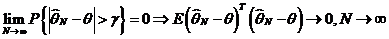
Сходимость в средне – квадратичном ведет в сходимости по вероятности. Воспользуемся неравенством Чебышева:
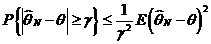 ;
; 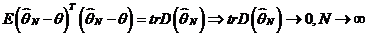
Используем более общее условие - 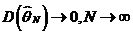 .
.
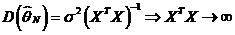
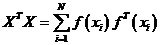 - положительно полуопределенная матрица.
- положительно полуопределенная матрица.
Тогда имея 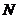 - наблюдений, мы можем добавить
- наблюдений, мы можем добавить 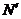 наблюдений:
наблюдений:
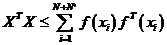 , т.е. она неуклонно возрастает. Тогда Мы можем ожидать, что
, т.е. она неуклонно возрастает. Тогда Мы можем ожидать, что
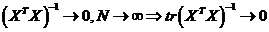 .
.
Ридж оценки неизвестных параметров и их свойства.
С целью управления масштабом оценок введем в рассмотрение функцию стоимости
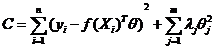 ,
,
где второе слагаемое рассматривается как штраф при условии, что 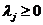 . Решим данную оптимизационную задачу
. Решим данную оптимизационную задачу 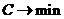 .
.
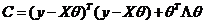 , где
, где 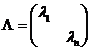 .
.
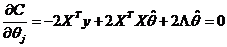 ,
, 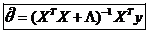 .
.
Часто матрицу 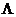 задают в диагональной в виде
задают в диагональной в виде 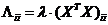 ,
, 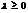 , т.е. пропорциональной диагональным элементам матрицы
, т.е. пропорциональной диагональным элементам матрицы 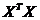 . Иногда применяют ещё более простой вариант
. Иногда применяют ещё более простой вариант 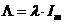 . Покажем, что этот случай эквивалентен первому.
. Покажем, что этот случай эквивалентен первому.
Обозначим
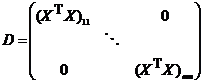 ,
,
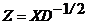 ,
, 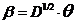 .
.
Тогда исходная модель 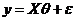 сводится в новых обозначениях к модели
сводится в новых обозначениях к модели
|
|
|
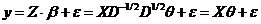 .
.
Ридж-оценка 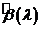 с матрицей
с матрицей 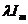 будет равна
будет равна
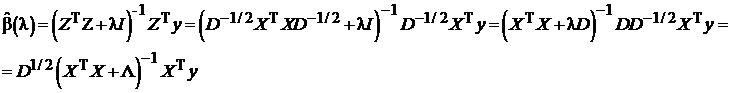 ,
,
где 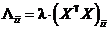 . Поэтому
. Поэтому 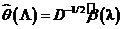 .
.
Итак, можно рассматривать более простой случай
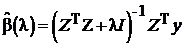 .
.
Свойства этой оценки:
1) 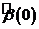 - МНК-оценка
- МНК-оценка 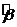 ;
;
2) 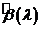 - является линейным преобразованием МНК-оценки и является смещённой;
- является линейным преобразованием МНК-оценки и является смещённой;
Действительно,
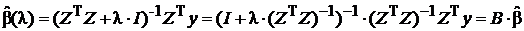 ,
,
где 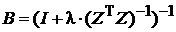 - матрица линейного преобразования.
- матрица линейного преобразования.
3) в классе оценок с фиксированной длиной ридж-оценка минимизирует сумму квадратов отклонений;
4) верно и обратное утверждение: ридж-оценка имеет минимальную длину в классе оценок с заданным значением суммы квадратов отклонений (RSS).
Вариант 4.
Дата добавления: 2018-08-06; просмотров: 273; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
