Галилей перед судом Святой инквизиции
В этом труде Галилей хотел рассмотреть все существующие аргументы в защиту этих двух систем мира. Он положил на чашу весов факты и доказательства, отбросив невежественные рассуждения и авторитеты. В диалоге представителя аристотелевского направления каждый раз побеждает Сальвиати, благодаря своей диалектике и более серьезным аргументам. И все же Галилей с самого начала хотел соблюсти приличия и уточнял, что рассматривает теорию Коперника «как чисто математическую гипотезу». В полном названии он также добавил: «...в котором на протяжении четырех дней рассуждается о двух главнейших системах мира — птолемеевой и коперниковой, беспристрастно рассматривая философские и естественные доводы обеих сторон». Но несмотря на заголовок, любому читателю становилось ясно преимущество гелиоцентризма, в то время как геоцентрическая теория, отстаиваемая Симпличио, постоянно выставлялась нелепой.
ПЕРЕД ИНКВИЗИЦИЕЙ
Попав в Рим, книга Галилея стала настоящей сенсацией и вызвала ожесточенные споры. Заклятые враги ученого, такие как Шайнер и Грасси, были возмущены и книгой, и ее автором.
После многих лет и бурных обсуждений у злопыхателей появилась хорошая возможность напасть на него. Даже папа римский Урбан VIII перешел на сторону противников Галилея после того, как увидел, что его слова, сказанные при разрешении на публикацию книги, были вложены в уста Симпличио. Естественно, папа решил, что прообразом Симпличио стал он сам, что Галилей посмеялся над ним, сделал его предметом сатиры и должен дорого поплатиться за это оскорбление, пусть и невольное.
|
|
|
Все копии книги были конфискованы, а издателю было запрещено вновь печатать произведение. Это стало неожиданностью для Галилея, ведь он подчинился всем требованиям, внес все правки и изменения, предписанные властями при получении разрешения на издание. Когда друзья Галилея вступились за него перед папой, тот заявил, что ученый обманул его.
И все-таки она вертится!
Фраза, приписываемая Галилею после его отречения перед судом Инквизиции
Механизм Инквизиции был запущен после публикации книги, хотя она получила все разрешения для издания. Во Флоренции Галилею сообщили, что Инквизиция начала процесс против него. В конце 1632 года папа потребовал, чтобы ученый вернулся в Рим, но больному 69-летнему Галилею пришлось отложить поездку до начала 1633 года.
В обвинении говорилось, что Галилей нарушил закон 1616 года, запрещающий упоминать о системе Коперника. Его подвергли суровым допросам и в итоге вырвали признание под угрозой пыток. Галилей сдался.
|
|
|
Его исповедь стала достаточным доказательством для того, чтобы признать его виновным. Папа требовал для ученого пожизненного заключения, чтобы другие опасались следовать его примеру. Но ему было недостаточно добиться такого вердикта — папа приказал его обнародовать.
В церкви Санта-Мария-сопра-Минерва 22 июня был оглашен приговор, в котором ученый признавался «серьезно замешанным в ереси», и Галилей прочитал текст отречения, написанный папой. Чтобы сделать поражение Галилея еще более унизительным, приговору был дан большой резонанс. Все труды ученого были включены в Индекс запрещенных книг. После этого папа все-таки позволил изменить пожизненное заключение на пожизненный домашний арест. Судебный процесс стал для Галилея большим потрясением.
УЕДИНЕННАЯ ЖИЗНЬ
Сначала Галилей содержался во дворце архиепископа в Сиене, где за ним тщательно ухаживали. Впоследствии ему удалось добиться переезда в Арчетри, вблизи Флоренции, где располагался монастырь, в котором жили его дочери. Но судьба готовила для него еще один жестокий удар: его любимая дочь, Мария Челеста, умерла в 1634 году в возрасте 33 лет. Старость, изоляция, на которую осудила его Инквизиция, смерть дочери, казалось, положили конец всем задумкам, которые воодушевляли ученого. Но несмотря ни на что у Галилея хватило сил на работу над своим самым амбициозным проектом — созданием новой науки о движении, над которой он думал уже десятки лет.
|
|
|
В 1636 году ученый закончил «Беседы и математические доказательства...». Из-за цензуры, под которую попадали его работы и которая была действительна во всех католических странах, для печати рукописи Галилею пришлось отправить ее в Нидерланды, что вызвало гнев иезуитов, усмотревших в этом насмешку над приговором. Английский философ Томас Гоббс (1588-1679) во время своего визита к ученому рассказал ему, что уже появились переводы его фундаментального труда на английский язык. В 1638 году Галилея посетил Джон Мильтон (1608-1674), который описал эту встречу в своей «Ареопагитике», где страстно отстаивал свободу мысли от цензуры.

Во время домашнего ареста Галилей жил на вилле в Арчетри, недалеко от Флоренции и от монастыря, где находились обе его дочери. Ученый смог провести немного времени с Марией Челестой, которая вскоре умерла. Гравюра Гастона Тиссандье «Мученики науки» (1879).

Надгробный памятник Галилею в базилике Санта-Кроче во Флоренции работы Джованни Баттисты Фоджини. Ученый в правой руке держит телескоп, а левой опирается на глобус, стоящий на книгах.
|
|
|

Винченцо Вивиани и Галилей на картине Тито Лесси 1892 года. Вивиани стал спутником Галилея в годы домашнего ареста, а впоследствии — его первым биографом.
ЛИБРАЦИЯ
Обычно мы видим освещенной только одну сторону Луны, всегда одну и ту же, поскольку период ее вращения вокруг своей оси совпадает с периодом вращения вокруг Земли. Это означает, что теоретически возможно увидеть ровно половину лунной поверхности. И тем не менее терпеливый наблюдатель заметит, что с Земли видно до 59% поверхности Луны, так как в определенные моменты становятся видимыми области, находящиеся в полутени. Это явление объясняется характерными движениями спутника, называемыми либрацией. Этимологически этот термин относится к слову «либра» («весы»), что подразумевает колебательное движение оси. Либрация происходит вследствие нескольких причин. Во-первых, ось Луны наклонена по отношению к плоскости ее орбиты вокруг Земли, поэтому ее движение уже подвержено смещениям. Во-вторых, орбита Луны эллиптическая и в самой дальней ее точке (апогее) наш спутник движется с меньшей скоростью, чем в ближайшей (перигее), так что иногда она вращается вокруг своей оси быстрее, а иногда медленнее, чем вокруг Земли. Наконец, Луна немного колеблется. Галилей описал феномен либрации следующим образом (показав тем самым, что понял, комбинацией каких факторов оно вызвано):
«Я наблюдал удивительный аспект лунной поверхности. Хотя на нее смотрели миллионы людей миллионы раз, думаю, никто не заметил ни малейшего изменения ее поверхности, но всегда видел ту же самую сторону, которая, как всегда считали, предстает перед нашим взором. Теперь я вижу, что это не так, а напротив, она меняет облик, как если бы кто-то, смотря на нас в анфас, немного наклонил голову сначала направо, потом налево, поднял ее, опустил и, наконец, наклонил».
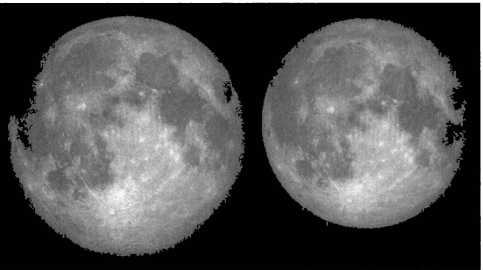
Изображения Луны в точке перигея(слева) и апогея. Сравнив на этих фотографиях расположение некоторых географических областей, снятых со спутника, видно, что Луна не всегда показывает нам в точности одну и ту же сторону.
В 1637 году Галилей сделал еще одно научное открытие — либрацию Луны. Это был его последний вклад в науку: год спустя ученый потерял зрение. В письме другу Галилей так описывает свое положение:
«Твой дорогой друг и слуга Галилей уже несколько месяцев полностью слеп, и это небо, эта Земля, и эта Вселенная, которые я своими небывалыми открытиями и бесспорными доказательствами расширил в сто тысяч раз по сравнению с тем, что о них думали мудрецы прошлого, сейчас сократились для меня до одних телесных ощущений, заполняющих мои дни».
В 1639 году к Галилею переселился его ученик Винченцо Вивиани, который стал первым биографом ученого. Галилей умер 8 января 1642 года, в том же году, когда родился Исаак Ньютон.
Приложение
МАССА И СИЛА ПРИТЯЖЕНИЯ
Галилей предвидел, что в результате эксперимента, подобного тому, что проделали американские космонавты с молотком и пером, оба предмета упадут на поверхность одновременно. Его опыты с наклонной плоскостью во время изучения свободного падения показали, что скорость, развиваемая шарами, зависит только от высоты плоскости, а не от их веса. Таким образом, ученый обосновал свои заключения эмпирическими данными, но не стал объяснять причины этого явления (он систематически воздерживался от безосновательных измышлений), поскольку недостаточно разработал математические методы, способные доказать независимость массы от скорости падения тел.
Исходя из принципов Ньютона возможно математически показать, что скорость, приобретаемая телом во время свободного падения, зависит исключительно от силы притяжения, а не от массы. К тому же, зная радиус и массу планет и спутников, мы можем рассчитать значение ускорения свободного падения на их поверхности.
По Ньютону, между любыми массами возникает притяжение. При помощи своего закона всемирного тяготения он рассчитал эту силу и установил, что она прямо пропорциональна массе двух тел (m1 и m2) и обратно пропорциональна квадрату расстояния между этими телами (d). В соответствии с этим, закон всемирного тяготения выглядит так:
F=G·(m1-m2)/d²
где G — гравитационная постоянная, равная 6,67·10-11 Н·м²/кг².
Вместо взаимодействия двух масс представим себе единое тело, которое ни с чем не взаимодействует. В этом случае, хотя оно и не действует непосредственно ни на какое другое тело, предполагается, что вокруг него создается некое поле, так, что как только другое тело приблизится к этому полю, то сразу же попадет под его влияние. Это гравитационное поле можно изобразить в виде линий, направленных в центр притяжения, то есть к телу (рис. 1).
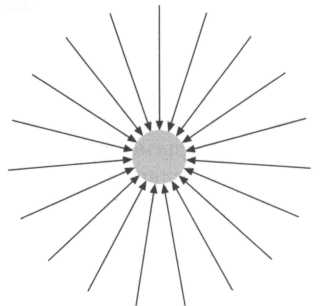
РИС. 1
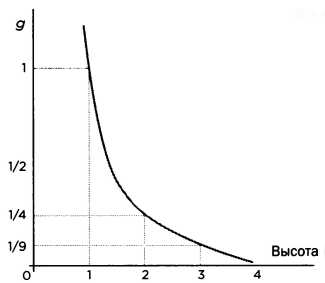
РИС. 2
Значение гравитационного поля можно рассчитать по следующей формуле:
g=G·m1/d² [1]
По этому уравнению мы видим, какое влияние будет оказано на любую массу m2, которая находится на некотором расстоянии от первого тела. Для этого надо будет просто вычислить F=m2g.
Изучив уравнение гравитационного поля, мы увидим, что при увеличении расстояния от центра массы, создающей это поле, уменьшается его интенсивность. Уменьшение силы тяготения в зависимости от высоты можно изобразить в виде графика (рис. 2).
Если в формулу [1] мы подставим массу Земли, а в качестве расстояния возьмем средний радиус Земли:
— масса Земли: М3 = 5,9736·1024 кг;
— радиус Земли: d = 6371 км = 6,371·106 м; то получим следующий результат:
g=G·M2/d2 = 6,67·10-11 Η·м2/кг2·(5,9736·1024 кг)/(6,371-106)2 м2 =9,81 м/с2.
Таким образом, на уровне моря все тела имеют одинаковое ускорение (9,81 м/с2).
С помощью этой же формулы можно вычислить интенсивность гравитационного поля на вершине горы или показать, как уменьшается его значение в зависимости от высоты. Эти расчеты можно произвести и применительно к Луне:
— масса Луны: Мл = 7,349·1022 кг;
— радиус Луны: 1,738 106 м;
g=G·Мл/d2 = 6,67·10-11 Η·м2/кг2·7,349·1022 кг/(1,738- 106)2м2 =1,62 м/с2.
Так мы можем получить значение ускорения на Земле и на Луне. Зная радиус и массу любой планеты или спутника, можно вычислить ускорение свободного падения. Чем крупнее и плотнее планета, тем больше будет значение, определяющее ускорение, с которым будут падать на ней тела. Гравитационное поле также определяет, какую скорость должно развить тело, чтобы освободиться от его влияния и удалиться от планеты или спутника.
СВОБОДНОЕ ПАДЕНИЕ И ЭНЕРГИЯ
По законам кинематики положение и скорость тел при свободном падении вычисляются исходя из их массы. Рассчитывая скорость тела во время свободного падения при помощи понятий кинетической энергии (Ec, связанной со скоростью) и потенциальной энергии (Ep, связанной с весом), можно еще раз убедиться, что эта скорость зависит не от массы тела, а только от высоты, на которой оно находится:
Ec = ½mv2
Ep = m·g·h.
Когда мы держим шар на определенной высоте от поверхности, он обладает потенциальной энергией, которая при его падении переходит в кинетическую. Таким образом, для того чтобы узнать, какова будет скорость тела в момент, когда оно коснется земли (то есть когда вся его потенциальная энергия перейдет в кинетическую), нужно использовать формулу:
m·g·h = ½mv2
В результате скорость будет равна:
v = SQRT(2·g·h)
Итак, мы видим, что конечная скорость, с которой двигается тело, не зависит от его массы.
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
Если нам надо рассчитать скорость убегания, то есть скорость, которую должна развить ракета или любое другое тело для того, чтобы преодолеть силу притяжения планеты, можно воспользоваться следующим уравнением. Вначале запишем, чему равна потенциальная энергия гравитации:
En = G(Mз·m)/d
Mз обозначает массу Земли, но в это уравнение можно подставить массу любой другой планеты или спутника. Кинетическая энергия равна:
Ek = ½mv2
Скорость ракеты должна быть достаточной для того, чтобы ее кинетическая энергия стала равной или большей потенциальной энергии планеты:
½mv2 = G(Mз·m)/d
Следовательно, скорость убегания равна:
v = SQRT((2·G·Mз)/d)
Мы снова видим, что эта скорость не зависит от массы тела и всегда одинакова (хотя, если тело будет более тяжелым, ему потребуется больше энергии, чтобы развить такую скорость).
АТМОСФЕРА И ТРЕНИЕ
Атмосфера Земли — причина сопротивления, которое испытывают тела при падении, именно из-за нее они двигаются с разной скоростью. Из двух шаров, сделанных из одинакового материала, более тяжелый упадет быстрее, и только в вакууме они упадут одновременно, как предсказывал Галилей.
Сопротивление воздуха действует как сила, направленная против движения тела. В случае свободного падения его действие направлено противоположно силе притяжения. Это же сопротивление объясняет, почему летают и остаются в воздухе самолеты (хотя, как мы увидим ниже, крылья самолетов используют другие свойства и аэродинамические принципы). Его можно сравнить с сопротивлением поверхности, когда мы пытаемся сдвинуть очень тяжелый предмет.
Воздух, являясь газом, состоит из молекул воды, кислорода, азота и диоксида углерода. Чтобы тело упало, эти молекулы должны сместиться. Чем больше будет падающее тело и чем меньше при этом будет его вес, тем медленнее молекулы будут смещаться, чтобы пропустить его, и, следовательно, тем медленнее будет его падение.
Форма и фронтальная поверхность падающего тела также влияют на скорость, которую оно разовьет. Если мы возьмем лист бумаги, то и его вес, и его поверхность будут способствовать тому, что он будет снижаться медленнее, тогда как стальной шар упадет очень быстро. На планетах или таких спутниках, как Луна, где нет молекул, препятствующих падению тел, их форма и вес не являются определяющими факторами.
ТРЕНИЕ И КВАДРАТ СКОРОСТИ
При рассмотрении предметов, падающих с небольшого расстояния, влиянием сопротивления воздуха обычно можно пренебречь, то есть учитывать его при расчетах не обязательно. Напротив, при значительной высоте необходимо учесть влияние аэродинамического сопротивления.
Трение — это сила, противонаправленная силе притяжения. Когда скорость падающего тела невысока (например, при малой высоте), то сила трения пропорциональна скорости. При большей скорости увеличится и сопротивление воздуха, и это соотношение будет прямо пропорциональным.
В случае тел, развивающих большие скорости, сопротивление увеличивается на величину, пропорциональную квадрату этой скорости. Это увеличение вызвано тем, что при большой скорости образуются воздушные завихрения, которые усиливают действие сопротивления.
Это явление необходимо принимать во внимание при конструировании автомобилей, так как сопротивление воздуха в этом случае является важнейшим фактором (поэтому на стадии проектирования ставится множество опытов, чтобы улучшить их аэродинамику). Когда скорость удваивается, сопротивление воздуха возрастает в четыре раза, когда она утраивается — в девять раз. Чтобы создать очень быстрый автомобиль, необходимо снабдить его мощным мотором.
Действие силы гравитации и трения математически можно записать так:
mg- FR =ma,
где mg — вес предмета, на который действует соответствующая сила притяжения. Сила трения FR, как уже было сказано, пропорциональна квадрату скорости и зависит от различных факторов, которые можно считать константой:
F = kv2
Как уже говорилось, k зависит от таких факторов, как форма предмета, сопротивление воздуха и фронтальная поверхность, которая противостоит этому сопротивлению. Чтобы рассчитать ее значение, используется уравнение:
k = ƒkWS
где ƒ— значение от 0 до 1, зависящее от формы предмета (1 соответствует телу с абсолютно плоской поверхностью; чем лучше будут аэродинамические свойства тела, тем меньше будет это значение); kw — значение сопротивления воздуха, равное 0,6N с2/м4 и, наконец, S обозначает площадь поверхности тела, находящуюся в трении с воздухом.
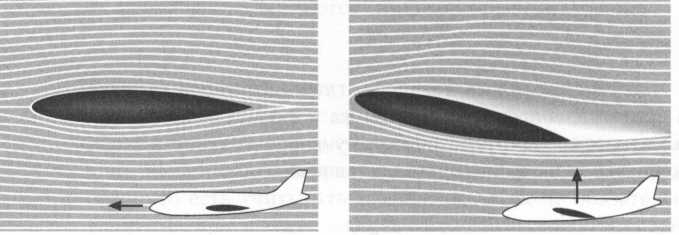
Когда крыло самолета расположено горизонтально, давление воздуха как в нижней части, так и в верхней одинаково. Но когда крыло слегка наклоняется, давление воздуха в нижней части становится выше, чем в верхней, и это позволяет самолету набирать высоту.
ПОЧЕМУ САМОЛЕТЫ ЛЕТАЮТ
Секрет того, почему летают самолеты, заключается в сопротивлении воздуха. Так же как мы, двигая правильным образом руками, держимся на поверхности воды, самолеты используют некоторые характеристики окружающей среды, чтобы «плыть» в воздухе, хотя здесь действуют и другие явления, в частности эффект Вентури (следствие закона Бернулли).
Крылья самолетов спроектированы таким образом, чтобы воздух двигался быстрее в их верхней части, чем в нижней, тем самым используя эффект Вентури, по которому жидкости, проходя через суженную часть трубы, увеличивают свою скорость. Теорема Бернулли гласит, что при увеличении скорости жидкости уменьшается давление. Поэтому в нижней части крыла давление больше, чем в верхней. В результате этой разницы давлений самолет может набирать высоту.
Дата добавления: 2018-08-06; просмотров: 204; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
