ВИДИМЫЕ ПРИЗНАКИ ВРАЩЕНИЯ ЗЕМЛИ
Поскольку Земля вращается, она является неинерциальной системой отсчета, и здесь возникают кажущиеся силы, проявляющиеся в некоторых природных явлениях, например в эффекте Кориолиса и опыте с маятником Фуко, физически доказывающих движение Земли.

Гаспар-Гюстав де Кориолис.
Прямая линия или парабола?
Эффект Кориолиса, названный по фамилии описавшего его в 1835 году ученого, Гаспара-Гюстава де Кориолиса (1792-1843),— это феномен, при котором кажется, что на тело, движущееся на вращающейся поверхности, действует некая сила. Если это тело будет пытаться прямолинейно двигаться вперед во вращающейся системе отсчета, наблюдатель, находящийся в той же подвижной системе, увидит, что тело описывает параболу, и справедливо подумает, что на него действует внешняя сила. Другой наблюдатель, вне этой системы, не увидит никакой параболы, для него предмет будет двигаться по прямой. Мы должны учитывать этот эффект, например, в случае с маршрутами самолетов, соединяющих города на значительном расстоянии друг от друга, иначе самолет, двигаясь по прямой до заданной точки, только отклонялся бы от нее и никогда бы ее не достиг. Этот эффект заметен только на больших расстояниях (на коротких дистанциях им можно совершенно пренебречь, поэтому эффект Кориолиса не влияет на направление закручивания воды в сливе). При таких атмосферных явлениях, как бури или ураганы, сила Кориолиса направляет воздушные массы против часовой стрелки в Северном полушарии и по часовой — в Южном.
|
|
|
Вращение смещает маятник
Французский физик Леон Фуко (1819-1868) продемонстрировал в 1851 году под куполом Пантеона в Париже, что у земного вращения есть видимые признаки. Поскольку колебания маятника остаются неизменными по отношению к инерциальному наблюдателю, когда такой маятник и наблюдатель находятся в неинерциальной системе, возникают фиктивные силы, которые вызывают прецессию движения маятника. Соответственно, Земля не является инерциальной системой отсчета и поэтому не может быть неподвижной.
Принцип инерции связан только с равномерным движением, поэтому еще требовалось найти объяснение движению с ускорением, которое, как впоследствии указал Ньютон, подразумевает приложение некоей силы. Галилей посвятил часть своих опытов и размышлений попытке объяснить ускоренное движение.
ЗАРОЖДЕНИЕ НОВОЙ ТЕОРИИ УСКОРЕННОГО ДВИЖЕНИЯ
Изучая ускоренное движение, Галилей пользовался в первую очередь разработками Архимеда и поставил под вопрос идеи Аристотеля. Впоследствии, уточнив свои эксперименты, он смог установить зависимость пройденного расстояния от времени свободного падения.
|
|
|
ВЕС И СОПРОТИВЛЕНИЕ
В юности Галилей полагал, что при свободном падении тела сохраняют постоянную скорость, а не ускоряются. Однако он не был согласен с Аристотелем и утверждал, что эта скорость пропорциональна разнице между силой и сопротивлением (а не их соотношению). Оба они были неправы, но размышления Галилея показывают, как развивалась его мысль.
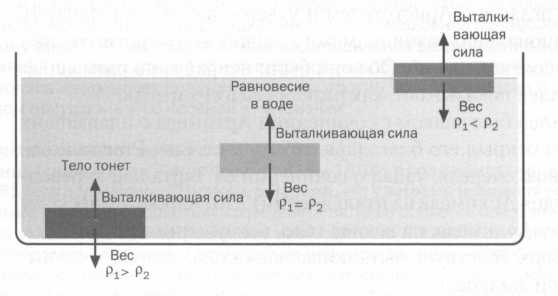
Галилей был знаком с сочинением Архимеда о плавающих телах (он открыл его благодаря своему учителю, Риччи, который, в свою очередь, узнал о сочинении от Тартальи, переводчика трудов Архимеда на итальянский). По гидростатическому принципу Архимеда, на всякое тело, погруженное в жидкость, снизу вверх действует выталкивающая сила, равная весу вытолкнутой жидкости.
Утверждения Архимеда о весе и выталкивающей силе были распространены на все тела, не только на погруженные в воду. Соответственно, вес каждого тела мог меняться в зависимости от сопротивления окружающей среды (Архимед констатировал, что выталкивающая сила меняет вес погруженных тел), и необходимо было иметь в виду разницу между весом и сопротивлением (см. приложение «Атмосфера и трение»).
|
|
|
Изначально Галилей придерживался представлений Аристотеля, полагавшего, что тела падают с постоянной скоростью. Таким образом, скорость пропорциональна разнице между удельным весом тела (Р) и сопротивлением среды (Я, удельный вес воздуха), что сегодня записывается как:
v = k(P-R),
где k — коэффициент пропорциональности. В вакууме сопротивления нет, следовательно, скорость тела пропорциональна его удельному весу. Это уравнение совместимо с понятием вакуума (не существующего в аристотелевской Вселенной). Именно в вакууме тело двигается со своей собственной скоростью, не подверженной сопротивлению среды.
Несмотря на новаторский подход, Галилей продолжал думать, что при свободном падении тела двигаются без ускорения. По его мнению, если ускорение и существовало, то оно возникало только в момент начала движения. Затем скорость становилась постоянной и пропорциональной разнице между удельным весом и сопротивлением среды. Со временем Галилей изменил свое мнение.
УДЕЛЬНЫЙ ВЕС И ПЛОТНОСТЬ
Основываясь на трудах Архимеда, Галилей связал удельный вес тел с их скоростью в свободном падении. Архимед определял удельный вес как вес тела, поделенный на его объем. Погружая предметы в жидкость, он пришел к выводу, что когда удельный вес твердого тела равен удельному весу жидкости, то тело погружается в воду, не касаясь при этом дна, а затем его поверхность поднимается над водой. Если же удельный вес тела больше веса жидкости, то количество вытолкнутой им воды равно его весу. Таким образом, Архимед определил, что существует выталкивающая сила (Е), которая действует на погруженное тело и направляет его вверх, на поверхность, и что эта сила равна разнице между весом вытесненной жидкости и весом погруженного тела.
|
|
|
Плотность (р) тела определяется как отношение массы (т) тела к его объему (V). Математически можно записать так:
p=m/V
Удельный вес (γ), в свою очередь, определяется как отношение веса (Р) к объему (V):
T=P/V
Поскольку вес равен массе, помноженной на ускорение свободного падения, мы получаем следующее равенство:
T=P/V=mg/V=pg
Как мы видим, в то время как плотность — постоянная величина в любой точке Вселенной, удельный вес пропорционален плотности и зависит от ускорения свободного падения (на уровне моря он будет больше, чем на вершине горы, а на более тяжелых планетах его значение будет больше, чем на легких).
КИНЕМАТИКА
В сочинении «Беседы и математические доказательства...», написанном под арестом, когда Галилей был уже стар, перечисляются основные открытия и размышления, сделанные ученым на протяжении всей жизни. Работа стала фундаментом, на котором Ньютон развивал свои идеи, сегодня считающиеся классическими. В книге описано равномерное движение, равномерно ускоренное движение и движение бросаемых тел, или параболическая траектория снарядов.
РАВНОМЕРНОЕ ДВИЖЕНИЕ
В первой и самой короткой части своей книги Галилей выявляет связь между пройденным расстоянием (s) и затраченным временем (t), которая определяет равномерное прямолинейное движение. Записанная при помощи современных математических символов, эта зависимость выглядит следующим образом:
S=v • t
РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ

Момент, когда космонавт Дэвид Скотт кидает молоток и перо на поверхность Луны, чтобы проверить, упадут ли они одновременно.

Страница из «Бесед и математических доказательств...»— труда, в котором Галилей собрал все свои размышления о движении.

Фуко при помощи маятника демонстрирует вращение Земли (рисунок хранится в Политехническом институте Лондона).
Как мы видели в предыдущей главе, Галилей изначально полагал, что движение во время свободного падения было равномерным, а не ускоренным. Впоследствии он пришел к выводу, что оно является ускоренным, но при этом пропорциональным пройденному расстоянию. У нас нет доказательств того, что Галилей нашел правильное решение, а именно, что ускорение пропорционально квадрату времени, до 1604 года. В одном из своих писем к Сарпи, датируемом этим годом, он утверждает следующее:
«Размышляя о движении, [...] я покажу затем остальное, то есть что расстояние, пройденное во время естественного движения, дважды пропорционально времени [...]».
Дата добавления: 2018-08-06; просмотров: 257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
