Исследование устойчивости синтезированной САУ при последовательном введении в ее контур управления нелинейного звена
Все реальные системы являются в большей или меньшей степени нелинейными. Рассмотрение САУ как нелинейной системы становится наиболее важным для практики по мере повышения требований к качеству процессов и к точности расчета САУ.
Наиболее распространенным на практике методом исследования нелинейных систем высшего порядка является метод гармонической линеаризации.
4.1. Гармоническая линеаризация нелинейного звена
Гармоническая линеаризация позволяет заменить нелинейное звено некоторым звеном с передаточной функцией, эквивалентной нелинейному элементу, с целью рассмотрения САУ как линейной системы.
Пусть нелинейное звено описывает функция вида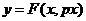 
и задано 
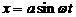и 
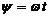. Рассмотрим разложением такой функции в ряд Фурье:
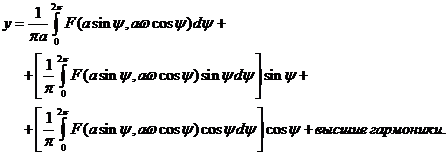
Положим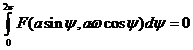 
, что означает отсутствие постоянной составляющей в данном разложении. Тогда, если принять во внимание
, 
,
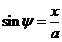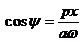то разложение в ряд Фурье функции можно заменить выражением
,
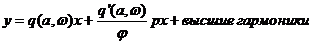которое с точностью до высших гармоник аналогично линейному.
Коэффициенты гармонической линеаризации нелинейного элемента определяются формулами:
,
.
Гармонически линеаризованная передаточная функция нелинейного звена имеет вид:
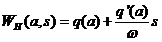. (19)
Амплитудно-фазовая характеристика нелинейного звена в результате подстановки 
в выражение для гармонически линеаризованной передаточной функции:
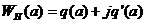. (20)
|
|
|
Рассмотрим нелинейное звено с насыщением без зоны нечувствительности (рисунок 14).
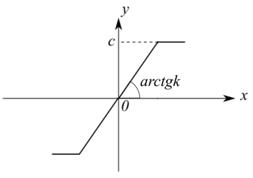
Рисунок 4.1 – Характеристика звена с насыщением без зоны нечувствительности
Ввиду отсутствия гистерезисной петли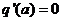 
. Тогда уравнение нелинейного звена с характеристикой такого вида будет 
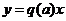, где 
определяется выражением:
.
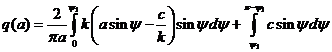Преобразуя выражение, получим:
.
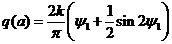С учетом 
, полученное выражение для коэффициента гармонической линеаризации примет вид:
.
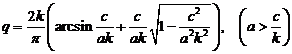При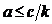 
имеем линейную характеристику 
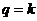. При амплитудах колебания входной величины, захватывающих зону насыщения, данное звено заменяется линейным звеном с тем меньшим коэффициентом усиления 
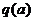, чем больше амплитуда колебания.
Гармонически линеаризованная передаточная функция рассматриваемого нелинейного звена и амплитудно-фазовая характеристика нелинейного звена с зоной нечувствительности без насыщения согласно (19) и (20):
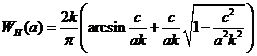. (21)
На рисунках 15, 16 и 17 представлены графики и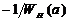 
для различных значений параметров нелинейности c и k.
Рисунок 4.2 – Графики и 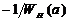при c=1 и k=1
Рисунок 4.3 – Графики и при c=1 и k=5
Рисунок 4.4 – Графики и 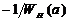при c=5 и k=1
4.2. Определение условий возникновения автоколебаний в САУ
|
|
|
Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах. Благодаря этим особенностям возможен новый вид установившегося процесса – автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению регулируемой величины, часто становится невозможным. Система будет обладать устойчивыми автоколебаниями в том случае, когда колебания в переходных процессах стремятся к одной и той же амплитуде и к одной и той же частоте.
Структурная схема САУ с последовательно введенным в контур управления нелинейным звеномимеет вид, представленный на рисунке 18.
Рисунок 4.5 – Структурная схема САУ с последовательно введенным в контур управления нелинейным звеном
На рисунке 18 в качестве передаточной функции линейной части выступает передаточная функция синтезированной САУ (рисунок 10), которая определяются с помощью MATLAB следующим образом:
ke=199.52;
|
|
|
W1=tf([1],[0.075 1]);
W2=tf([1],[0.0097 1 0]);
W12=W1*W2;
Wob1=tf([0.3 11.97 0],[1]);
Wob2=tf([0.18 0],[0.18 1]);
Wob=Wob1*Wob2;
W0=W12/(1+W12*Wob);
W=ke*W0;
В итоге передаточной функции линейной части:
.
Задача о проверке возможности наличия в данной системе автоколебания является задачей определения устойчивого периодического решения.
Периодическое решение линеаризованной системы получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней. А это по критерию Найквиста соответствует прохождению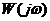 
через точку -1. Следовательно, периодическое решение определяется равенством:
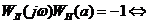
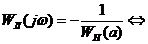
, (22)
где и 
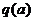– коэффициенты гармонической линеаризации нелинейного элемента.
Уравнения (22) определяет искомую амплитуду а и ω периодического решения. Его можно представить в виде системы уравнений:
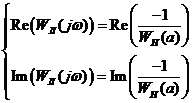. (23)
Функция 
является в данном случае вещественной (рисунки 19, 20, 21) и укладывается вся на отрицательной части вещественной оси. С учетом этого, система уравнений (23) примет вид:
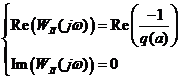. (24)
Для построения амплитудно-фазовой частотной характеристики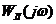 
в «Simulink» используется структурная схема, представленная на рисунке 19.
|
|
|
Рисунок 4.6 – Структурная схема для построения амплитудно-фазовой частотной характеристики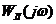
Результат построения амплитудно-фазовой частотной характеристики 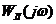приведен на рисунке 20.
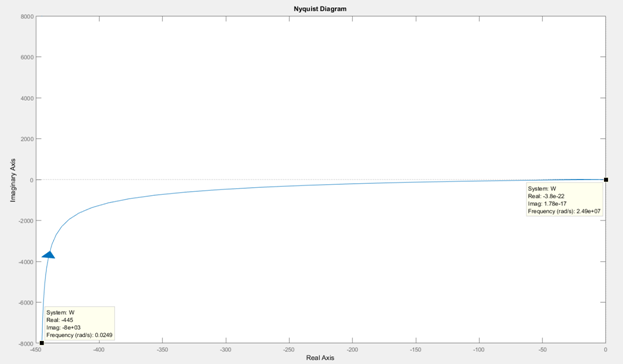
Рисунок 4.7 – Амплитудно-фазовая частотная характеристика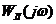
Согласно моделированию, амплитудно-фазовая частотная характеристика 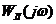пересекает реальную ось в точках с координатами (-0,0327; 0) и (0; 0).
Определим, в каком случае существует периодическое решение линеаризованной системы. Для этого, согласно (24), решим равенство:
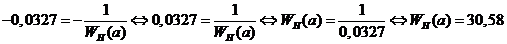(25)
Для проверки правильности произведенных вычислений для САУ с нелинейным элементом, который, согласно (25), заменяется усилительным звеном, построим амплитудно-фазовую частотную характеристику 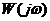(рисунок 21) и смоделируем переходный процесс (рисунок 22).
Рисунок 4.8 – Структурная схема для построения амплитудно-фазовой частотной характеристики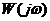
Рисунок 4.9 – Структурная схема для моделирования переходного процесса в САУс нелинейным звеном в контуре управления
Результат построения амплитудно-фазовой частотной характеристики САУ приведен на рисунке 23.
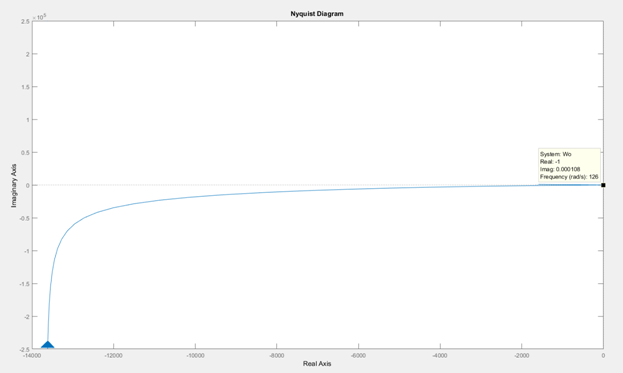
Рисунок 4.10 – Амплитудно-фазовая частотная характеристика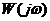
Результат моделирования переходного процесса представлен на рисунке 24.
Рисунок 4.11– Результат моделирования переходного процесса в САУ с нелинейным звеном в контуре управления
Согласно результатам моделирования, в системе наблюдаются автоколебания с амплитудой 
1.9 и частотой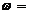 
19.8 Гц.
4.3. Расчет значений параметров нелинейного звена
Рассчитаем значения параметров нелинейного звена, обеспечивающие полученные автоколебания. Согласно (21) и (22):
.
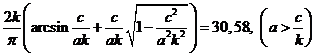Введем замену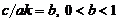 
, тогда второе неравенство системы примет вид:
.
Согласно полученной зависимости, чем больше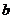 
, тем меньше 
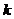. Примем 
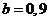, тогда
.
Из введенной замены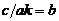 
, принятого ограничения 
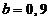, рассчитанного значения 
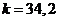и полученной в результате моделирования амплитуды автоколебаний 1,9:
.
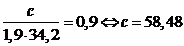Таким образом, при рассчитанных значениях параметров нелинейности в САУ будут возникать автоколебания с амплитудой 1,9 и частотой 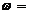19.8 Гц.
Список используемой литературы
1. Maxon academy “Formulae Handbook”, Jan Braun, 2012.
2. Зенкевич С.Л., Ющенко А.С. Основы управления манипуляционными роботами: учебник для вузов. 2-е изд., исправ. и доп. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 480 с.
3. И.К.Хапкина Методика синтеза системы управления электропривода робота, инвариантного к парамерическим и внешним возмущениям,2014
4. Попов Е. П. Теория линейных систем автоматического регулирования и управления. Издательство «Наука», Москва, 1989.
5. Бесекерский В. А., Попов Е. П. Теория систем автоматического управления. Издательство Санкт-Петербург, 2003.
6. Дорф Р., Бишоп Р. Современные системы управления. Пер. с англ. Б. И. Копылова. – М: Лаборатория Базовых Знаний, 2002.
Дата добавления: 2018-08-06; просмотров: 291; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!