Систематические коды Хэмминга.
Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях.
Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Систематические коды могут строиться, как линейные на основе производящей матрицы. Обычно производящая матрица строится при помощи двух матриц: единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее d0 -1 единиц, а сумма по модулю для любых строк не менее d0-2 единиц (где d0 - минимальное кодовое расстояние).
Производящая матрица позволяет находить все остальные кодовые комбинации.
Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Он настолько хорошо изучен, что уже выработался четкий алгоритм его построения.
Код Хэмминга представляет собой один из важнейших классов линейных кодов, нашедших широкое применение на практике и имеющих простой и удобный для технической реализации алгоритм обнаружения и исправления ошибок.
Хэммингом предложено располагать столбцы проверочной матрицы так, чтобы i-й столбец матрицы и номер разряда кодовой комбинации отвечали двоичному представлению числа i. Тогда синдром исправления однократных ошибок будет двоичным представлением номера разряда, в котором произошла ошибка. Для этого проверочные разряды должны находиться не в правой части кодового слова, а в позициях, номера которых являются степенью двойки, т. е. 20, 21, 22, …, 2r-1.
|
|
|
Проверочная матрица (k, n)-кода Хэмминга составляется из n=2r-1 строк и r столбцов и представляет собой двоичные комбинации числа i, где i – номер столбца проверочной матрицы (разряда кодовой комбинации).
Числовой и цифровой метод контроля по модулю.
При числовом методе контроля код заданного числа определяется как наименьший положительный остаток от деления числа на выбранный модуль р:
r∆=A-{A/p}A, где в фигурных скобках {} - целая часть от деления числа; А - контролируемое число.
Величина модуля р существенно влияет на качество контроля; если р = q (q - основание системы счисления, в которой выражено число) и имеет место числовой контроль, то контролируется только младший разряд числа и контроль как таковой не имеет смысла; для p=qm справедливы аналогичные соображения, так как если m<n, то опять не все разряды числа участвуют в контроле и ошибки в разрядах старше m вообще не воспринимаются.
|
|
|
При числовом методе контроля по модулю р для определения остатка используют операцию деления, требующую больших затрат машинного времени. Для числового метода контроля справедливы основные свойства сравнений (сложение, умножение сравнений и т.д.).
При цифровом методе контроля контрольный код числа образуется делением суммы цифр числа на выбранный модуль:  или
или 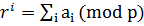 .
.
Возможны два пути получения контрольного кода: 1)непосредственное деление суммы цифр на модуль р; 2) суммирование цифр по модулю р.
Второй путь проще реализуется, так как если аi < р , то контрольный код получается только операцией суммирования.
Однако при цифровом методе свойства сравнений не всегда справедливы, и происходит это из-за наличия переносов (заемов) при выполнении арифметических действий над числами. Поэтому нахождение контрольного кода результата операции происходит обязательно с коррекцией.
Дата добавления: 2018-08-06; просмотров: 426; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
