Определение числового ряда, сумма ряда. Сходящиеся и расходящиеся ряды.
а)Определение: Даны числа: 
;
Числовым рядом называется выражение 
, где 
.
Обозначение: 
б) 
n-я частичная сумма ряда, сумма первых n членов ряда.
Рассмотрим последовательность частичных сумм ряда
…
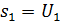
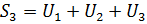
в)Если существует предел последовательности частичных сумм ряда, то этот предел принимается за сумму ряда, а ряд называется сходящимся.
Пусть существует 
, S-сумма ряда, т.е. если 
сходящийся 
или 
Замечание, если 
или не существует, то 
называется расходящимся.
Геометрическая прогрессия, сходимость, доказать.
1) 
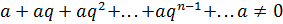
q – знаменатель
2) Найти Sn
a) Если 
б) Если 
в) Если 
г) Если 
Вывод:
1) Если 
2) Если 
Доказать свойство сходящихся рядов.Признаки Коши и Даламбера.Примеры
а)Свойства сходящихся рядов.
Свойство 1.
Пусть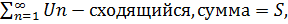 
Тогда 
Доказательство:
1) Дано 
2) Рассмотрим ряд 
Вычислим 
Свойство 2.
Пусть 
Пусть 
=>
Замечание 
Примеры:
Найти S
б)Признаки Коши и Даламбера. Примеры
1.Признак Даламбера.
Вычисляем предел отношения последующего члена ряда к предыдущему
2.Признак Коши.
Если А>1 – ряд расх.
Если А<1 – ряд сход.
Если А=1 ? (проверить необходимый признак)
Пример.
Необходимый признак сходимости ряда, следствие. Доказать расходимость гармонического ряда.
|
|
|
а)Необходимый признак сходимости ряда, следствие.
Пусть ряд 
Доказательство.
1)
2) При 
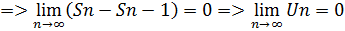
Замечание 1.
Если 
Замечание 2.
Если 
б)Доказать расходимость гармонического ряда.
Рассмотрим.
Находим последовательность частичных сумм
Вывод:Так как члены гармонического ряда либо больше, либо совпадают с соответствующими членами ряда вспомогат., то ряд расходящийся.
Функциональные ряды. Область сходимости. Степенные ряды, вычисление радиуса сходимости.
а)Функциональные ряды
Ряд называется функциональным если членом ряда является функция зависящая от x.
б)Область сходимости
Придавая x различные числовые значения, то получаем различные числовые ряды, которые могут быть сходящимися и расходящимися. Множество тех значений x при которых ряд сходится называется областью сходимости данного ряда.
Рассмотрим ряд:
q=x,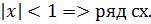 
т.е.(-1;1)-область сходимости ряда.
В область сходимости ряда сумма ряда - функция зависящая от x.
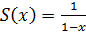
в)Степенные ряды, вычисление радиуса сходимости
|
|
|
1) 
2)При x=0=>ряд сх. ,S= 
3)(-R;R)-обл. сх. , где R= 
4)Если R=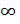 
=>( 
)
5)Если R=0 => ряд сх. в точке.
Ряд Тейлора, ряд Маклорена
а)Ряд Тейлора
Будем рассматривать сходящийся степенной ряд. По степеням (x-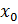 
) в области сходимости сумма ряда f(x)
f(x)= 
Найдем коэффициент разложения через значения функции и ее производных в точке :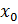
f( 
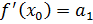
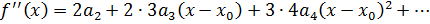
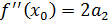
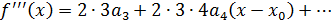
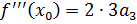
Найденные коэффициенты подставить в выражение:
б)Ряд Маклорена
Пусть 
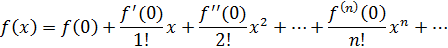
Разложение элементарных функций в ряд Маклорена
Найдем область сходимости:
R= 
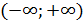=>ряд сх. для любого x
26)Разложение в ряд Маклорена функции: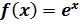 
, 
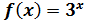
а)
Найдем область сходимости:
R=
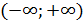=>ряд сх. для любого x
б) 
= 
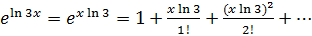
27)Разложение в ряд Маклорена функций: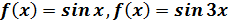 
а) 
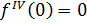
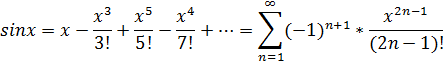
для любого х
б) 
= 
28)Разложение в ряд Маклорена функций: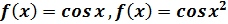 
а) 
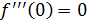
б) 
не обязательно
Дата добавления: 2018-08-06; просмотров: 285; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!