Касательная плоскость и нормаль поверхности.

⇐ ПредыдущаяСтр 3 из 3

Пусть в прямоугольной декартовой системе координат oxyzзаданна поверхность z=f(x,y). Возьмем на поверхности точку М и проведем через эту точку всевозможные кривые лежащие на поверхности к каждой из полученных кривых проведем касательные в точке М.

Касательной плоскостью к пов-ти z=f(x,y) в точке М наз плоскость в которой лежат все касательные проведенные к всевозможным кривым лежащим на поверхности и проходящей через точку М.

Нормалью к поверхности наз вектор ⊥ касательной плоскости в точке касания. Если пов-стьзадана уравнением z=f(x,y) то вектор нормали n имеет координаты n(∂z/∂х, ∂z/∂у, -1). Пусть точка М имеет координаты (x0,y0,z0) возьмем на касательной плоскости N с текущими координатами (x,y,z) тогда MN будет лежать на плоскости и он будет⊥вектору нормали n т.к. MN и n взаимно перпендикулярны

то их скалярное произведение равно нулю.(MN,n)=0

MN(x-x0,y-y0,z-z0) Подставив координаты в скалярное произведение получим: (∂z/∂х)(М)(х-х0)+(∂z/∂у)(М)(у-у0)=z-z0 уравнение описывает касательную плоскость проведенную к пов-ти z=f(x,y) в точке М(x0,y0,z0). Т.к. направляющий вектор совпадает с вектором n, то уравнение нормали имеет вид:(x-x0)/Zx1(M)=(y-y0)/ Zy1(M)=(z-z0)/-1

Если поверхность задана неявно уравнением F(x,y,z)=0, то уравнение касательной плоскости и нормали поверхности проведения в М(x0,y0,z0)

имеет вид: F1x(M)(x-x0)+ F1y(y-y0)+ F1x(M)(z-z0)=0

уравнение нормали:(x-x0)/Fx1(M)=(y-y0)/ Fy1(M)=(z-z0)/ FZ1(M).

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+Dх, у₀+Dу).

Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.

Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
Определение 7. Точка называется точкой минимума (максимума) функции 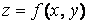, если существует такая окрестность точки , что для всех точек из этой окрестности выполняется неравенство , ().

Точки минимума и максимума функции 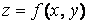называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).

Заметим, что минимум и максимум функции имеют локальный характер, так как значение функции в точке сравнивается с ее значениями в точках, достаточно близких к .

Теорема 1 (необходимые условия экстремума). Если точка экстремума дифференцируемой функции 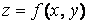, то ее частные производные и в этой точке равны нулю: .

Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция 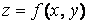может иметь экстремум, а может и не иметь.

Теорема 2 (достаточное условие экстремума). Пусть функция 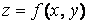: а) определена в некоторой окрестности критической точки , в которой и ; б) имеет непрерывные частные производные второго порядка . Тогда, если , то функция в точке имеет экстремум: максимум, если А<0; минимум, если А>0; если 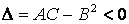, то функция в точке экстремума не имеет. В случае вопрос о наличии экстремума остается открытым.

Дата добавления: 2018-08-06; просмотров: 278; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!