Частная производная Геометрич. Смысл
Частной производной ф-ии Z=f(x,y) по переменной х наз-ся предел отношения частного приращения ф-ии по данной переменной к соответствующей приращению переменной когда последняя → 0 z|x= f|x= ∂z/∂x=∂f/∂x= lim(?х→0) ?хz /?х
Геометрический смысл ЧП-ой состоит в следующем : значение ЧП-ой по переменной «х» = тангенсу угла наклона на касательной проведённой к кривой получаемой пересечением поверхностей Z=f(x,y) и плоскости у=у0.Анологично опр-ся геометрический смысл ЧП-ой по переменной «у». Значение ЧП-ой по переменной «у» = тангенсу угла наклона касательной проведённой к кривой к-рая получается при пересечении поверхности с плоскостью х=х0
Частные производные высших порядков
Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют) 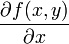 и
и 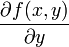 , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная
, которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная 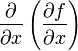 обозначается через
обозначается через 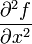 или
или 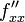 , а
, а 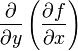 через
через 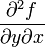 или
или 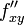 . Таким образом,
. Таким образом,
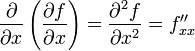 ,
, 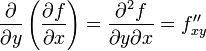
и, аналогично,
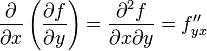 ,
, 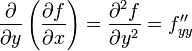 .
.
Теорема о равенстве производных
Частные производные одной и той же функции равны между собой, отличаются лишь порядком дифференцирования, если они непрерывны.
Полным дифференциалом функции 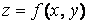 называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
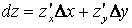 .
.
Учитывая, что дифференциалы независимых переменных совпадают с их приращениями, т.е. 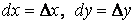 , формулу полного дифференциала можно записать в виде
, формулу полного дифференциала можно записать в виде
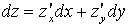 или
или 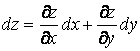 .
.
|
|
|
Частные производные неявной и сложной функции
Если в уравнении вида 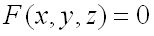 каждой паре чисел
каждой паре чисел 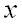 и
и 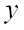 из некоторой области соответствует одно или несколько значений
из некоторой области соответствует одно или несколько значений 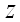 , удовлетворяющих этому уравнению, то уравнение
, удовлетворяющих этому уравнению, то уравнение 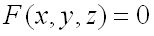 неявно определяет одну или несколько однозначных функций
неявно определяет одну или несколько однозначных функций 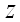 от
от 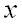 и
и 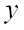 . В этом случае говорят, что
. В этом случае говорят, что 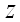 есть неявная функция от
есть неявная функция от 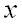 и
и 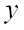 .
.
Частные производные 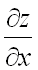 и
и 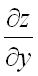 неявной функции находятся по формулам (предполагается, что
неявной функции находятся по формулам (предполагается, что 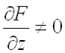 ):
):
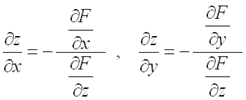 .
.
Скалярное поле
Если каждой точке Mобласти многомерного пространства поставлено в соответствие некоторое (обычно — действительное) число u, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая Rn в R (скалярная функция).
Производная по направлению
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
|
|
|
Рассмотрим функцию 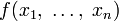 от
от 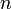 аргументов в окрестности точки
аргументов в окрестности точки 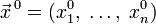 . Для любого единичного вектора
. Для любого единичного вектора 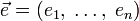 определим производную функции
определим производную функции 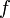 в точке
в точке 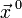 по направлению
по направлению  следующим образом:
следующим образом:
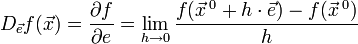
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора  .
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
[править]Связь с градиентом
Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
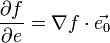 ,
,
где 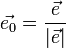 — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора  .
.
|
|
|
Градие́нт (от лат. gradiens, род.падеж gradientis — шагающий, растущий) — вектор, показывающий направление наискорейшего возрастания некоторой величины  , значение которой меняется от одной точки пространства к другой (скалярного поля).
, значение которой меняется от одной точки пространства к другой (скалярного поля).
Дата добавления: 2018-08-06; просмотров: 349; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
