Расчет пластинки методом конечных элементов

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Для многих задач теории упругости аналитических решений найти не удается. К таким задачам относится и расчет пластинки на упругом основании. Поэтому в последнее время широко используются численные методы, среди которых самым распространенным является метод конечных элементов – МКЭ.

Метод конечных элементов обычно используется для вариант перемещений, так как это упрощает алгоритмизацию, что очень важно при составлении прикладных программ. Метод конечных элементов реализуется в вариационной постановке.

(19)

где П – потенциальная энергия деформации;

W – работа внешних сил;

- вектор напряжений;

- вектор деформаций;

– вектор узловых сил;

- вектор узловых перемещений.

То есть, МКЭ является методом нахождения минимума функционала (19). Основная концепция МКЭ заключается в дискретизации пластинки, которая расчленяется сеткой на конечные элементы (рис. 8). На полученной дискретной модели вводятся кусочно-линейные функции , определенные на каждом конечном элементе. Такие функции называются координатными или аппроксимирующими. Искомая функция по области W, то есть в пределах одного конечного элемента, может быть записана для прямоугольного элемента в следующем виде

(20)

где L – общее количество степеней свободы, равное утроенному количеству узлов (равное 12 для прямоугольного КЭ);

- вектор узловых перемещений, который формируется из перемещений узлов конечного элемента (рис. 9).

Таким образом, задача определения непрерывной функции сводится к определению значений конечного числа перемещений узлов модели, которые находятся из условия минимума функционала (19), то есть из системы линейных алгебраических уравнений

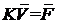, (21)

где , , K – вектор узловых перемещений, вектор узловых сил и матрица жесткости конечно-элементной модели.

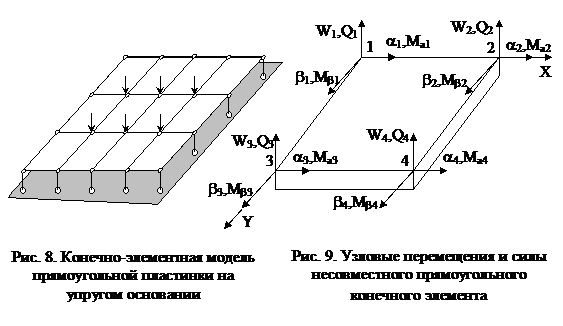
Для расчета прямоугольной плиты на упругом основании используются прямоугольные несовместные конечные элементы, имеющие четыре узла и двенадцать степеней свободы (рис. 9). Основание Фусса-Винклера моделируется упругими вертикальными стержнями, которые одним концом шарнирно прикрепляются к узлам модели плиты, а другим - к неподвижной опоре (рис.8). Жесткость этих стержней учитывается при формировании объединенной матрицы жесткости конечно-элементной системы.

Матрица жесткости K получается путем объединения матриц жесткости всех конечных элементов, составляющих численную модель. Для автоматизации объединения матриц жесткостей и векторов узловых сил в МКЭ используются три системы нумераций: нумерация конечных элементов; глобальная и местная нумерация узлов (рис. 10).

Матрица жесткости прямоугольного конечного элемента является квадратной и содержит 12 строк и 12 столбцов. При ее формировании для каждого конечного элемента предварительно строят геометрическую матрицу и матрицу физических коэффициентов, а затем их перемножают.

, (22)

где B – матрица геометрических параметров;

D – матрица физических коэффициентов

; ,

где h – толщина пластинки;

E – модуль упругости тела;

u - коэффициент Пуассона;

W – геометрическая функция, принятая для пластинки в виде (23):

(23)

где j_jw, j_j_a, j_j_b - функции, подбираемые в каждом отдельном случае по предполагаемой форме изгиба конечного элемента.

Матрица жесткости K в МКЭ является сильно разреженной, так как в каждой ее строке число ненулевых элементов очень мало и составляет менее одного процента от всех элементов строки. Поэтому в прикладных программах, реализующих метод конечных элементов, применяется специальная технология операций над такими сильно разреженными матрицами: хранение, сложение, умножение на вектор, вычеркивание строк и столбцов, факторизация (приведение к треугольному виду). Применение такой технологии позволяет уменьшить требуемые затраты памяти и сократить время решения задачи. Решение системы уравнений (21) дает вектор узловых перемещений . Используя принятые системы нумерации (рис. 10), из вектора выделяют вектора узловых перемещений для каждого конечного элемента, содержащегося в численной модели . Вектор напряжений в каждом конечном элементе вычисляется по формуле

. (24)

На кафедре «Сопротивление материалов и теория упругости» БНТУ разработана программа CROSS на ПЭВМ для расчета пластинки на упругом основании. Результаты расчета, полученные с помощью этой программы (табл. П3), использованы в качестве заданий для контрольной (расчетно-графической) работы по теории упругости.

Л и т е р а т у р а: [1, §8.1, §8.8- 8.10], [5, §2.1-2.3].

Дата добавления: 2018-08-06; просмотров: 359; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!