Напряженное состояние в точке
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Белорусский национальный технический университет
Кафедра “Сопротивление материалов и теория упругости”
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к контрольным (расчетно-графическим) работам по теории
упругости и пластичности для студентов специальностей
j-70 03 01 «Автомобильные дороги»
j-70 03 02 «Мосты, транспортные тоннели и метрополитены»
Минск 2003
УДК 539.3(075.8)
ББК 22.251 я7
Ш37
Методические указания содержат краткие сведения по некоторым разделам теории упругости - исследование напряженно-деформированного состояния в точке, изгиб пластинок на упругом основании, численные методы (МКЭ) решения задач теории упругости, а также контрольные задания, план решения и пример выполнения задания.
Методические указания предназначены для студентов специальностей «Дорожное строительство» и «Мосты, транспортные тоннели и метрополитены» очной и заочной форм обучения с целью восполнить недостаток этих сведений в учебной литературе по теории упругости и пластичности.
Составили:
Л.И.Шевчук, О.Л.Вербицкая, А.Е.Кончиц
ВВЕДЕНИЕ
Теория упругости и пластичности является одним из разделов механики твердого деформируемого тела и рассматривает задачи о действии сил (температуры) на упругое тело с целью определения возникающих при этом напряжений и деформаций. В отличие от сопротивления материалов в теории упругости используется более строгая постановка задач и применяются более точные методы их решения. Однако точная постановка задач и использование сложного математического аппарата не всегда позволяют получить решение в виде аналитического выражения (формулы) как это удается сделать в сопротивлении материалов. Поэтому в последнее время для решения задач теории упругости все чаще стали использоваться численные методы, позволяющие получать решения для многих задач, имеющих большое практическое значения. Это задачи на контактные напряжения, расчет балки-стенки, пластинок и оболочек различных геометрических форм, пространственных тел и др.
|
|
|
В методических указаниях предлагается задача по расчету прямоугольной пластинки (плиты) на упругом основании методом конечных элементов.
Даны краткие пояснения по исследованию напряженно-деформированного состояния в точке тела, по теории изгиба тонких пластин, по технологии метода конечных элементов, приведены данные к заданию и пример.
Методические указания составлены в соответствии с учебной программой дисциплины «Теория упругости и пластичности», утвержденной Советом Белорусского национального технического университета (протокол № 5 от 26 апреля 2002 г).
|
|
|
Указания по выполнению контрольной
Расчетно-графической) работы
Для студентов очной формы обучения числовые данные к расчетно-графической работе задаются преподавателем. Числовые данные задания к контрольной работе студента заочной формы обучения определяются тремя последними цифрами личного номера (шифра) студента и первыми тремя буквами русского алфавита, которые располагаются под шифром. Цифры, обозначающие год поступления в институт, не используются. Если личный номер состоит из менее чем трех цифр, впереди дописываются нули.
| Например: | 78-832 | 76-12 | à | 76-012 | |
| абв | абв |
В первом случае а = 8, б = 3, в = 2, а во втором – а = 0, б = 1, в = 2.
Числовые данные берутся из таблиц П1 и П2 в зависимости от связи цифры с буквой, написанной под ней (например: 8а, 3б, 2в). Так для шифра 76-832 из таблицы П1 и П2 следует взять следующие данные
E=14 МПа; t=32 см; F=550 кН
и принять точки приложения сил F, обозначенные на схеме номерами, соответственно, 1, 2, 5, 7. Погонные изгибающие и крутящий моменты, взять из таблицы П3 Работа, выполненная с нарушениями этих требований, не рецензируется.
|
|
|
В заголовке контрольной (расчетно-графической) работы должны быть четко указаны: наименование высшего учебного заведения, название дисциплины, фамилия, имя и отчество студента, номер группы, для студентов заочной формы обучения – личный номер (шифр) и точный домашний адрес. Работа должна быть аккуратно оформлена на листах формата А4. Для студентов заочной формы обучения допускается оформление контрольной работы в тетради. Чертежи и рисунки выполняются карандашом 2B, шариковой ручкой с черной пастой или тушью. Допускается использование машинной графики. Содержание и последовательность выполнения задания изложены в методических указаниях и в примере.
При исправлении ошибок в работе сделанные рецензентом замечания сохраняются. Контрольная (расчетно-графическая) работа будет зачтена только после опроса студента.
Для выполнения контрольной (расчетно-графической) работы предварительно требуется изучить следующие темы из курса теории упругости: теория напряженно-деформированного состояния в точке, изгиб пластин, численные методы решения задач линейной теории упругости (метод конечных элементов), теории прочности.
|
|
|
Напряженное состояние в точке
В механике твердого деформированного тела различают внешние и внутренние силы. Внешние силы – это силы взаимодействия между отдельными телами. Внутренние силы – это силы взаимодействия между частями одного тела (элемента конструкции). Интенсивность внутренних сил измеряется напряжениями: полным, нормальным и касательным. В методических указаниях приняты следующие обозначения и знаки напряжений.
Нормальное напряжение обозначается буквой s и имеет один индекс, совпадающий с обозначением той оси, параллельно которой направлено напряжение (sx, sy, sz). Нормальное напряжение считается положительным, если оно вызывает растяжение.
Касательное напряжение обозначается буквой t и имеет два индекса. Первый индекс совпадает с обозначением оси, параллельно которой направлено напряжение, а второй – совпадает с обозначением оси, которая является нормалью к площадке, где действует напряжение (txy, tyz, tzx). Касательное напряжение считается положительным, если его направление и направление внешней нормали площадки, к которой оно приложено, одновременно совпадают или одновременно не совпадают с положительными направлениями соответствующих координатных осей.
Напряженное состояние в точке тела полностью определяется тензором напряжений Ts ,представляющим собой квадратную матрицу, содержащую напряжения, расположенные в строго определенном порядке.
(1)
В соответствии с законом парности касательных напряжений
txy = tyx; tyz =tzy; tzx = txz тензор напряжений всегда симметричная матрица.
Через элементарную площадку, проведенную вблизи точки тела, передается внутренняя сила, характеризуемая полным напряжением pu , которое может быть разложено на нормальную su и касательную
tu составляющие (рис. 2). Положение наклонной площадки определяется направляющими косинусами ее внешней нормали u
l = cos(x, u); m = cos(y, u); n = cos(z, u). (2)
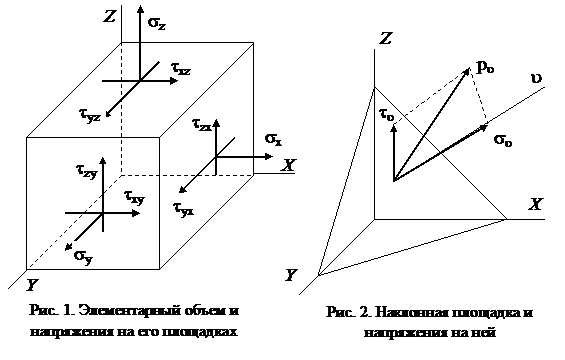
Из условия равновесия элементарного объема в форме тетраэдра (рис.2) можно получить зависимость проекций полного напряжения и напряжений, действующих на координатных площадках:
pxu = sxl + txym + txzn,
pyu = tyxl +sym + tyzn, (3)
pzu = tzxl + tzym + szn.
Эти уравнения называют граничными условиями или условиями на поверхности тела, так как их левые части могут рассматриваться и как проекции интенсивности нагрузки, приложенной к поверхности тела. Из курса сопротивления материалов известно, что всегда около некоторой точки тела можно найти три взаимно перпендикулярных площадки, на которых касательные напряжения равны нулю, а нормальные принимают экстремальные значения. Такие площадки и нормальные напряжения, действующие на них, называются главными. Если наклонная площадка (рис.2) главная, то tu = 0, а pu = su. Согласно уравнениям (3) имеем
pxu = pul = sul = sxl + txym + txzn,
pyu = pum = sum = tyxl + sym + tyzn, (4)
pzu = pun = sun = tzxl + tzym + szn.
Отсюда следует
(sx-su)l + txym + txzn = 0,
tyxl + (sy-su)m + tyzn = 0, (5)
tzxl + tzym + (sz-su)n = 0.
Система однородных уравнений (5) имеет нулевое решение (l=0, m=0, n=0, su=0). Но условие l2 + m2 + n2 =1 требует, чтобы система имела и ненулевые решения, а это возможно, если определитель будет равен нулю.
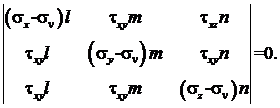 (6)
(6)
Для удобства записи опустим индекс u, развернем определитель (6) и получим кубическое уравнение следующего вида
s3 - sI s2 + sIIs - sIII = 0. (7)
Корни кубического уравнения (7) и являются значениями главных напряжений, которые обозначаются согласно условию
s1³ s2 ³ s3.
Положение главных площадок, то есть их направляющие косинусы определяются решением системы уравнений (5).
Коэффициенты sI , sII , sIII кубического уравнения (7) не зависят от выбранной системы координатных осей и называются инвариантами тензора напряжений. Они могут быть выражены через элементы тензора напряжений следующим образом
sI = sx + sy + sz ;
sII = sx sy + sy sz + sz sx - txytyx - tyztzy - tzxtxz;
sIII = sx sy sz + 2txytyztzx - tyxsxtxy- tzysytyz- txzsxtzx. (8)
В теории упругости выделяются еще и другие особенные площадки и напряжения. Площадки, равно наклоненные к направлениям главных напряжений, называются октаэдрическими площадками. Около точки тела можно провести восемь октаэдрических площадок, которые вместе образуют объемное тело, называемое октаэдром. Нормальные и касательные напряжения, действующие на этих площадках, являются также инвариантами и называются октаэдрическими напряжениями. Они могут быть выражены через главные напряжения.
, (9)
где sm – среднее напряжение
(10)
В некоторых случаях при проверке наступления предельного состояния в опасной точке конструкции используется, так называемая, интенсивность напряжения, которая является инвариантой и выражается через октаэдрическое напряжение следующим образом:
. (11)
Л и т е р а т у р а: [1, §1.1, 1.2, §6.1-6.6], [2, §1.1, 1.2, §1.4-1.6, §III-4], [3, §2.01, §2.04-2.07, §2.09], [4, §1.1, §1.3, §1.4].
Дата добавления: 2018-08-06; просмотров: 738; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
