Метод конфигураций (метод Хука и Дживса)
Алгоритм включает в себя два основных этапа поиска.

а) В начале обследуется окрестность выбранной точки (базисной точки), в результате находится приемлемое направление спуска; б) Затем в этом направлении находится точка с наименьшим значением целевой функции. Таким образом находится новая базисная точка.
 |
Эта процедура продолжается пока в окрестностях базисных точек удается находить приемлемые направления спуска.
Схема алгоритма
Шаг 1. Задаются начальное приближение (первая базисная точка)
 ,
,
начальный шаг h для поиска направления спуска, точность решения d(предельное значение для шага h). Присваивается к=0.
Шаг 2. (Первый этап).
Определяется направление минимизации целевой функции
 f(x)=f(x(1),x(2),…,x(n)) в базисной точке
f(x)=f(x(1),x(2),…,x(n)) в базисной точке
. Для этого последовательно дают приращение переменным x(j) в точке хк. Присвоим z=xk. Циклически даем приращение переменным x(j) и формируем z(j)=xk(j)+h, если f(z)<f(xk), если же нет, то z(j)=xk(j)-h, если f(z)<f(xk), иначе z(j)=xk(j). Так для всех j(j=1,2,…,n).
Шаг 3. Если z=xk, то есть не определилось подходящее направление, то обследование окрестности базисной точки хк повторяется, но с меньшим шагом h (например, h=h/2).
Если h>d, то перейти к шагу 2, то есть повторить обследование точки хк.
Если h£d, то поиск заканчивается, то есть достигнуто предельное значение для шага h и найти приемлемое направление спуска не удается. В этом случае полагается
|
|
|
Шаг 4. (Второй этап).
 Если z¹xk, то требуется найти новую базисную точку в направлении
Если z¹xk, то требуется найти новую базисную точку в направлении
вектора z-xk: xk+1=xk + l(z-xk), где l - коэффициент «ускорения поиска».
Определяется такое значение l=lк, при котором достигается наименьшее значение целевой функции в выбранном направлении, то есть функции
f(xk +l(z-xk) = j(l).
В зависимости от способа выбора lк возможны варианты метода:
а) lк=l=const постоянная для всех итераций; б) задается начальное l0=l, а далее lк=lк-1, если f(xk+1)<f(xk), иначе дробим lк, пока не выполнится это условие; в) lк определяется решением задачи одномерной минимизации функции j(l).
Таким образом определяется новая базисная точка xk+1=xk + l(z-xk). Полагаем к=к+1 и поиск оптимального решения повторяется с шага 2.
Метод симплекса
Под симплексом понимается n-мерный выпуклый многогранник n-мерного пространства, имеющий n+1 вершину. Для n=2 это треугольник, а при n=3 это тетраэдр.
Идея метода состоит в сравнении значений функции в n+1 вершинах симплекса и перемещении симплекса в направлении лучшей точки. В рассматриваемом методе симплекс перемещается с помощью операций отражения. Далее принято следующее: х0(k), х1(k), … , хn(k) – вершины симплекса, где к - номер итерации.
|
|
|
| |
Шаг 1. Построение начального симплекса.
Для этого задаются начальная точка х0(0) и длина ребра симплекса l. Формируются остальные вершины симплекса:
xi(0) = x0(0) + l*ei (i=1,2,…,n), где ei – единичные векторы.
Шаг 2. Определение направления улучшения решения.
Для этого на к-й итерации вычисляются значения целевой функции в каждой точке симплекса. Пусть для всех i: f(xmin(k))£f(xi(k))£f(xmax(k)), где min, max, i – номера соответствующих вершин симплекса. Опр–м центр тяжести всех точек, исключая точку xmax(k), Ck=(Sxi(k))/n .
Тогда направление улучшения решения опр–ся вектором Ck-xmax(k).
Шаг 3. Построение отраженной точки.
Замена вершины xmax(k) с максимальным значением целевой функции на новую точку с помощью операции отражения, результатом которой является новая точка:
uk=ck+(ck-xmax(k))=2ck-xmax(k)
| |
Вычисляем f(uk). При этом возможен один из двух случаев:
а) f(uk)<f(xmax(k); б) f(uk)³f(xmax(k).
Случай а): вершина xmax заменяется на uk, чем определяется набор вершин к+1-й итерации и к-я итерация заканчивается.
Случай б): в результате отражения получается новая точка uk, значение функции в которой еще хуже, чем в точке xmax, то есть отражать симплекс некуда. Поэтому в этом случае производится пропорциональное уменьшение симплекса (например, в 2 раза) в сторону вершины xmin(k): xi(k+1)=x^i=(xi(k)+xmin(k))/2, где i=0,1,…,n.
|
|
|
На этом к-я итерация заканчивается.
Шаг 5. Проверка сходимости.
Если
то поиск минимума заканчивается и полагается
В противном случае к=к+1 и происходит переход к шагу 2.
Метод деформируемого симплекса (метод Нелдера – Мида)
 |
Метод деформируемого симплекса обладает большей общностью и позволяет учитывать локальные свойства поверхности целевой функции. Симплексы вытягиваются в направлении наклона поверхности, их оси поворачиваются при встрече с оврагом на поверхности целевой функции, вблизи минимума они сжимаются.
 |
В рассматриваемом методе симплекс перемещается с помощью трех основных операций над симплексом: отражение, растяжение и сжатие.
Схема алгоритма.
Шаг 1. Построение начального симплекса.
Задаются начальная точка х0(0) и длина ребра l. Формируются остальные вершины симплекса: xi(0)=x0(0)+lei (i=1,2,…,n), где ei – единичные векторы.
Шаг 2. Определение направления улучшения решения.
|
|
|
Для этого на каждой итерации вычисляются значения целевой функции в каждой вершине симплекса. Пусть для всех i
f(xmin(k))≤ f(xi(k)) ≤ f(xm(k)) ≤ f(xmax(k)),
где min, m, max, i-номера соответствующих вершин симплекса. Определим центр тяжести всех точек, исключая точку xmax(k), 
Тогда направление улучшения решения определяется векторов Ck- xmax(k).
Шаг 3. Построение нового симплекса.
Замена вершины xmax(k) с максимальным значением целевой функции на новую точку с помощью операции отражения, результат которой является новая точка
uk=Ck+a*(Ck-xmax(k)), где a-коэффициент отражения.
Шаг 4. Построение нового симплекса.
Вычисляем f(uk), при этом возможно один из трех случаев:
а) f(uk)< f(xmin(k));
б) f(uk)>f(xm(k));
в) f(xmin(k))≤ f(uk) ≤ f(xm(k));
Случай а): отражённая точка является точкой с наилучшим значением целевой функции. Поэтому направление отражение является перспективным и можно попытаться растянуть симплекс в этом направлении. Для этого строиться точка
Vk= Ck+b*(uk-Ck), где b>1 –коэффициент расширения.
Если f(vk)<f(uk), то вершина xmax(k) заменяется на vk, в противном случае на uk и k-ая итерация заканчивается.
Случай б): в результате отражения получается новая точка uk, которая, если заменить xmax(k), сама станет наихудшей. Поэтому в этом случае производится сжатие симплекса. Для этого строится точка vk:

где 0<g<1 –коэффициент сжатия.
Если f(vk)<min{f(xmax(k)),f(uk)}, то вершина xmax(k) заменяется на vk .
В противном случае вершинам xi(k+1) (i=0,1,2,..,n) присваивается значение:
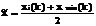 |
и на этом k-ая итерация заканчивается.
в) вершина xmax(k) заменяется на uk, чем определяется набор вершин k+1-й итерации и k –ая итерация заканчивается.
Шаг 5.
Проверка сходимости. Если
то поиск минимума заканчивается и полагается
 |
В противном случае к=к+1 и происходит переход к шагу 2.
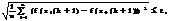 |
Опыт использования описанного алгоритма показывает, что целесообразно брать следующие значения параметров: a=1, b=2, g=0.5.
Метод Ньютона
В методе Ньютона последовательность точек спуска определяется формулой (4). Для текущей точки xk направление и величина спуска определяется вектором pk = – (f ''(xk)) –1·f '(xk). Хотя в определении вектора pk фигурирует обратная к f ''(xk) матрица (f ''(xk)) –1, на практике нет необходимости вычислять последнюю, так как направление спуска pk можно найти как решение системы линейных уравнений
f ''(xk)·pk = – f '(xk) (5) каким-нибудь из методов.
Схема алгоритма.
| шаг 1: | На первой итерации, при k = 0, вводятся начальное приближение x0 и условие останова ε3. Вычисляются градиент f '(x0) и матрица f ''(x0). | ||||
| шаг 2: | Определяется направление спуска pk, как решение системы линейных уравнений f ''(xk)·pk = – f '(xk) ( например, методом исключений Гаусса). | ||||
| шаг 3: | Определяется следующая точка спуска:xk+1 = xk + pk. | ||||
| шаг 4: | Вычисляются в этой точке xk+1 градиент f '(xk+1) и матрица f ''(xk+1). | ||||
| Если ||f '(xk+1)|| £ ε3, то поиск на этом заканчивается и полагается x = xk+1 и y = f(xk+1). Иначе k = k + 1 и переход к шагу 2. |
Особенностью метода Ньютона является то, что для квадратичной целевой функции он находит минимум за один шаг, независимо от начального приближения x0 и степени овражности.
В общем случае, когда минимизируемая функция не квадратична, вектор pk = – (f ''(xk)) –1·f '(xk) не указывает в точку её минимума, однако имеет большую составляющую вдоль оси оврага и значительно ближе к направлению на минимум, чем антиградиент. Этим и объясняется более высокая сходимость метода Ньютона по сравнению с градиентными методами при минимизации овражных целевых функций.
Недостатками метода Ньютона является то, что он, во-первых, предполагает вычисление вторых производных и, во-вторых, может расходиться, если начальное приближение находится слишком далеко от минимума.
Методы с регулировкой шага (методы Ньютона – Рафсона)
Удачный выбор начального приближения x0 гарантирует сходимость метода Ньютона. Однако отыскание подходящего начального приближения – далеко не простая задача. Поэтому необходимо как-то изменить формулу (4), чтобы добиться сходимости независимо от начального приближения. Доказано, что в некоторых предположениях для этого достаточно в методе Ньютона кроме направления движения (f ''(x)) –1·f '(x) выбирать и длину шага вдоль него. Такие алгоритмы называются методами Ньютона с регулировкой шага (методами Ньютона – Рафсона) и выглядят так:
xk+1 = xk – ak(f ''(xk)) –1·f '(xk). (6)
Как и в градиентных методах величина ak выбирается так, чтобы обеспечить убывание целевой функции на каждой итерации. Мы рассмотрим два способа выбора шага ak. Первый из них связан с проверкой неравенства
f(xk + akpk ) – f(xk) £ d·ak(f '(xk), pk), (7)
где pk = – (f ''(xk)) –1·f '(xk) – направление спуска, а 0 < d < ½ – некоторое заданное число, общее для всех итераций. Если это неравенство выполнено при ak = 1, то шаг принимается равным единице и осуществляется следующая итерация. Если нет – дробится до тех пор, пока оно не выполнится.
Схема метода Ньютона – Рафсона с дроблением шага.
| шаг 1: | На первой итерации, при k = 0, вводятся исходные данные x0, d, ε3. Вычисляются значения градиента f '(x0) и матрица f ''(x0). | ||||
| шаг 2: | Присваивается a = 1. Определяется направление спуска pk, как решение системы линейных уравнений f ''(xk)·pk = – f '(xk). | ||||
| шаг 3: | Проверяется условие f(xk + akpk ) – f(xk) £ d·ak(f '(xk), pk). Если выполняется, то переход к шагу 4.Иначе дробим значение шага a (например, a = a/2) и повторяем шаг 3. | ||||
| шаг 4: | Определяется следующая точка: xk+1 = xk + a·pk. | ||||
| Вычисляются значение градиента f '(xk+1) в точке xk+1. | ||||
| шаг 6: | Если ||f '(xk+1)|| £ ε3, то поиск на этом заканчивается и полагается x = xk+1 и y = f(xk+1). Иначе k = k + 1 и переход к шагу 2. |
Второй метод определения шага ak в схеме (6), как и в методе наискорейшего спуска состоит в минимизации функции
f(xk + akpk ) = min f(xk + akpk ).
Схема метода Ньютона – Рафсона с выбором оптимального шага. α≥0
| шаг 1: | При k = 0, вводятся x0, ε3. Вычисляются f '(x0) и f ''(x0). | ||||
| шаг 2: | Определение направления спуска pk, как решение системы линейных уравнений f ''(xk)·pk = – f '(xk). | ||||
| Определяется следующая точка спуска: xk+1 = xk + apk, где a - решение задачи одномерной оптимизации: min f(xk + apk ). | ||||
| шаг 4: | Вычисляются в точке xk+1: f '(xk+1) и f ''(xk+1). | ||||
| Если ||f '(xk+1)|| £ ε3, то поиск заканчивается и полагается x = xk+1 и y = f(xk+1). α≥0 Иначе k = k + 1 и переход к шагу 2. |
Модификации метода Ньютона
Значительные трудности, возникающие при практической реализации метода Ньютона, связаны с необходимостью вычислить матрицу f ''(x). Мы рассмотрим две модификации метода Ньютона, которые используют не точные значения, а некоторые приближённые аналоги матрицы вторых производных. В результате уменьшается трудоёмкость методов, но, конечно, ухудшается их сходимость.
В качестве первой модификации метода Ньютона рассмотрим следующий алгоритм:
xk+1 = xk – ak(f ''(xk)) –1·f '(xk), ak ≥ 0. (8)
здесь для построения направления спуска используется один раз вычисленная и обращённая матрица вторых производных f ''(x0).
Схема модификации I метода Ньютона.
| шаг 1: | При k = 0, вводятся x0, ε3. Вычисляются f '(x0) и f ''(x0). | ||||
| шаг 2: | Определение обратной матрицы (f ''(x0))–1. | ||||
| шаг 3: | Определение направления спуска pk:pk = – f '(xk)·(f ''(x0))–1. | ||||
| шаг 4: | Определение следующей точки: xk+1 = xk + a·pk, где a – решение задачи одномерной минимизации функции φ(a) = f(xk + a·pk), при a ≥ 0. | ||||
| Вычисление в точке xk+1.градиента f '(xk+1) | ||||
| шаг 6: | Если ||f '(xk+1)|| £ ε3, то поиск заканчивается и полагается x = xk+1 и y = f(xk+1). Иначе k = k + 1 и переход к шагу 3. |
В рассмотренной схеме для выбора шага ak используется способ аналогичный исп–му в методе наискорейшего спуска. Но можно было бы воспользоваться и способом аналогичным используемому в градиентном методе с дроблением шага.
Если матрица f ''(x) положительно определена, то итерационный процесс (d) является одной одной из модификаций градиентного спуска, независимо от начального приближения x0.
Дата добавления: 2018-08-06; просмотров: 619; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
