Градиентный метод с постоянным шагом
Алгоритм пассивного поиска минимума Отрезок [a,b] исходный отрезок неопределенности. Пусть N - число точек, в которых необходимо провести вычисления целевой функции f(x), т.е. N экспериментов. Точки, в которых необходимо провести эксперименты, определяются следующим образом: Среди вычисленных значений {f(xi)} (i=1,N), ищется точка xj , в которой достигается минимум: f(xj)= min f(xi) 1£i£N Найденная точка принимается за приближенное решение задачи . Исходный отрезок неопределенности [a,b] после экспериментов в N точках сужается до [xj-1,xj+1], длина которого равна: Точность найденного решения равна половине отрезка неопределенности, т.е. , где и x* - точное решение.
Алгоритм равномерного блочного поиска
Схема алгоритма
Шаг 1. Задаются исходный отрезок неопределенности [a,b], e - точность приближенного решения 
, число экспериментов в блоке – n (нечетное, n=2k-1). Проводим эксперимент в середине отрезка [a,b], т.е. вычисляем yk=f(xk), где xk=(a+b)/2.
Шаг 2. Проводим эксперименты в остальных точках блока: yi=f(xi), где xi=a+i*(b-a)/(n+1), i=1,2,..,n, i¹k. Находим точку xj, в которой достигается минимум среди вычисленных значений: f(xj)=min f(xi), следовательно, точное значение минимума x* содержится на отрезке [xj-1,xj+1].
Шаг 3. Полагаем a=xj-1, b=xj+1, xk=xj, yk=yj. Если b-a£2e, то 
, 
и поиск заканчивается. Иначе перейти к шагу 2. Если заданная точность e достигнута после т итераций, т.е. после экспериментов в m блоках, то длина отрезка неопределенности после всех N вычислений (N=n+(m-1)(n-1)=(n-1)m+1) будет:
|
|
|
и 
Алгоритм деления интервала пополам
Это вариант предыдущего алгоритма при n=3.
Схема алгоритма.
Шаг 1. Задаются a,b,e. Производим эксперимент в точке x2=(a+b)/2, т.е. вычисляем y2=f(x2).
Шаг 2. Проводим эксперименты в остальных точках блока: x1=(a+x2)/2, y1=f(x1), x3=(x2+b)/2, y3=f(x3).
Находим xj такую, что f(xj)=min {f(xi)}.
1 ≤ i ≤ 3 Тогда точное решение x* содержится на отрезке [xj-1,xj+1]. Предполагается 
.
Шаг 3. Полагаем a=xj-1, b=xj+1, x2=xj, y2=yj. Если b-a£2e, то 
и поиск заканчивается. Иначе перейти к шагу 2.
После к итераций общее число проведенных экспериментов равно N=2к+1, а длина получившегося отрезка неопределенности будет 
, где [z] – целая часть числа z. Следовательно, достигнутая точность будет 
, e=1/2LN.
Метод дихотомии
Это алгоритм блочного поиска для ni=n=2, т.е. когда в блоке два эксперимента. Так как пассивная составляющая алгоритма, т.е. блок, содержит четное число экспериментов, то оптимальный выбор точек xij, в которых необходимо провести эксперименты, будет неравномерным, в отличие от предыдущих алгоритмов, где число экспериментов в блоке было нечетным и, соответственно, расположение точек равномерным. Если блок содержит два эксперимента, то оптимальное (дельта оптимальное) расположение точек, в которых будут проводится эксперименты, это как можно ближе к середине отрезка. Такое расположение точек позволяет получить наименьший отрезок неопределенностей после экспериментов в блоке.
|
|
|
Схема алгоритма.
Шаг 1. Задаются a,b,e и d - малое положительное число, значительно меньшее чем e.
Шаг 2. Определяется середина отрезка x=(a+b)/2. Производятся эксперименты в двух точках близких середине: y1=f(x-d), y2=f(x+d).
Шаг 3. Определяется следующий отрезок локализации, т.е. определяется какой из отрезков [a,x+d] или [x-d,b] содержит точное решение x*. Если y1£y2, то это отрезок [a,x+d] и b=x+d, иначе это отрезок [x-d,b] и a=x-d, т.е. выбранный отрезок локализации мы снова обозначили как [a,b].
Шаг 4. Если b-a£2e, то x=(a+b)/2, 
и поиск заканчивается. Иначе перейти к шагу 2.
После к итераций общее число экспериментов будет N=2к, а длина получившегося отрезка неопределенности 
. Следовательно, 
.ъ
Метод золотого сечения
Для того чтобы уменьшить отрезок неопределённости [a,b], нам необходимо вычислить значение целевой функции f(x), по крайней мере, в двух точках на отрезке [a,b].
В результате этих двух экспериментов отрезок неопределённости сузится до отрезка [a,x2] или [x1,b]. Так как у нас нет никаких оснований предпочесть один из этих вариантов, то точки x1 и x2 должны быть симметричны относительно середины отрезка [a,b]. В этом случае длины отрезков [a,x2] и [x1,b] будут равны. Таким образом, остаётся вопрос как выбрать точку x1.
|
|
|
В методе золотого сечения точка x1 выбирается из соображения, что должно выполняться соотношение:
т.е. точка x1 делит отрезок [a,b] по правилу «золотого сечения», где λ - есть «золотое отношение». Точка x2 определяется как точка симметричная к x1 относительно середины отрезка.
В результате экспериментов у нас получается отрезок неопределённости [a,x2], содержащий точку x1, или отрезок неопределённости [x1б], содержащий точку x2. Оказывается, что остающаяся точка на суженном отрезке неопределённости делит его вновь по правилу «золотого сечения». Следовательно, чтобы, в свою очередь, уменьшить новый отрезок неопределённости, нам не достаёт одного эксперимента, а именно, вычисления целевой функции в точке, симметричной к оставшейся точке относительно середины этого нового отрезка. Всё продемонстрировано на рисунке,
а)
б)
где буквы со штрихами обозначают новый отрезок неопределённости. Вариант а) соответствует случаю, если новым отрезком неопределённости будет [a,x2], а вариант б) – отрезку [x1,b].
|
|
|
В приводимой ниже схеме алгоритма остающиеся отрезки неопределённости переименовываются каждый раз как [a,b], а точки, в которых проводятся эксперименты на этом отрезке, обозначается через x1 и x2, причём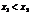 
. Кроме того, y1 и y2 имеют следующие значения: y1 =f(x1) и y2 =f(x2).
Схема алгоритма
Шаг1. Задаются a,b,ε и λ=1.618… Вычисляют 
.
Шаг2. а) Если 
, то полагают 
и вычисляют 
.
б) Если y1>y2, то полагают 
и вычисляют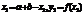 
.
Шаг3. Если b-a>ε, то переходят к шагу 2. Иначе если y1<y2, то полагают 
и 
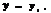если y1≥y2, то полагают 
и 
Закончить поиск.
После каждой итерации длина отрезка неопределённости уменьшается в λ раз. Так как первая итерация начинается после двух экспериментов, то после N экспериментов длина отрезка неопределённости будет 
.
Метод чисел Фибоначчи
Этот метод применяется, когда число экспериментов N заранее задано. Метод чисел Фибоначчи, также как и метод золотого сечения относится к симметричным методам, т.е. точки, в которых выполняются два эксперимента, на основе которых происходит уменьшение отрезка неопределённости, расположены симметрично относительно середины отрезка. Вот только выбор точки x1 происходит на основе других соотношений. Для этого используются числа Фибоначчи: 
, где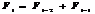 
и F0=F1=1.Точка x1 определяется из соотношения:
т.е.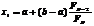 
. Точка x1 делит [a,b] на две неравные части. Отношение малого отрезка к большему равно 
. Точка x2 определяется как точка, симметричная к x1 относительно середины отрезка [a,b]. Поэтому 
. При этом будет выполняться условие x1<x2.
В результате экспериментов в точках x1 и x2 у нас получится отрезок неопределённости [a,x2], содержащий точку x1, или отрезок неопределённости [x1,b], содержащий точку x2. Остающаяся точка делит новый отрезок неопределённости на две неравные части в отношении:
. То есть в методе Фибоначчи остающаяся точка делит отрезок на две неравные части в пропорциях определяемых числами Фибоначчи. Так на к-ом шаге это отношение равно 
а длины отрезков равны: 
и 
. Всё это показано на рисунке:
а)
б)
Для того чтобы в свою очередь уменьшить получившийся отрезок неопределённости, надо определить симметричную точку относительно середины отрезка и произвести эксперимент в ней. Этот процесс продолжается, пока не будет проведено N экспериментов.
Схема алгоритма
Шаг 1. Задаются a,b,N Вычисляются числа Фибоначчи 
. Определяется:
Шаг 2. а) Если y1≤y2, то полагают 
и вычисляют 
.
б) Если y1>y2, то полагают 
и вычисляют 
.
Повторить шаг 2 N-2 раза.
Шаг 3. Если y1<y2, то полагают 
и 
. Если y1≥y2, то полагают 
и 
.
Закончить поиск.
Длина отрезка неопределённости в методе Фибоначчи 
.
Метод касательных
Пусть функция f(x) выпукла и дифференцируема на [a,b]. Идея метода состоит в следующем. Пусть [a,b] - отрезок неопределённости и 
- результаты вычислений в точках a и b. По этой информации строится аппроксимирующая функция, представляющую из себя кусочно-линейную функцию, состоящую из касательной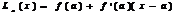 
к f(x) в точке a и касательной 
к f(x) в точке b.
Полученная аппроксимирующая функция есть ломанная состоящая из прямой La(x) на [a,c] и Lb(x) на [c,b], где с – точка пересечения касательных. Легко заметить, что при f(a)>0 и f(b)>0 минимум аппроксимирующей функции достигается в точке с. Значение точки пересечения с можно определить по формуле
В точке с производятся вычисления f(c) и f``(c). Если f``(c)=0, то решением задачи будет x*=c. Если же f `(c)>0, то в качестве следующего отрезка неопределённости будет [a,c]. Если же f``(c)<0, то – отрезок [c,b]. Процесс повторяется до тех пор, пока f `(c)=0 или отр–к неопр–ти не достигнет заданной точности.
Схема алгоритма:
Шаг 1. Заданы a,b,ε. Вычислить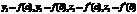 
.
Шаг 2. Если b-a≤2ε, то полагаем 
. Поиск окончен. Если b-a>2ε, то вычислить 
. Если z=0, то полагаем 
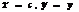и поиск окончен. Если z<0, то 
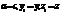. Если z>0, то 
. Повт–ть шаг2 .
Метод парабол
 |
Рассмотрим алгоритм квадратичной интерполяции или метод парабол, т.е. в качестве аппроксимирующей функции используется парабола. Для однозначного задания параболы необходимы три точки. Пусть имеются три точки, для кот–х вып–ся a<c<b, f(c)£f(a), f(c)£f(b). Так как [a,b] – отрезок неопределенности и f(x) – унимодальная функция, то найти такую точку c нетрудно. Парабола, проходящая через три точки (a,f(a)), (c,f(c)),(b,f(b)), имеет вид
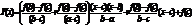
Поскольку f – унимодальная функция, то хотя бы одно из неравенств f(c)£f(a), f(c)£f(b) строгое и, следовательно, коэф–т при старшем члене P(x) положителен. Тогда P(x) достигает минимума в точке
,
причем (a+c)/2£t£(c+b)/2. Эта точка и выбирается в качестве точки очередного вычисления знач–я функции.
Если оказалось, что t=c, условимся в качестве точки очередного вычисления выбирать точку (a+c)/2. Итак, следующее вычисление проводится в точке
Определим новый отрезок неопределенности с лежащей внутри него точкой, для которой выполняются условия аналогичные условиям, которым удовлетворяла точка c. В силу унимодальности функции f и в зависимости от выполнения или невыполнения условий x<c, f(x)<f(c), f(x)=f(c)это будут отрезки с точкой внутри: [a,c] и x; [x,b] и c; [x,c] и (x+c)/2; [a,x] и c; [c,b] и x; [c,x] и (x+c)/2. Смотри рисунок. Далее строится парабола, определяется ее минимум, и т.д., до тех пор, пока длина отрезка неопределенности не удовлетворяет заданной точности.
Схема алгоритма:
 |
Шаг 1. Задаются a,c,b и e. Вычислить ya=f(a), yc=f(c), yb=f(b).
Шаг 2. Вычислить , y=f(x), где
Шаг 3. А) При x<c.
Если y<yc, то b=c, c=x, yb=yc, yc=y.
Если y>yc, то a=x, ya=y.
Если y=yc, то a=x, b=c, c=(x+c)/2, ya=y, yb=yc, yc=f(c).
Б) При x>c.
Если y<yc, то a=c, c=x, ya=yc, yc=y.
Если y>yc, то b=x, yb=y.
Если y=yc, то a=c, b=x, c=(x+c)/2, ya=yc, yb=y, yc=f(c).
Шаг 4. Если b-a£e, то закончить поиск, положив 
, иначе перейти к шагу 2.
Градиентный метод с постоянным шагом
Основная проблема в градиентных методах – это выбор шага ak. Достаточно малый шаг ak обеспечивает убывание функции, то есть выполнение неравенства: f(xk - akf `( xk))) < f(xk),
 |
но может привести к неприемлемо большому количеству итераций, необходимых для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции (невыполнение условия убывания) либо привести к колебаниям около точки минимума. Однако проверка усл–я убывания на каждой итерации является довольно трудоемкой, поэтому в методе град–го спуска с постоянным шагом задают a=ak пост–м и дост–но малым, чтобы можно было использовать этот шаг на любой итерации. При этом приходится мириться с возможно большим кол–вом итераций. Утешением является лишь то, что трудоемкость каждой итерации, в этом случае, минимальна (нужно вычислять только градиент f`(xk).
Схема алгоритма
Шаг 1. Задаются начальное приближение х0, постоянный шаг a, условия останова алгоритма e3. Вычисляется значение градиента f`(xk) – направление поиска. Присваивается к=0.
Шаг 2. Определяется точка очередного эксперимента:
хк+1 = хк - af’(xk),
или, в координатной форме:
 |
Шаг 3. Вычисляется значение градиента в точке хк+1:
,
или, в координатной форме:
Шаг 4. Если || f ` (xk+1) ||£e3, то поиск заканчивается, при этом:
Иначе к=к+1 и переходим к шагу 2.
Градиентный метод с дроблением шага
В методе градиентного спуска с дроблением шага величина шага aк выбирается так, чтобы было выполнено неравенство:
f(xk-ak 
)-f(xk)£-dak|| f ` (xk) ||2, где 0<d<1 – произвольно выбранная постоянная (одна и та же для всех итераций). Это требование на выбор шага aк более жесткое, чем условие убывания, но имеет тот же смысл: функция должна убывать от итерации к итерации. Однако при выполнении неравенства функция будет уменьшаться на гарантированную величину, определяемую правой частью неравенства.
 |
Процесс выбора шага протекает следующим образом. Выбираем число a>0, одно и то же для всех итераций. На к-й итерации проверяем вып–е нер–ва при aк=a. Если оно выполнено, полагаем aк=a и переходим к след–ей итерации. Если нет, то шаг aк дробим, напр–р уменьшаем каждый раз в два раза, до тех пор, пока оно не выполнится.
Схема алгоритма
Шаг 1. Задаются х0, e3, d и начальное значение шага a. Вычисляется значение градиента f`(x 0) – направление поиска. Присваивается к=0.
Шаг 2. Проверяется условие: f(xk-a )£-da|| ||2. Если выполняется, то переходим к шагу 3, иначе дробим значение a (a=a/2) и повторяем шаг 2.
Шаг 3. Определяется точка очередного эксперимента: хк+1 = хк - a f`(xk).
Шаг 4. Вычисляется значение градиента в точке хк+1: f `(хк+1).
Шаг 5. Если || f`(xk+1) ||£e3, то поиск заканчивается, при этом:
Иначе к=к+1 и переходим к шагу 2.
Метод наискорейшего спуска
В градиентном методе с постоянным шагом величина шага, обеспечивающая убывание функции f(x) от итерации к итерации, оказывается очень малой, что приводит к необходимости проводить большое количество итерации для достижения точки минимума. Поэтому методы спуска с переменным шагом являются более экономными. Алгоритм, на каждой итерации которого шаг aк выбирается из условия минимума функции f(x) в направлении движения, то есть:
называется методом наискорейшего спуска. Разумеется, этот способ выбора aк сложнее ранее рассмотренных вариантов.
Реализация метода наискорейшего спуска предполагает решение на каждой итерации довольно трудоемкой вспомогательной задачи одномерной минимизации. Как правило, метод наискорейшего спуска, тем не менее, дает выигрыш в числе машинных операций, поскольку обеспечивает движение с самым выгодным шагом, ибо решение задачи одномерной минимизации связано с дополн–ми вычислениями только самой функции f(x), тогда как основное машинное время тратится на вычисление ее градиента f ` (xk).
Следует иметь в виду, что одномерную минимизацию можно производить любым методом одномерной опт–ции, что порождает разл–е варианты метода наискорейшего спуска.
Схема алгоритма
Шаг 1. Задаются х0, e3. Вычисляется градиент f `(x0), направление поиска.
Присваивается к=0.
Шаг 2.Опр–тся точка очередного эксперимента:
хк+1 = хк - a к f``(xk), где aк – минимум задачи одномерной минимизации:
 |
Шаг 3.Вычисляется значение градиента в точке хк+1: f`(xk+1)..
Шаг 4. Если || ||£e3, то поиск точки минимума заканчивается и полагается:
 |
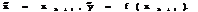Иначе к=к+1 и переход к шагу 2.
Метод покоординатного спуска
Желание уменьшить объем вычислительной работы, требуемой для осуществления одной итерации метода наискорейшего спуска, привело к созданию методов покоординатного спуска.
Пусть - нач–ое приближение. Вычислим частную производную по первой координате и примем:
где е1={1,0,…,0}T – единичный вектор оси х(1). Следующая итерация состоит в вычислении точки х2 по формуле:
где е2={0,1,0,…,0}T – единичный вектор оси х(2) и т. д.
Таким образом, в методах координатного спуска мы спускаемся по ломанной, состоящей из отрезков прямых, параллельных координатным осям.
Спуск по всем координатам составляет одну «внешнюю» итерацию. Пусть к – номер очередной внешней итерации, а j – номер той координаты, по которой производится спуск. Тогда формула, определяющая следующее приближение к точке минимума, имеет вид:
 |
где к=0,1,2,… ; j=1,2,…n.
В координатной форме формула выглядит так:
После j=n счетчик числа внешних итераций к увеличивается на единицу, а j принимает значение равное единице.
Величина шага aк выбирается на каждой итерации аналогично тому, как это делается в градиентных методах. Например, если aк=a постоянно, то имеем покоординатный спуск с постоянным шагом.
Схема алгоритма покоординатного спуска с постоянным шагом
Шаг 1. При к=0 вводятся исходные данные х0, e1, a.
Шаг 2. Осуществляется циклический по j (j=1,2,…,n) покоординатный спуск из точки хkn по формуле:
Шаг 3. Если ||x(k+1)n – xkn||£e1, то поиск минимума заканчивается, причем:
Иначе к=к+1 и переходим к шагу 2.
 |
Если же шаг aк выбирается из условия минимума функции:
 |
 |
то мы получаем аналог метода наискорейшего спуска, называемый обычно методом Гаусса – Зейделя.
Схема метода Гаусса – Зейделя
Шаг 1. При к=0 вводятся исходные данные х0, e1.
Шаг 2. Осуществляется циклический по j (j=1,2,…,n) покоординатный спуск из точки хkn по формулам:
 |
где akn+j-1 является решением задачи одномерной минимизации функции:
Шаг 3. Если ||x(k+1)n – xkn||£e1, то поиск минимума заканчивается, причем:
 |
Иначе к=к+1 и переходим к шагу 2.
Эвристические алгоритмы
Иногда, используя градиентный спуск для минимизации функций со сложной топографической структурой, применяют эвристические схемы, которые идейно близки к методам спуска. Мы рассмотрим две такие схемы.
Первая эвристическая схема содержит два основных этапа. Оба этапа представляют собой аналоги градиентного спуска с постоянным шагом. Только вместо градиента f ` (xk) используется вектор g(x), формируемый из координат f ` (xk), но на каждом из этапов по разным правилам.
На первом этапе задается малое число d1<<1 и используется градиентный спуск, где вместо градиента f ` (xk) берется вектор (x)={g(1)(x),…,g(n)(x)}, который определяется следующим образом:
 |
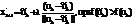Таким образом, спуск производится лишь по тем переменным, в направлении которых производная целевой функции достаточно велика. Это позволяет быстро спуститься на «дно оврага». Мы спускаемся до тех пор, пока метод не зациклится, то есть до тех пор, пока каждая следующая итерация позволяет найти точку, в которой значение функции меньше, чем значение, найденное в предыдущей итерации. После этого переходим к следующему этапу.
На втором этапе задается некоторое большое число d2>>1 и используется процедура спуска, где вместо градиента f ` (xk) берется вектор g(x)={g(1)(x),…,g(n)(x)}, который определяется следующим образом:
В этом случае перемещение происходит по «берегу» оврага вдоль его «дна». Как и на первом этапе, спуск продолжается до тех пор, пока метод не зациклится.
После выполнения первого и второго этапов принимается решение о завершении работы или продолжении. Для этого сравнивается норма разности предыдущей точки, то есть точки, которую мы имели до применения первого и второго этапов, с текущей точкой, то есть полученной после применения с точностью решения задачи e1. Если эта норма меньше e1 и норма градиента в текущей точке меньше e3, то поиск заканчивается и последняя вычисленная точка принимается за приближенное решение задачи. Иначе для текущей точки вновь повторяем первый и второй этапы и т. д.
Схема алгоритма
Шаг 1. Задаются х0, e1, e3,d1,d2,a1 – постоянный шаг пункта 1 и a2 – постоянный
шаг пункта 2 (a1<a2). Присваивается к=0.
Шаг 2. (Первый этап).
Из точки хк осуществляется спуск на «дно оврага» с постоянным шагом
a1. При спуске вычисление очередной точки осуществляется с
использованием формул:
xj+1 = xj - a1g(xj), где g(x)={g(1)(x),…,g(n)(x)},
 |
Пусть этот процесс остановится в точке xl.
Шаг 3. (Второй этап).
Из точки xl осуществляется спуск вдоль «дна оврага» с постоянным шагом a2. При спуске используются формулы: xj+1 = xj - a2g(xj), где
g(x)={g(1)(x),…,g(n)(x)},
Пусть этот процесс остановился в точке xm.
Шаг 4.
Если ||xk – xm|| £ e1 и || f ` (xm) || £ e3, то полагаем:
и поиск минимума заканчивается.
Иначе k=m и переходим к шагу 2.
Дата добавления: 2018-08-06; просмотров: 2022; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!