Перетворення зсуву, масштабування, перетворення повороту
Геометричні перетворення (перенос, масштабування, обертання)
Геометричні об'єкти на площині й у просторі можна піддавати ряду різних перетворень. Найбільш уживаними в завданнях комп'ютерної графіки є:
- переміщення (паралельний перенос);
- зміна розмірів (масштабування);
- повороти навколо деякої крапки на площині або деякій осі в просторі (обертання).
Надалі ми часто будемо ототожнювати крапки простору з радіус-вектором, обумовленим цією крапкою.
Перетворення, які відбуваються над точкою М можна розглядати у двох варіантах: зміна координатної системи, а точка зберігається; координатна система зберігається незмінною, а змінюється точка, її положення та координати.
Перетворення, під час якого точці М ставиться у відповідність точка М’, при чому точка М належить одній системі координат, а точка М’ – новій (перетвореній) системі координат, але має в ній такі самі координати називається афінним перетворенням.
До основних перетворень відносяться:
1. Зсув на вектор. Паралельний перенос об'єкта зводиться до переміщення всіх його крапок на те саме відстань 
у тому самому напрямку, заданому певним вектором 
. Якщо цей вектор має довжину 
, то операція переносу може бути реалізована шляхом додавання всіх крапок об'єкта з вектором .
2. Масштабування. Масштабування об'єкта можна реалізувати шляхом множення координат всіх його крапок на деяке число.
|
|
|
 |
3. Поворот на кут. Обертання в площині переміщають крапки по дузі окружності, центр якої перебуває на початку координат. У випадку тривимірного простору міркування, що стосуються переносу й масштабування, повністю аналогічні, тільки вони поширюються на третю координату крапок.
 |
Задача: даний трикутник АВС, координати вершин А(1,1), В(2,3), С(3,1). Виконати такі перетворення: 1. Поворот на кут π/2; 2. Розтягнення з коефіцієнтом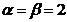 
; 3. Зсув на вектор (3,5).
3.
Відтинання, проективне перетворення,
Растрове перетворення відсікання відрізків
Методи відтинання: в основі пошуку цілочислового оптимуму лежить ідея поступового звуження області допустимих розв’язків. Спочатку задачу розв’язують без урахування вимог цілочисловості змінних, тобто використовують послаблені обмеження, а потім цілочисловість змінних враховують, ввівши додаткові обмеження. Геометрично введення додаткового лінійного обмеження означає проведення прямої, яка відтинає від багатогранника допустимих розв’язків ту його частину, яка містить точки з нецілочисловими координатами, але не торкається цілочислових точок даної множини. Багатогранник зменшують доти, доки змінні оптимального розв’язку не набудуть цілочислових значень.Якщо зображення виходить за межі екрану, то на частини дисплеїв збільшується час побудови за рахунок того, що зображення будується в "думці". У деяких дисплеях вихід за межі екрану приводить до спотворення картини, оскільки координати просто обмежуються при досягненні ними граничних значень, а не виконується точний розрахунок координат перетину (ефект "стягання" зображення). Деякі, в основному, прості дисплеї просто не допускають виходу за межі екрану. Все це, особливо у зв'язку з широким використанням технології перегляду вікнами, вимагає виконання відсікання сцени по межах вікна видимості.
|
|
|
У простих графічних системах достатньо двовимірного відсікання, в тривимірних пакетах використовується три і чотиривимірне відсікання. Останнє виконується в раніше розглянутих однорідних координатах, що дозволяють єдиним чином виконувати аффінні і перспективні перетворення.
Програмного виконання відсікання достатньо повільний процес, тому, природно, в могутні дисплеї вбудовується відповідна апаратура.
Відрізки, що відсікаються, можуть бути трьох класів - цілком видимі, цілком невидимі і такі, що перетинають вікно. Очевидно, що доцільно можливо раніше, без виконання великого об'єму обчислень ухвалити рішення про видимість цілком або відкиданні. За способом вибору простого рішення про відкидання невидимого відрізка цілком або ухвалення його існує два основні типи алгоритмів відсікання - алгоритми, що використовують кодування кінців відрізка або всього відрізка і алгоритми, що використовують параметричне представлення відрізків, що відсікаються, і вікна відсікання. Представники першого типу алгоритмів - алгоритм Коена-сазерленда (Cohen-Sutherland, CS-алгоритм) і FC-алгоритм (Fast Clipping - алгоритм). Представники алгоритмів другого типу - алгоритм Кируса-Бека (Curus-Beck, CB - алгоритм) і пізніший алгоритм Ліанга-Барські (Liang-Barsky, LB-алгоритм).
|
|
|
Алгоритми з кодуванням застосовуються для прямокутного вікна, сторони якого паралельні осям координат, тоді як алгоритми з параметричним уявленням застосовані для довільного вікна.
Дата добавления: 2018-06-27; просмотров: 771; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!