Правило Рунге практической оценки погрешности

Как следует из последней теоремы, главный член погрешности квадратурной формулы интерполяционного типа имеет вид

Непосредственное использование этой формулы для оценки погрешности I - I^h неудобно, т.к. требует вычисления производных функции f. В более сложных ситуациях выражение для главного члена погрешности может оказаться существенно более громоздким. Поэтому в вычислительной практике часто применяются методы оценки погрешности, не использующие явное выражение для главного члена. Вычитая из равенства (28) равенство (29), получаем

Учитывая приближенное равенство (29), приходим к следующей приближенной формуле:

(30)

Использование этой формулы для оценки погрешности I^h^/2 принято называть правилом Рунге (или правилом двойного пересчета).

Замечание 1. Т.к. , то из (30) следует формула , которую можно было бы использовать для приближенной оценки погрешности значения I^h. Как правило, этого не делают, поскольку среди двух вычисляемых значений интеграла I^h и I^h^/2 второе является более точным и имеет смысл оценивать именно его погрешность.

Замечание 2. Заменой h на 2h формула (30) приводится к следующему виду

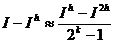(31)

Для формул прямоугольников и трапеций R=2 (см.(25) и (26)), для формулы Симпсона R=4 (27), поэтому для этих квадратурных формул равенство (31) принимает вид:

(32)

(33)

(34)

Кроме правила Рунге существуют и другие способы оценки погрешности. Например, можно использовать значение , вычисленные по формулам прямоугольников и трапеций с одним и тем же шагом, для практической оценки погрешности каждого из этих значений. Действительно, в равенствах (25), (26) C_mp = -2 C_np, поэтому

откуда следует, что

(35)

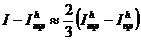(36)

Наличие некоторого правила получения оценки погрешности позволяет строить процедуры вычисления интеграла I с заданной точностью ε, достигаемой последовательным дроблением шага интегрирования. Простейшая процедура такого типа состоит в последовательном вычислении значений и соответствующих оценок погрешности ε_i (например, по правилу Рунге) для h_i = h_o / 2_i, где h_o – начальное значение шага, i = 1, 2, … Вычисления прекращаются тогда, когда при некотором i оказывается | ε_i | < ε (требуемая точность достигнута), либо тогда, когда величина | ε_i | начинает возрастать (точность не может быть достигнута из-за влияния вычислительной погрешности).

Адаптивные процедуры численного интегрирования

До сих пор мы рассматривали методы численного интегрирования с постоянным шагом. Однако они обладают значительно меньшей эффективностью и используются в вычислительной практике существенно реже, чем методы с переменным шагом. Объясняется это тем, что равномерно распределяя узлы по отрезку интегрирования, мы полностью игнорируем особенности поведения подынтегральной функции, хотя интуитивно ясно, что на участках плавного изменения функции достаточно поместить сравнительно небольшое число узлов, разместив значительно большее их число на участках резкого изменения функции. Распределение узлов интегрирования в соответствии с характером поведения подынтегральной функции часто позволяет при том же общем числе узлов получить значительно более высокую точность. Тем не менее выбор соответствующего неравномерного распределения узлов интегрирования является очень сложной задачей , и вряд ли мог быть широко использован на практике, если бы для решения этой задачи не удалось привлечь компьютер.

Современные процедуры численного интегрирования (адаптивные квадратурные программы) используют некоторый алгоритм автоматического распределения узлов интегрирования. Пользователь такой программы задает отрезок [a, b], правило вычисления функции f и требуемую точность ε > 0. Программа стремиться, используя по возможности минимальное число узлов интегрирования, распределять их так, чтобы найденное значение удовлетворяло неравенству

(37)

Здесь - приближенное значение интеграла , вычисленное по некоторой формуле.

Типичная программа разбивает исходный отрезок [a, b] на элементарные отрезки [x_i_-1, x_i] так, чтобы для погрешностей выполнялось неравенство:

При этом каждый из элементарных отрезков получается, как правило, делением пополам одного из отрезков, найденного на более раннем шаге алгоритма. Заметим, что последнее неравенство выполняется, если каждая из погрешностей удовлетворяет условию |R_i| < h_i ε/(b - a).

Действительно, тогда

Рассмотрим одну из простейших адаптивных процедур, основанную на формуле трапеций:

(38)

и использующую для контроля точности составную формулу трапеций с шагом h_i / 2:

(39)

Если значение уже найдено, то для нахождения значения требуется лишь одно дополнительное вычисление функции f в точке x_i_-1/2.

Можно показать, что для оценки погрешностей квадратурных формул интерполяционного типа на элементарных отрезках правили Рунге сохраняет силу, поэтому погрешность приближенного значения можно оценить по формуле

(40)

В рассматриваемой адаптивной процедуре последовательно выбирают точки x_i и вычисляют значения

(i = 1, 2, …, n),

последнее из которых S_n совпадает с I^h и принимается за приближенное значение интеграла I. Перед началом работы полагают S₀=0, x₀=a и задают некоторое начальное значение шага h₁.

Опишем i – тый шаг процедуры в предположении, что значение S_i_-1 уже найдено, и очередное значение шага h_i определено.

1. По формулам (38) – (40) – вычисляют значения , , ε_i.

2. Если | ε_i | >h_i ε /(b - a), то шаг h_i уменьшают в 2 раза, и повторяются вычисления п.1.

3. После того, очередное дробление шага приводит к выполнению условия | ε_i | ≤ h_i ε /(b - a), вычисляют значения x_i = x_i_-1+ h_i, S_i = S_i_-1+ .

4. Если x_i + h_i > b, то полагают h_i₊₁ = b - x_i.

В противном случае h_i₊₁ = h_i.

На этом i - тый шаг завершается.

Замечание 1. В некоторых адаптивных процедурах при выполнении условия типа | ε_i | << h_i ε /(b - a) очередное значение шага удваивается h_i₊₁ =2h_i. Таким образом, шаг интегрирования в зависимости от характера поведения подынтегральной функции может не только измельчаться, но и укрупняться.

Замечание 2. Известно, что при оптимальном распределении узлов интегрирования модули погрешностей, приходящихся на элементарные отрезки интегрирования, должны быть примерно одинаковыми. Распределение узлов, полученное с помощью адаптивных процедур, как правило, не является таковым. Однако для большинства функций оно является в полнее удовлетворительным.

Итак, мы в основном рассматривали не вычислительные алгоритмы, а методы дискретизации, то есть методы замены определенных интегралов соответствующими квадратурными суммами. Как бы ни был организован алгоритм, он все же предполагает вычисление квадратурной суммы. С увеличением числа слагаемых возрастает влияние вычисляемой погрешности на результат суммирования. При очень больших значениях N доже для хорошо обусловленных квадратурных формул соответствующий алгоритм может стать плохо обусловленным.

Кроме того, при вычислении кратных интегралов уже при не очень больших значениях m ≥ 6 применение кубатурных формул такого большого числа N вычислений значений функции f, что решение задачи даже при использовании самых современных компьютеров становиться нереальным.

Кратный интеграл вычисляется для функции многих переменных по замкнутой ограниченной многомерной области. Вычислительная схема имеет вид: интервал, соответствующий изменению каждой переменной внутри области интегрирования, разбивается на фиксированное число отрезков. Таким образом, задается разбиение области интегрирования на определенное число элементарных многомерных объемов. Вычисляются значения подынтегральной функции для точек, взятых по одной внутри каждого элементарного объема, и полученные значения суммируются. При увеличении кратности интеграла число слагаемых очень быстро возрастает.

В таких ситуациях для получения значения интеграла предпочтительнее использовать метод Монте – Карло, при котором погрешность (в отличие от рассмотренных нами методов численного интегрирования) оценивается не гарантированно, а лишь с некоторой степенью достоверности.

Метод Монте – Карло

Метод Монте – Карло состоит в том, что задается случайная величина ξ, математическое ожидание которой равно искомой величине z, то есть

M(ξ) = z (41)

Осуществляется серия n независимых испытаний случайной величины ξ: ξ₁, ξ₂, …, ξ_n и приближенно полагается

(42)

В силу (41) при любом натуральном n

(43)

Если дисперсия D(ξ) = σ² конечна, то

, (44)

причем в силу центральной предельной теоремы распределение случайной величины асимптотически нормально.

Поэтому при достаточно большом n (практически при n > 10) согласно (43), (44) и известному правилу «трех сигм», имеем

, то есть неравенство (45)

выполняется с вероятностью, достаточно близкой к единице (» 0,997).

На практике, если σ неизвестна, но во всяком случае конечна, то ее оценивают при n > 10 по формуле

(46)

12.1. Вычисление определенных интегралов.

Рассмотрим интеграл

, (47)

Который может быть и несобственным интегралом, но таким, что интеграл тоже существует

h - равномерно распределенная на отрезке [0, 1] случайная величина, то есть имеющая плотность распределения

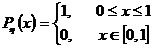
Тогда ξ = f(h) тоже будет некоторой случайной величиной, причем по определению математического ожидания

Таким образом, (48)

Где h_i – независимые реализации случайной величины h. Поскольку наряду с (7) по предположению существует то

(49)

Величину h оценивают либо по формуле (46), либо исходя из (49), оценивая сверху, а снизу например, нулем. Погрешность оценивается по формуле (45) с вероятностью » 0,997.

Кратные интегралы методом Монте – Карло вычисляются аналогично. Например,

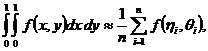(50)

Где h_i, q_i – независимые реализации равномерно распределенных на [0, 1] случайных величин h, q.

Случайные величины (случайные числа), равномерно распределенные на отрезке [0, 1], в современных ЭВМ задаются с помощью специальных физических датчиков или программ. При применении программ, эти числа называются псевдослучайными, хотя практически они обладают статистическими характеристиками, свойственными случайными величинами, но строго говоря, они не являются случайными.

Дата добавления: 2018-06-27; просмотров: 648; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!