Квадратурные формулы интерполяционного типа.

Численное интегрирование

1. Постановка задачи. В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла.

(1)

Этот интеграл может выражать площадь, объем, работу переменной силы и т.д.

Если функция f(x) непрерывна на отрезке [a, b], и её первообразную F(x) удается выразить через известные функции, то для вычисления интеграла (1) можно воспользоваться формулой Ньютона – Лейбница

(2)

/* Готфрид Вильгельм Лейбниц (1646-1716) – немецкий математик, физик и философ. Один из создателей дифференциального и интегрального исчислений*/

К сожалению, в подавляющем большинстве случаев получить значение определенного интеграла с помощью формулы (2) или других аналитических методов не удается. И даже тогда, когда удается получить первообразную функцию F(x) в аналитической форме, значительные усилия, затраченные на это, часто оказывается чрезмерно высокой платой за окончательный результат, поскольку вычисления интеграла в этих случаях по формуле (2) приводят к громоздким, а часто и приближенным вычислениям. Часто найти точное значение интеграла просто невозможно, например, когда функция f(x) задана таблицей своих значений.

Обычно для вычисления значения определенного интеграла применяют специальные численные методы. Наиболее широко используются на практике квадратурные формулы – приближенные равенства вида

(3)

где – некоторые точки [a, b] - узлы квадратурной формулы

A_i – числовые коэффициенты, называемые весами квадратурной формулы

N ≥ 0 – целое число.

Сумма , которая принимается за приближенное значение интеграла, называемое квадратурной суммой.

Величина называется погрешностью (или остаточным членом) квадратурной формулы.

В многомерном случае (когда размерность интеграла больше единицы) формулы для приближенного вычисления интеграла называют кубатурными.

Будем говорить, что квадратурная формула (3) точна для многочленов степени m, если для любого многочлена степени не выше m эта формула дает точное значение интеграла, т.е.

При оценке эффективности квадратурных формул часто исходят из того, что наиболее трудоемкой операцией при выполнении по формуле (3) является нахождение функции f. Поэтому среди двух формул, позволяющих вычислить интеграл с заданной точностью ε, более эффективной считается то, в которой используется меньшее число узлов.

Выведем простейшие квадратурные формулы, использовав наглядные геометрические соображения. Будем интерпретировать интеграл (1) как площадь криволинейной трапеции, ограниченной графиком функции f(x) (при f(x) ≥ 0), осью абсцисс и прямыми x = a, x = b (рис. 1а).

Разобьем отрезок [a, b] на элементарные отрезки [x_i_-1, x_i] точками a = x_o < x₁< … < x_n = b. Интеграл I разобьется при этом на сумму элементарных интегралов

, (4)

Где , что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис. 1б)

Введем обозначения fi=f(xi) f_i_-½=(x_i_-½),

где x_i_-½= - середина элементарного отрезка. Для простоты шаг h=x_i – x_i_-1 будем считать постоянным.

2. Формула прямоугольников. Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоугольника, основанием которого является отрезок [x_i_-1, x_i], а высота равна значению f_i_-½

На рис. 2а N_i_-½ обозначена точка с координатами (x_i_-½, f_i_-½). Так мы приходим к элементарной квадратурной формуле прямоугольников: I_i » hf_i_-½ (5)

Производя такую замену для всех элементарных криволинейных трапеций, получаем составную квадратурную формулу прямоугольников

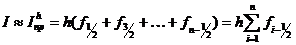(6)

Эта формула соответствует приближенной замене площади исходной криволинейной трапеции площадью ступенчатой фигуры, изображенной на рис. 2б.

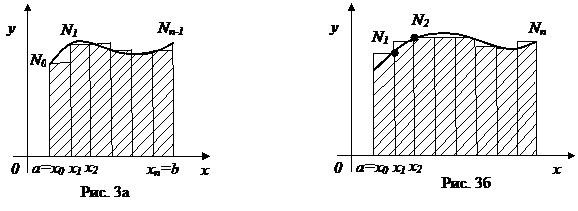
Замечание. Иногда используют формулы

(7)

(8)

называемые соответственно составными квадратурными формулами левых и правых прямоугольников. Геометрические иллюстрации приведены на рис. 3а, 3б. В соответствии с этим формулу (6) иногда называют составной квадратурной формулой центральных прямоугольников.

3. Формула трапеций. Соединив отрезком точки N_i_-1 (x_i_-1, f_i_-1) и N_i (x_i, f_i) на графике функции y=f(x), получим трапецию (рис. 4а). Заменим приближенно площадь элементарной криволинейной трапеции площадью построенной фигуры. Тогда получим элементарную квадратурную формулу трапеций

(9)

Пользуясь этой формулой при i=1, …, n, выводим составную квадратурную формулу трапеций:

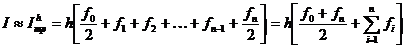(10)

Эта формула соответствует приближенной замене площади исходной криволинейной трапеции площадью фигуры, ограниченной ломаной линией, проходящей через точки N₀, N₁, …, N_n (рис. 4б).

4. Формула Симпсона. Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки N_i_-1, N_i_-½ и N_i (рис. 5а), то получим приближенное равенство

, где

P₂(x) – интерполяционный многочлен второй степени с узлами x_i_-1, x_i_-½, x_i

Поскольку P₂(x_i_-1)=f_i_-1, P₂(x_i_-½)=f_i_-½, P₂(x_i)=f_i, верна формула

Ее интегрирование приводит к равенству

Таким образом, выведена элементарная квадратурная формула Симпсона:

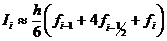(11)

/* Формула Симпсона впервые была получена Кавальери в 1639г., затем в 1668г. она была переоткрыта Джеймсом Грегори. Томас Симпсон, английский математик (1710-1761), вывел ее в 1743 году*/

Применяя эту формулу на каждом элементарном отрезке, выводим составную квадратурную формулу Симпсона:

(12)

Замечание 1. Учитывая геометрическую интерпретацию формулы Симпсона, ее иногда называют формулой парабол.

Замечание 2. Когда число элементарных отрезков разбиения четно n=2_m, в формуле Симпсона можно использовать узлы с целыми индексами

При выводе этой формулы роль элементарного отрезка играет отрезок [x₂_i_-2, x₂_i] длины 2h.

5. Оценка погрешности. Оценим погрешность выведенных квадратурных формул в предположении, что подынтегральная функция f достаточно гладкая.

Будем использовать обозначение Mk = max (f⁽^k⁾(x)) [a, b]

Теорема. Пусть функция f дважды непрерывно дифференцируема на отрезке [a, b]. Тогда для составных квадратурных формул прямоугольников и трапеций справедливы следующие оценки погрешности:

(13)

(14)

Доказательство: Для вывода оценки (13) представим погрешность формулы прямоугольников в виде

Используя формулу Тейлора

где x Є [xi-1, xi], ζ = ζ (x) Є [xi-1, xi], имеем

Т.к. то

Замечая, что nh = b - a, приходим к оценке (13).

Для вывода оценки (14) воспользуемся тем, что отрезок, соединяющий точки N_i_-1 и N_i представляет собой график интерполяционного многочлена первой степени

Поэтому для элементарной формулы трапеций верно равенство:

Используя оценку погрешности линейной интерполяции

имеем

Следовательно, для справедлива оценка

Приведем без доказательства теорему об оценке погрешности формулы Симпсона:

Пусть функция f имеет на отрезке [a, b] непрерывную производную четвертого порядка f⁽⁴⁾. Тогда для формулы Симпсона (12) справедлива оценка погрешности

(15)

Замечание 1. Оценки (13) – (15) означают, что формулы прямоугольников и трапеций имеют второй порядок точности относительно h, а формула Симпсона – четвертый порядок точности. Из тех же оценок следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона – для многочленов третьей степени.

Замечание 2. Формулы (7) и (8) имеют лишь первый порядок точности (абсолютная погрешность каждой из формул не превышает 0,5 M₁(b - a) h) и поэтому для вычисления интегралов на практике они используются крайне редко.

6. Случай переменного шага. Приведем составные квадратурные формулы прямоугольников, трапеций и Симпсона с переменным шагом h_i = x_i - x_i_-1

Вывод этих формул и их геометрический смысл остаются теми же, что и для постоянного шага. Теоремы об оценках погрешности также останутся справедливыми, если в неравенствах (13) - (15) заменить h на

Квадратурные формулы интерполяционного типа.

Для приближенного вычисления определенного интеграла часто используется естественный для методов приближения функций прием. Подынтегральную функцию f аппроксимируют на отрезке [a, b] некоторой функцией g, интеграл от которой легко вычисляется, затем полагают

(16)

Точность формулы (16) можно повышать за счет усложнения метода глобальной аппроксимации. Однако чаще используют другой подход. Интеграл I представляется в виде суммы (4) интегралов по элементарным отрезкам [x_i_-1, x_i]. На каждом таком i-м отрезке функцию f аппроксимируют некоторой легко интегрируемой функцией g_i. В результате получается составная формула

Рассмотрим этот подход более подробно в случае, когда аппроксимация осуществляется с помощью интерполяционного многочлена.

Зафиксируем некоторые узлы t₀, t₁, …, t_m Є [-1, 1]. Аппроксимируем функцию f(x) на некотором элементарном отрезке [x_i_-1, x_i] интерполяционным многочленом Pm,i (x) с узлами интерполяции

В случае, когда все значения t_j различны, можно воспользоваться записью интерполяционного многочлена в форме Лагранжа:

(17)

Использовав замену переменной вычислим интеграл от Pm,i на отрезке [x_i_-1, x_i]:

Приближенная замена интеграла I суммой

приводит к следующей составной квадратурной формуле интерполяционного типа

(18)

Замечание. Квадратурные формулы интерполяционного типа, постоянные на основе равноотстоящих значений t₀, t₁, …, t_m называют формулами Ньютона – Котеса.

/* Роджер Котес (1682-1716) – английский математик, друг и ученик И.Ньютона*/

Приведем квадратурные формулы Ньютона-Котеса, отвечающие использованию многочленов степени m = 1, 2, 3, 4, 5, 6 соответственно.

m=1 – формула трапеций;

m=2 – формула Симпсона;

m=3 правило ⅜;

m=4 формула Милна (формула Боде);

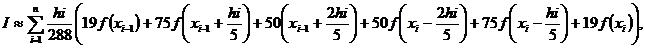m=5; m=6 – формула Вэддла;

Оценка погрешности.

Приведем теорему об оценке погрешности формулы (18).

Пусть функция f имеет на отрезке [a,b] непрерывную производную порядка m+1. Тогда для погрешности квадратурной формулы (18) справедливая оценка

(19)

где

Доказательство: представим погрешность R=I-I^h формулы (18) в виде

Пользуясь оценкой погрешности интерполяции, в данном случае принимающей вид

и производя замену переменной x=x_i_-½+thi/2, получаем цепочку неравенств:

Учитывая, что приходим к оценке (19).

Замечание 1. Теорема остается справедливой и в случае, когда для построения квадратурной формулы используется интеграция с кратными узлами (т.е. когда некоторые из значений (t₀, t₁, …, t_m)совпадают.)

Замечание 2. Как следует из оценки (19), квадратурные формулы интерполяционного типа (18) точны для многочленов степени m.

Приведем оценки погрешности формул Ньютона – Котеса.

m=1 – формула трапеций

m=2 – формула Симпсона

m=3 – правило ⅜

m=4 – формула Милна (формула Боде)

m=5

m=6 – формула Вэддла

Квадратурные формулы Гаусса

Мы рассмотрели, что квадратурная формула

построенная интегрированием интерполяционного многочлена степени N с фиксированными узлами x₀, x₁, …, x_N , точна для всех многочленов степени N. Однако, если имеется свобода в выборе узлов, то можно распорядиться ею так, чтобы получить формулу, точную для всех многочленов некоторой степени, превышающей N.

Поставим следующую задачу: при заданном числе N+1 узлов построить квадратурную формулу, точную для многочленов наиболее высокой степени. Формулы, удовлетворяющие этому условию, принято называть квадратурными формулами Гаусса. Как правило, сначала строят формулы Гаусса.

(20)

для стандартного отрезка [-1, 1]. Затем с помощью замены переменной

осуществляют переход к формулам интегрирования на произвольном отрезке:

(21)

Заметим, что формула (20) точна для многочленов степени тогда и только тогда, когда она точна для функций f(x)=1, t, t², …, t^m.

Это эквивалентно тому, что узлы ti и веса ai формулы (20) д. удовлетворять системе нелинейных уравнений

(22)

Можно показать, что система (22) имеет единственное решение a₀, a₁, …, a_N, t₀, t₁, …, t_N (причем, ti Є [-1, 1]) тогда и только тогда, когда число уравнений системы совпадает с числом неизвестных, т.е. при m=2N+1.

Пример. Построим квадратурную формулу Гаусса с двумя узлами. В этом случае, т.е. при N=1, m=3 система (22) примет вид

Решаем ее, находим значения a₀= a₁=1, t₀ = -1/√3, t₁=1/√3. Таким образом, получаем квадратурную формулу Гаусса

точную для многочленов третьей степени. Для квадратурной формулы Гаусса (20) справедлива следующая оценка погрешности:

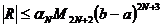
Входящий в нее коэффициент

очень быстро убывает с ростом N.

Можно было бы разбить отрезок интегрирования на частичные отрезки и, исходя из формулы Гаусса, построить составную формулу, имеющую порядок точности, равный 2N + 2. Однако при интегрировании достаточно гладких функций в этом нет необходимости, т.к. уже при небольшом числе узлов (4 ≤ N ≤ 10) формула Гаусса обеспечивает очень высокую точность. На практике используются и формулы с десятками и сотнями узлов.

Численные значения узлов и весов квадратурных формул Гаусса для значений N до 95 приведены в математических справочниках.

Замечание. Известно, что узлы квадратурных формул Гаусса G_N совпадают с корнями многочленов Лежандра P_N(x), поэтому эти квадратурные формулы иногда называют формулами Гаусса – Лежандра.

Понятие об адаптивных процедурах численного интегрирования

Применение неравенств типа (13) - (15), (19) для оценки погрешности квадратурных формул в большинстве случаев оказывается неэффективным или вообще невозможным. Это связано как с трудностями оценивания производных подынтегральной функции f, так и с тем, что получаемые оценки, как правило, бывают сильно завышенными.

На практике обычно используются иные походы к оценке погрешности, позволяющие строить процедуры численного интегрирования с автоматическим выбором шага.

10.1 Главный член погрешности.

Пусть I^h – приближенное значение интеграла 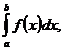вычисленное по некоторой квадратурной формуле и использующее разбиение отрезка [a, b] на элементарные отрезки длины h. Предположим, что для погрешности этой формулы справедливо представление

I - I^h= Ch^k+ 0(h^k) (23)

где c≠0 и k>0 – величины, не зависящие от h.

Тогда величина названа главным членом погрешности квадратурной формулы.

/* Запись φ(h) = 0(h^k) (читается «φ(h) есть 0 малое от h^k») означает, что φ(h)/h^k→0 при h→0*/

Из неравенства (23) следует справедливость оценки с некоторой постоянной , поэтому число k представляет собой не что иное, как порядок точности соответствующей квадратурной формулы.

Если подынтегральная функция f достаточно гладкая, то для каждой из составных квадратурных формул

(24)

существует главный член погрешности.

Приведем без доказательства соответствующий результат.

Теорема. Пусть и k – минимальное среди натуральных чисел, для которых величина отлична от нуля. Если функция f непрерывно дифференцируемая R раз на отрезке [a, b], то для погрешности квадратурной формулы (24) справедливо представление (23), в котором

Следствие 1. Если функция f дважды непрерывно дифференцируема на [a, b], то для погрешностей составных квадратурных формул прямоугольников и трапеций справедливы следующие представления

(25)

(26)

Следствие 2. Если функция f четырежды непрерывно дифференцируема на [a, b], то для погрешности составной квадратурной формулы Симпсона справедливо представление

(27)

В силу предположения (23) для погрешности квадратурной формулы при достаточно малом h справедливо приближенное равенство

I - I^h » Ch^k (28)

Несмотря на элементарный характер формулы (28), она позволяет сделать ряд важных выводов. Например, уменьшение шага h в M раз приводит к уменьшению погрешности квадратурной формулы примерно в M^k раз. Действительно, при h₁ = h/M имеем

В частности, уменьшение шага h в 2 раза приводит к уменьшению погрешности примерно в 2^k раза

(29)

Дата добавления: 2018-06-27; просмотров: 3269; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!