На підставі центральної граничної теореми маємо
.
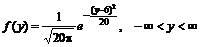Центральна гранична теорема була вперше використана для доведення інтегральної теореми Муавра—Лапласа.
Теорема Муавра—Лапласа
У загальному випадку випадкові величини Х1, Х2, … Хn, що розглядаються в центральній граничній теоремі, можуть мати довільні закони розподілу.
Якщо Хі є дискретними і мають лише два значення: P (Хі = 0) = q, P (Xі = 1) = p, то приходимо до теореми Муавра—Лапласа, яка є найпростішим випадком центральної граничної теореми.
Якщо здійснюється n незалежних експериментів, у кожному з яких імовірність появи випадкової події А є величиною сталою і дорівнює p, то для інтервалу [a; b) справедлива рівність:
(348)
| ! |
Доведення. Нехай проводиться n незалежних експериментів, у кожному з яких випадкова подія А може здійснитися зі сталою ймовірністю р. Тоді 
— поява випадкової події в n експериментах є випадковою величиною із числовими характеристиками:
M (Y) = np, D (Y) = npq, 
.
На підставі центральної граничної теореми розподіл випадкової величини Y зі зростанням n наближатиметься до нормального. Тому для обчислення ймовірності події a < Y < b використовується формула (261): 
що і треба було довести.
Приклад 9. Завод виготовляє 80% виробів першого сорту. Навмання вибирають 800 виробів. Яка ймовірність того, що число виробів першого сорту виявиться в межах від 600 до 680 штук?
Розв’язання. Із умови задачі маємо p = 0,8; q = 0,2; n = 800; a = 700, b= 620.
|
|
|
Oбчислимо: np = 800 × 0,8 = 640; 
Згідно з (259) дістанемо:
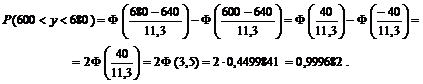
| Теоретичні запитання до теми | ? |
1. Як сформулювати в загальному вигляді закон великих чисел?
2. Сформулювати нерівність Чебишoва.
3. Довести, що 
4. Сформулювати умови, які мають виконуватися для нерівності Чебишoва.
5. Де використовується нерівність Чебишoва?
6. Сформулювати теорему Чебишoва.
7. Які умови мають виконуватися для доведення теореми Чебишoва?
8. Записати нерівність Чебишoва для теореми Чебишoва.
9. 
Довести, що 
.
10. Сформулювати теорему Бернуллі.
11. Записати нерівність Чебишoва для теореми Бернуллі.
12. Довести, що 
.
13. Дати визначення характеристичної функції для випадкової величини.
14. Чому дорівнює ax(0) ?
15. Чому дорівнює a¢x(0) ?
16. Чому дорівнює a¢¢x(0) ?
17. Чому дорівнює aY(t), якщо Y = ax + b?
18. Чому дорівнює aY(t), якщо 
?
19. Сформулювати центральну граничну теорему.
20. Довести, що для нормованого нормального закону розподілу aх(t) = ... .
21. Доведення центральної граничної теореми.
22. Використання центральної граничної теореми для доведення інтегральної теореми Муавра—Лапласа.
Приклади до теми
1. Імовірність появи випадкової події в одному експерименті є величиною сталою і дорівнює 0,3. Із якою імовірністю можна стверджувати, що відносна частота цієї події при 100 експериментах буде знаходитись у межах [0,2; 0,4].
|
|
|
Відповідь. 0,98.
2. Випадкова подія А може здійснитися при одному експерименті із імовірністю р. Експеримент повторили n раз. Яка ймовірність того, що при цьому виконується нерівність
np – 2 
< m < np + 2 .
Відповідь. 0,9544.
3. Яке повинна мати значення величина e у нерівності Чебишова, щоб 
, коли відомо, що D (Х) = 4.
Відповідь. e = 20.
4. Із якою надійністю середнє арифметичне вимірів певної величини відповідає істинному виміру цієї величини, якщо було здійснено 500 вимірювань із точністю 0,1 і при цьому дисперсії випадкових величин — результатів вимірювання — не перевищують 0,3.
Відповідь. 0,94.
5. Скільки необхідно провести вимірів діаметра втулки, щоб середнє арифметичне цих вимірів відрізнялося від істинного розміру діаметра втулки не більше як 0,05 із надійністю 90%, якщо дисперсії випадкових величин (результатів вимірів) не перевищують 0,2.
Відповідь. n = 800.
6. Імовірність того, що за час t із ладу вийде один конденсатор, дорівнює 0,2. Яка ймовірність того, що за час t із 100 конденсаторів із ладу вийде:
1) не менш як 28 конденсаторів;
|
|
|
2) від 14 до 26 конденсаторів?
Відповідь. 1) 0,98; 2) 0,9.
7. При відливанні відливок, із яких потім виготовляють на верстатах деталі, одержують у середньому 20% браку. Скільки необхідно запланувати відливок, щоб із імовірністю не меншою за 0,95 була забезпечена програма випуску деталей, для виготовлення яких необхідно 50 бездефектних відливок.
Відповідь. n = 305.
8. Здійснюється вибіркове обстеження партії електроламп для визначення тривалості їх горіння. Скільки необхідно перевірити електролампочок, щоб із імовірністю не меншою за 0,9876 можна було стверджувати, що середня тривалість горіння лампочки для всіх n штук перевірених відхилялось від її середньої величини не більше ніж на 10 годин, якщо середнє квадратичне відхилення тривалості горіння лампочок дорівнює 80 годин.
Відповідь. n = 4776.
9. Випадкова величина 
— середнє арифметичне 10000 незалежних випадкових велечин, що мають один і той самий закон розподілу, і середнє квадратичне відхилення кожної із них дорівнює 2. Яке максимальне відхилення величини від його математичного сподівання можна очікувати із імовірністю 0,9544?
Відповідь. 0,04.
10. Верстат із програмним управлінням виготовляє за робочу зміну 900 виробів, із яких в середньому 1% складає брак. Знайти наближено ймовірність того, що за зміну буде виготовлено не менше 810 доброякісних виробів, якщо вони виявляються доброякісними незалежно один від одного.
|
|
|
Відповідь. 0,99865.
11. Кожна із 40 незалежних випадкових величин має гамма-розподіл із значенями параметрів a = 2, l = 10. На підставі центральної граничної теореми теорії ймовірностей записати наближено закон розподілу для випадкової величини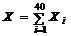 
.
Відповідь. а = 8; s » 0,9;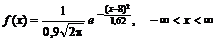 
.
12. У касі певного закладу в наявності є 4000 гривень. У черзі знаходиться n = 30 робітників. Сума X, яку потрібно виплатити кожному, є випадковою величиною із математичним сподіванням, рівним 200 грн. і середнім квадратичним відхиленням s = 60 грн. Знайти ймовірність того, що суми, котра є в касі, не вистачить усім людям, які стоять у черзі.
Відповідь. 
грн.;
грн.;
. Не вистачить.
13. Зберігається умова задачі 12, тільки в черзі стоїть n = 15 робітників і сума Х, яку повинен одержати кожний із них, є випадковою величиною із значеннями M (X) = 150 грн., s (Х) = 60 грн. Яка ймовірність того, що суми вистачить усім людям?
Відповідь. 
грн.; 
грн.;
.
Усім робітникам вистачить суми, що є в касі.
14. Залізничний состав складається із 30 вагонів. Маса кожного з них є випадковою величиною Х із математичним сподіванням M(X) = 400 т і середнім квадратичним відхиленням s(Х) = 20 т. Локомотив може нести масу не більшу за 12100 т. Якщо маса составу перевищує допустиму, то необхідно причеплювати другий локомотив. Знайти ймовірність того, що одного локомотива не досить для перевезення составу.
Відповідь. 
— маса составу.
; 
;
.
15. Маємо 100 ідентичних елементів, що складають певний технічний комплекс. Час безвідмовної роботи кожного i-го елементу є випадковою величиною Ті, що має експоненціальний закон розподілу із параметром l = 40 і однаковим для всіх елементів. Випадкові величини T1, T2, T3, ..., T100 є незалежними між собою. У разі відмови в роботі i-го елемента миттєво здійснюється переміщення на i + 1-й справний елемент. Загальний час безвідмовної роботи комплексу дорівнює сумі Ti, а саме 
. Знайти наближено ймовірність того, що комплекс безвідмовно пропрацює не менш як 20 год.
Відповідь:
.
16. Провести апроксимацію нормального закону із параметрами а, s за допомогою суми n незалежних випадкових величин Х1, Х2, ..., Хn, кожна із яких має рівномірний закон розподілу на проміжку [0; 1]
Відповідь.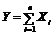 
; 
; 
; 
; 
.
17. Верстат-автомат виготовляє за робочу зміну n = 1000 виробів, із яких брак у середньому становить 5%. На скільки доброякісних виробів k має бути розрахований бункер для доброякісних виробів, щоб імовірність його переповнення за зміну не перевищувала 0,001.
Відповідь.
ЛІТЕРАТУРА
1. Вентцель Е. С., Овчаров Л. А. Теория вероятностей и ее инженерное приложение. — М.: Наука, 1988.
2. Гнеденко Б. В. Курс теории вероятностей. — М.: Наука, 1961.
Дата добавления: 2018-06-01; просмотров: 364; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!