Изучение гранулометрического состава суспензии методом оптической микроскопии
Цель работы: выявить особенности процессов образования флокул в присутствии полиэлектролитов различной природы; оценить размеры и форму частиц суспензии, а также неоднородность дисперсной системы.
Реактивы и оборудование
Реактивы: Полимер из ряда: поли-1,2-ДМ-5-ВПМС, поли-ДМАЭМА*ДМС, поли-ДМАЭМА*БХ, по заданию преподавателя, каолин марки КСД (или охра “золотистая”), дистилированная вода.
Оборудование: технические и аналитические весы, набор разновесов, узкий градуированный цилиндр на 100 см3 – 6 шт, стеклянная градуированная пипетка на 1 мл – 1 шт, химический стакан на 50 мл – 1 шт, колба мерная на 50 мл – 1 шт, магнитная мешалка с магнитным элементом, микроскоп МБС-10.
Порядок выполнения работы.
В ходе выполнения работы необходимо выполнить следующие операции:
Ø приготовить суспензию каолина (приготовление осуществляется анологично, описанному в работе 6);
Ø приготовить раствор полимера (приготовление осуществляется анологично, описанному в работе 6);
Ø исследовать гранулометрический состав суспензии.
Порядок проведения эксперимента. В цилиндр с суспензией объемом 100 см3 вводят необходимое количество раствора полимера и в течение 2-х мин с умеренной скоростью осторожно перемешивают систему дисковой мешалкой, не допуская попадания воздуха. После перемешивания из середины объема суспензии пипеткой с широким носиком аккуратно берется несколько капель и наносится на предметное стекло. Визуально при помощи микроскопа определяются размеры и форма частиц, подсчитывается их количество по фракциям (параллельно в 5-10 изолированных полях, от 20 до 40 частиц в каждом поле). Для каждой фракции рассчитывается средний радиус частиц:
|
|
|
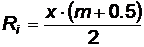, (4.11)
где x - цена деления микрометрической сетки микроскопа,
m - целое число делений для данной фракции.
Цена деления микрометрической сетки микроскопа выбирается в зависимости от округленных значений увеличений, нанесенных на рукоятках барабана.
| округленные значения увеличений, нанесенные на рукоятках барабана, крат | 0,6 | 1 | 2 | 4 | 7 |
| сторона квадрата 1 мм (соответствует величине на объекте) | 1,7 | 1,0 | 0,5 | 0,25 | 0,14 |
Для каждого опыта (для каждой концентрации) заполняется таблица вида:
| размер фракции | номер поля | ||||||
| 1 | 2 | 3 | 4 | 5 | |||
| деления | Ri, м | ||||||
После этого по уравнениям (4.12 - 4.15) рассчитываются средние радиусы частиц и коэффициент полидисперсности системы. Способы усреднения могут быть различными, в зависимости от того, какие параметры полидисперсной системы и заменяющей ее монодисперсной системы предполагаются одинаковыми (число частиц, поверхность, масса или объем). Наиболее часто используют следующие виды усреднения:
|
|
|
Ø среднечисленный радиус Rn (одинаковое число частиц)
, (4.12)
Ø среднеповерхностный Rs (одинаковая суммарная поверхность)
, (4.13)
Ø среднемассовый Rm (одинаковая общая масса или объем частиц)
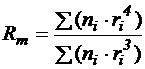, (4.14)
где ni - число частиц данной фракции с радиусом Ri;
åni - суммарное число частиц в системе.
Отношение:
(4.15)
называется коэффициентом полидисперсности. Чем больше разброс частиц по размерам, тем меньше kп.
Затем рассчитываются и строятся интегральные и дифференциальные кривые распределения частиц по числу, поверхности и массе.
Для нахождения функций распределения по размерам определяется процентное содержание числа частиц каждой фракции по отношению:
Ø к общему количеству частиц:
, (4.16)
Ø к их общей поверхности:
, (4.17)
Ø к их общему объму (массе):
(4.18)
|
|
|
Зависимости Qn = f(r), Qs = f(r), Qm = f(r) являются интегральными кривыми численного, поверхностного и массового распределения частиц по размерам. Каждая точка интегральной кривой характеризует процентное содержание (поверхность, объем) частиц, обладающих размерами данного и больших радиусов. Дифференциальные кривые численного, поверхностного и массового распределения представляют собой зависимости плотности распределения частиц по размерам: dQn / dr = f(r), dQs / dr = f(r), dQm / dr = f(r). Для получения этих зависимостей графически дифференцируют интегральные кривые распределения.
Степень агрегации частиц αn определяется по формуле (4.1). Также рассчитываются коэффициент формы флокул y по формуле (4.6).
Полученные данные вносят в таблицу 4.2.
Таблица 4.2
Результаты гранулометрического анализа суспензии
каолина полимерными флокулянтами
| № п/п | Концентрация флокулянта Сф, мг/л | Rn·105, м | RS·105, м | Rm·105, м | Kп | αn | y | |
| 1 2 3 4 5 6 | 0 0,1 0,3 0,5 1,0 2,0 |
Задание:написать формулу полимера, рассчитать гранулометрические характеристики суспензии, определить их зависимость от концентрации флокулянта.
Отчет должен содержать таблицу с полученными и рассчитанными данными, графики зависимостей Rn=f(Сф), Кп=f(Сф), а также рассчитанные интегральные и дифференциальные кривые численного распределения, сделать вывод о флокулирующем действии полимера.
|
|
|
Лабораторная работа № 8
Дата добавления: 2018-06-01; просмотров: 498; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!