Ou - общий уровень эмпатии учащихся

⇐ ПредыдущаяСтр 2 из 2

Дисципл.

Ou - общий уровень эмпатии учащихся

16,9 Дисципл.

16,5

Не дисципл.

18,7

Не дисципл.

По результатам выполненных вычислений мы можем сделать некоторые выводы о существовании различий по психологическим признакам между дву- мя (или более) выборками испытуемых.

Степень выявленного различия между средними желательно также оце- нивать, опираясь на содержательные критерии. Наиболее распространено для этого использование сигмы (σ). Разницу между двумя значениями в одну сигму и более можно считать достаточно выраженной. Если сигма (σ) подсчитана для ряда значений n более 35, то достаточно выраженной можно рассматривать разницу и в 0,5σ.

Помимо этого, среднее квадратическое отклонение обладает и другими чрезвычайно полезными свойствами, из которых хорошо запомнить одну важ- ную формулу, в которую входит среднее квадратическое отклонение. Предпо- ложим, что нам известны среднее значение и среднее квадратическое отклоне- ние для определенного набора данных. Умножьте среднее квадратическое от- клонение на 1,96. Вычтите полученный результат из среднего значения и запи- шите разность. Теперь прибавьте результат умножения (то есть 1,96 × σ- среднее квадратическое отклонение) к среднему значению и также запишите ответ.

1) M – 1,96σ ; 2) M + 1,96σ

Вы получили границы диапазона, в который попадают 95 % всех резуль- татов из вашего набора. Любые результаты, большие или меньшие этих край- них значений, являются относительно редкими, поскольку они встречаются только в 5 % всех случаев. По этой причине в большинстве психологических журналов требуется, чтобы в описании представленных к публикации данных присутствовало не только среднее значение, но и среднее квадратическое от- клонение - это позволит читателям оценить вариабельность обсуждаемых дан- ных, а также быстро рассчитать наиболее вероятный разброс результатов

Таким образом, сравнительный анализ первичных статистик является од- ним из распространенных методов обобщения данных. Он предусматривает их описание с помощью какой-либо меры центральной тенденции (обычно ис- пользуется среднее значение) и какой-либо оценки вариабельности (обычно ис- пользуется среднее квадратическое отклонение). Оценка вариабельности пока- зывает, насколько хорошо среднее значение отражает свойства рассматривае- мой выборки результатов. Однако, при этом предполагается, что данные рас- пределяются по нормальному закону. Это условие соблюдается в большинстве случаев, с которыми обычно сталкиваются исследователи, однако не во всех.

В тоже время, для ответственных выводов о том, насколько велика раз- ница между значениями и для того чтобы иметь возможность представить эти обобщения как определенные тенденции и распространить их на всю генераль- ную совокупность (популяцию) в целом, лучше использовать более строгие существующие статистические критерии. Которые используются для определе- ния уровня достоверности (статистической значимости) выявляемых разли- чий или связи.

Рассмотрим методы статистического вывода наиболее простые, надежные и чаще используемые из них. Но прежде, уточним некоторые понятия, которые

используются при применении данных методов. Это понятие статистических критериев, уровень достоверности различий или уровень статистической зна- чимости.

Понятие статистической значимости и статистического критерияВ любой научно-практической ситуации эксперимента (обследования) исследователи могут исследовать не всех людей (генеральную совокупность, популяцию), а только определенную выборку. Например, даже если мы иссле- дуем относительно небольшую группу людей, например больных, страдающих определенной болезнью, то и в этом случае весьма маловероятно, что у нас имеются соответствующие ресурсы или необходимость тестировать каждого человека, болеющего этой болезнью. Вместо этого обычно тестируют выборку из популяции, поскольку это удобнее и занимает меньше времени. В таком слу- чае, откуда нам известно, что результаты, полученные на выборке, представля- ют всю группу? Или, если использовать профессиональную терминологию, можем ли мы быть уверены, что наше исследование правильно описывает всю

популяцию, выборку из которой мы использовали?

Чтобы ответить на этот вопрос, необходимо определить статистическую значимость результатов тестирования. Статистическая значимость (Signifi- cant level, сокращенно Sig.), или p-уровень значимости (p-level) - это вероят- ность того, что данный результат правильно представляет популяцию, выборка из которой исследовалась. Отметим, что это только вероятность - невозможно с абсолютной гарантией утверждать, что данное исследование правильно опи- сывает всю популяцию. В лучшем случае по уровню значимости можно лишь заключить, что это весьма вероятно. Поэтому неизбежно встает следующий во- прос: каким должен быть уровень значимости, чтобы можно было считать дан- ный результат правильной характеристикой популяции?

Например, при каком значении вероятности вы готовы сказать, что таких шансов достаточно, чтобы рискнуть? Если шансы будут 10 из 100 или 50 из

100. А что если эта вероятность выше? Что можно сказать о таких шансах, как 90 из 100, 95 из 100 или 98 из 100? Для ситуации связанной с риском этот вы- бор довольно проблематичен, ибо зависит от личностных особенностей челове- ка.

В психологии же традиционно считается, что 95 или более шансов из 100 означают, что вероятность правильности результатов достаточна высока для того, чтобы их можно было распространить на всю популяцию. Эта цифра установлена в процессе научно-практической деятельности - нет никакого за- кона, согласно которому следует выбрать в качестве ориентира именно ее (и действительно, в других науках иногда выбирают другие значения уровня зна- чимости).

В психологи оперируют этой вероятностью несколько необычным обра- зом. Вместо вероятности того, что выборка представляет популяцию, указыва- ется вероятность того, что выборка не представляет популяцию. Иначе говоря, это вероятность того, что обнаруженная связь или различия носят случайный характер и не являются свойством совокупности. Таким образом, вместо того

чтобы утверждать, что результаты исследования правильны с вероятностью 95 из 100, психологи говорят, что имеется 5 шансов из 100, что результаты непра- вильны (точно так же 40 шансов из 100 в пользу правильности результатов означают 60 шансов из 100 в пользу их неправильности). Значение вероятности иногда выражают в процентах, но чаще его записывают в виде десятичной дро- би. Например, 10 шансов из 100 представляют в виде десятичной дроби 0,1; 5

из 100 записывается, как 0,05; 1 из 100 - 0,01. При такой форме записи гранич- ным значением является 0,05. Чтобы результат считался правильным, его уро- вень значимости должен быть ниже этого числа (вы помните, что это вероят- ность того, что результат неправильно описывает популяцию). Чтобы покон- чить с терминологией, добавим, что «вероятность неправильности результата» (которую правильнее называть уровнем значимости) обычно обозначается ла- тинской буквой – p. В описание результатов эксперимента обычно включают резюмирующий вывод, такой как «результаты оказались значимыми уровне достоверности (p < 0,05)». В переводе на обычный язык это означает, что веро- ятность неправильности результатов (p) менее 0,05 (то есть меньше 5 %).

Таким образом, уровень значимости (p) указывает на вероятность того, что результаты не представляют популяцию. По традиции в психологии счита- ется, что результаты достоверно отражают общую картину, если значение p меньше 0,05 (то есть 5 %). Тем не менее, это лишь вероятностное утверждение, а вовсе не безусловная гарантия. В некоторых случаях этот вывод может ока- заться неправильным. На самом деле, мы можем подсчитать, сколь часто это может случиться, если посмотрим на величину уровня значимости. При уровне значимости 0,05 в 5 из 100 случаев результаты, вероятно, неверны. На первый взгляд кажется, что это не слишком часто, однако если задуматься, то 5 шансов из 100 - это то же самое, что 1 из 20. Иначе говоря, в одном из каждых 20 слу- чаев результат окажется неверным. Такие шансы кажутся не особенно благо- приятными, и исследователи должны остерегаться совершения ошибки первого рода. Так называют ошибку, которая возникает, когда исследователи считают, что обнаружили реальные результаты, а на самом деле их нет. Противополож- ные ошибки, состоящие в том, что исследователи считают, будто они не обна- ружили результата, а на самом деле он есть, называют ошибками второго рода. Эти ошибки возникают потому, что нельзя исключить возможность не- правильности проведенного статистического анализа. Вероятность ошибки за- висит от уровня статистической значимости результатов. Мы уже отмечали, что, для того чтобы результат считался правильным, уровень значимости дол- жен быть ниже 0,05. Разумеется, некоторые результаты имеют более низкий уровень, и нередко можно встретить результаты с такими низкими p, как 0,001 (значение 0,001 говорит о том, что результаты могут быть неправильными с ве- роятностью 1 из 1000). Чем меньше значение p, тем тверже наша уверенность в

правильности результатов [63, c. 266-267].

В таблице 7.2 приведена традиционная интерпретация уровней значимо- сти о возможности статистического вывода и обосновании решение о наличии связи (различий).

Таблица 7.2 - Традиционная интерпретация уровней значимости, используемых в психологии.

Уровень значимости	Возможный статистический вывод
p > 0,1	«Статистически достоверные различия не обнаружены»
p < 0,1	«Различия обнаружены на уровне статистической тенден- ции»
p < 0,05	«Обнаружены статистически достоверные (значимые) раз- личия»
p < 0,01	«Различия обнаружены на высоком уровне статистической значимости»
p < 0,001	«Различия обнаружены почти на абсолютном уровне стати- стической значимости»

На основе опыта практических исследований рекомендуется, чтобы из- бежать, по возможности, ошибок I и II рода при ответственных выводах следу- ет принимать решения о наличии различий (связи), ориентируясь на уровень p<0,01, или на вычисленный статистический критерий для меньшего числа n признака.

Статистический критерий (Statistical Test) – это инструмент определе- ния уровня статистической значимости. Это решающее правило, обеспечиваю- щее принятие истиной и отклонение ложной гипотезы с высокой вероятностью1 (Суходольский Г.В., 1972, с. 291).

Статистические критерии обозначают также метод расчета определенного числа и само это число. Все критерии используются с одной главной целью: определ~~ить~~ ~~уровень~~ значимости анализируемых с их помощью данных (то есть вероятность того, что эти данные отражают истинный эффект, правильно пред- ставляющий популяцию, из которой сформирована выборка).

Некоторые критерии можно использовать только для нормально распре- деленных данных (и, если признак измерен по интервальной шкале), эти крите- рии обычно называют параметрическими. С помощью других критериев мож- но анализировать данные практически с любым законом распределения, и их называют непараметрическими критериями.

1 В настоящем учебном пособии мы подробно не рассматриваем проблему статисти- ческих гипотез (нулевой – H0 и альтернативной – H1) и принимаемые статистические реше- ния, поскольку это студенты-психологи изучают отдельно по дисциплине «Математические методы в психологии». Кроме того, необходимо отметить, что при оформлении исследова- тельского отчета (курсовой или дипломной работы, публикации) статистические гипотезы и статистические решения, как правило, не приводятся. Обычно при описании результатов указывают критерий, приводят необходимые описательные статистики (средние, сигмы, ко- эффициенты корреляции и т. д.), эмпирические значения критериев, степени свободы и обя- зательно p-уровень значимости. Затем формулируют содержательный вывод в отношении проверяемой гипотезы с указанием (обычно - в виде неравенства) достигнутого или не до- стигнутого уровня значимости.

Параметрические критерии

Критерии, включающие в формулу расчета параметры распределения, то есть средние и дисперсии (t-критерий Стьюдента, критерий F Фишера и др.).

Непараметрические критерии

Критерии, не включающие в формулу расчета параметров распределения и ос- нованные на оперировании частотами или рангами (критерий Q Розенбаума, критерий U Манна-Уитни и др.).

Например, когда мы говорим, что достоверность различий определялась по t-критерию Стьюдента, то имеется в виду, что использовался метод t-критерия Стьюдента для расчета эмпирического значения, которое затем сравнивается с табличным (критическим) значением.

По соотношению эмпирического (нами вычисленного) и критического значения критерия (табличного) мы можем судить о том, подтверждается или опровергается наша гипотеза. В большинстве случаев для того, чтобы мы признали различия значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, критерий Манна-Уитни или критерий знаков), в которых мы должны придерживаться противоположного правила.

Обратите внимание:

В некоторых случаях расчетная формула критерия включает в себя количество наблюдений в исследуемой выборке, обозначаемое как - n. По специальной таблице мы определяем, какому уровню статистической значимости различий соответствует данная эмпирическая величина. В большинстве случаев, одно и то же эмпирическое значение критерия может оказаться значимым или незначимым в зависимости от количества наблюдений в исследуемой выборке

(n) или от так называемого количества степеней свободы, которое обозначается как – v (v) или как dƒ (иногда – d) .

Зная n или число степеней свободы, мы по специальным таблицам (основ- ные из них приводятся в приложении) можем определить критические значения критерия и сопоставить с ними полученное эмпирическое значение. Обычно это записывается так: «при n = 22 критические значения критерия составляют t St = 2, 07» или «при v (d) = 2 критические значения критерия Стьюдента состав- ляют t St = 4, 30» и т.п.

Обычно, предпочтение оказывается все же параметрическим критериям, и мы придерживаемся этой позиции. Считается, что они более надежны, и с их помощью можно получить больше информации и провести более глубокий анализ, чем с использованием непараметрических критериев. Что же касается сложности математических вычислений, то при использовании компьютерных программ эта сложность исчезает (но, появляются некоторые другие, впрочем, вполне преодолимые).

Оценка достоверности отличий по t-критерию Стьюдента

Наиболее часто в психологическом исследовании встречается задача вы- явления различий между двумя или более группами признаков. Выявление та- ких различий на уровне средних арифметических мы уже рассмотрели выше в процедуре анализа первичных статистик. Однако, возникает вопрос насколько эти различия достоверны и можно ли их распространить (экстраполировать) на всю популяцию. Для решения этой задачи чаще всего используется (при усло- вии нормального или близкого к нормальному распределения) t-критерий (или критерий Стьюдента). Этот критерий предназначен для того, чтобы выяснить, на сколько достоверно различаются показатели одной выборки испытуемых от другой (например, когда испытуемые получают в результате тестирования од- ной группы более высокие баллы, чем представители другой). Это параметри- ческий критерий, имеющий две основные формы. Первая из них - несвязанный t-критерий (который также называют непарным t-критерием) - предназначен для того, чтобы выяснить, имеются ли различия между оценками, полученными при использовании одного и того же теста для тестирования двух групп, со- ставленных из разных людей.

Например: это может быть сравнение уровня интеллекта или нервно- психической устойчивости, тревожности «успешных» учащихся и «отстаю- щих» или сравнение по этим признакам учащихся разных классов, возрастных групп, социальных уровней и т.д. Это могут быть разнополые, различных наци- ональностей выборки, а также подвыборки в исследуемых выборках, выделен- ные по определенному признаку.

Мы на это указывали, когда говорили о независимых переменных, «L»,

«Q», и «T»- данных, на основании которых возможно выделение подвыборок в основной выборке исследуемых.

Критерий называется «несвязанным», потому что сравниваемые группы составлены из разных людей. Связанный t-критерий (который иногда называют парным t-критерием) предназначен для сравнения показателей двух групп, между членами которых существует специфическая связь. Это означает, что каждому члену первой группы соответствует какой-либо член второй группы, который похож на него по какому-то параметру, интересующему исследовате- ля. Чаще всего сравниваются параметры одних и тех же людей до и после опре- деленного события или воздействия (например, в процессе проведения лонги- тюдного исследования или формирующего эксперимента). Поэтому данный критерий используется для сравнения показателей одних и тех же людей до и после обследования, эксперимента или прошествии некоторого времени.

В случаях, когда данные не подчиняются нормальному закону распреде- ления, используются непараметрические критерии, эквивалентные t-критериям. Это критерий Манна-Уитни, который эквивалентен непарному t- критерию, и двухвыборочный критерий Вилкоксона, эквивалентный парному t-критерию.

С помощью t-критериев и их непараметрических эквивалентов можно лишь сравнивать результаты двух групп, полученные с использованием одного и того же теста. Однако в некоторых случаях возникает необходимость сравне- ния нескольких групп или оценок нескольких видов. Это можно сделать по-

этапно, разбив задачу на несколько пар сравнений (например, если надо срав- нить группы А, Б и В по результатам тестов Х и У, то можно с помощью t- критерия сначала сравнить группы А и Б по результатам теста X, потом А и Б по результатам теста У, А и В по результатам теста Х и так далее). Однако это очень трудоемкий метод; кроме того, по некоторым причинам, в объяснение которых мы не будем здесь углубляться, при его использовании резко возраста- ет вероятность совершения ошибки первого рода. Поэтому необходим более сложный метод, метод дисперсионного анализа, который требует использова- ния прикладных программ и силу определенной сложности нами не рассматри- вается

И так, рассмотрим более подробно метод оценки достоверность различий средних арифметических по достаточно эффективному параметрическому критерию Стьюдента,который предназначен для решения одной из наиболее часто встречающихся задач при обработке данных - выявления достоверности различий между двумя, или более, рядами значений.

Данная оценка часто необходима при сравнительном анализе полярных групп. Эти группы можно выделить, учитывая различную выраженность опре- деленного целевого признака (характеристики) изучаемого явления. Какими критериями при этом руководствоваться мы указывали выше. Обычно анализ начинают с подсчета первичных статистик выделенных групп, затем оценивают достоверность отличий. Он вычисляется по формуле:

t St =

M1 - M 2

;

2 + m 2

(7.5)

где M1 и M2 - значения сравниваемых средних арифметических; t St - ве- личина вычисленного эмпирического критерия, который необходимо срав- нивать с критическим; m1 и m2 - соответствующие величины статистиче- ских ошибок средних арифметических.

Значения критерия Стьюдента для трех уровней доверительной (стати- стической) значимости (p) приведены в приложении 4. Число степеней свободы определяется по формуле d = v = n1 + n2 - 2, где n и n - объемы сравниваемых выборок. С уменьшением объемов выборок (n < 10) критерий Стьюдента стано- вится чувствительным к форме распределения исследуемого признака в гене- ральной совокупности. Поэтому в сомнительных случаях рекомендуется ис- пользовать непараметрические методы или сравнивать полученные значения с критическими (приведенными в таблице) для более высокого уровня значимо- сти.

Решение о достоверности различий принимается в том случае, если вы- численная величина tSt превышает табличное значение для данного числа сте- пеней свободы (d (v)). В тексте публикации или научного отчета указывают наиболее высокий уровень значимости из трех: p<0.05; p<0.01; p<0.001.

Приведенная формула проста. Используя ее, можно с помощью бытового калькулятора с памятью вычислить t-критерий без промежуточных записей. Однако, на наш взгляд, целесообразнее вычислять его, используя компьютер- ные программы. Алгоритм вычисления в программе Excel мы рассмотрим ни- же.

Однако, следует помнить, что при любом численном значении критерия достоверности различия между средними этот показатель оценивает не степень выявленного различия (она оценивается по самой разности между средними), а лишь статистическую достоверность его, т.е. право распространять полученный на основе сопоставления выборок вывод о наличии разницы на все явление (весь процесс) в целом. Низкий вычисленный критерий различия не может служить доказательством отсутствия различия между двумя признаками (яв- лениями), ибо его значимость (степень вероятности) зависит не только от вели- чины средних, но и от численности сравниваемых выборок. Он говорит не об отсутствии различия, а о том, что при данной величине выборок оно статисти- чески недостоверно: слишком велик шанс, что разница при данных условиях определения случайна, слишком мала вероятность ее достоверности [25, c. 70].

Алгоритм вычисления t-критерия Стьюдента в программе Excel:

При условии нормального или близкого к нормальному распределения, сравниваются две выборки или подвыбоки (из основной выборки), различаю- щиеся по какому-либо показателю (независимой переменной).

Для выборок это могут быть мужчины и женщины (если ставится задача выявления гендерных различий), лица подросткового и юношеского возраста (при выявлении психологических особенностей возрастного развития) и т. д.

Если выборка одна, то одной из задач исследования может быть выявле- ние психологических особенностей, характеристик, присущих «успешным» и

«не успешным» в данной выборке по каким-либо психологическим характери- стикам. Решение этого рода задач мы и рассмотрим в качестве примера.

В любом случае, в выборках, подвыборках вычисляются первичные ста- тистики: M, σ, n, m.

Выделения подвыборок в основной выборке осуществляется при помощи функции «Сортировка». Необходимо отсортировать выборку по какому-либо признаку. На примере эмпирических данных нашей таблицы это могут быть:

1) интегральная шкала опросника МЛО «Адаптивность» - ЛАП (личност- ный адаптационный потенциал) и основные подшкалы: ПР (поведенческая ре- гуляция, нервно-психическая устойчивость), КК (коммуникативные качества), МН (моральная нормативность);

2) шкалы опросника «Спилбергера-Ханина» - РТ (реактивная тревож- ность – ситуативная) и ЛТ (личностная тревожность – как черта личности);

3) интегральная шкала интеллектуальной батареи – Балл.

По каждой из этих шкал мы можем выделить группы «успешных» и «не успешных» по данному признаку и выявить различаются они на достоверно значимом уровне или не различаются по остальным психологическим характе- ристикам.

Пример:

Гипотеза (предположение): учащиеся с более высоким уровнем развития основных познавательных процессов отличаются от учащихся с более низким уровнем развития познавательных психических процессов по ряду личностных характеристик.

Задача: выделить группы «успешных» и «не успешных» учащихся по уровню развития основных познавательных психических процессов с целью дальнейшего выявления различий между ними по личностным характеристи- кам.

Алгоритм сортировки данных сводной таблицы исследования студентов- психологов по шкале «Балл» (Рисунок 7.17).

Открываем Excel «лист 1» сводной таблицы. Выделяем данные для сор- тировки: начиная от первой ячейки шкалы наименований признаков (в данном примере – A3) и заканчивая последней ячейкой численного показателя в по- следнем столбце признаков (в данном примере – P29). В меню выбираем «Дан- ные»> «Сортировка»> «Сортировать по …»> «Балл» > ◙ «по возрастанию» (или «убыванию») > ОК.

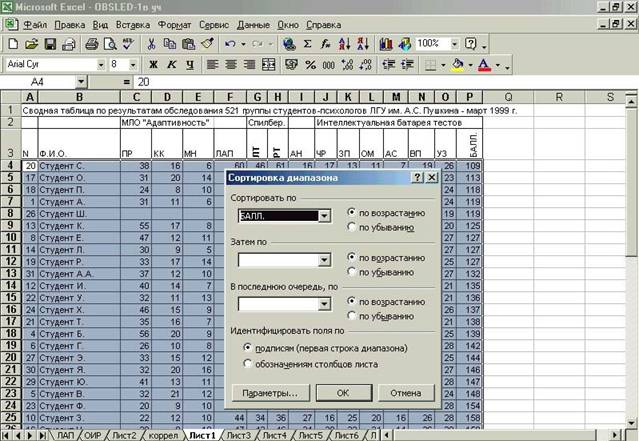
Рисунок 7.17 – Сортировка по шкале «Балл» (Р)

Данные отсортированы по возрастанию, начиная от меньшего показателя признака к большему. Затем начинается творческая работа исследователя. По- скольку выборка одна и подчиняется закону нормального распределения при- знака, то следует в ней определить крайние границы «успешных» и «не успеш-

ных» по интеллекту. В целом, можно придерживаться правила, что 50% при- знаков от средней арифметической составляют популяционную норму, а следо- вательно, из расчетов должны быть исключены. Однако, в практике эти грани- цы можно варьировать, но в разумных пределах, при определении подвыборок в основной выборке.

Выделим в качестве «не успешных» выборку с параметрами P 4 : P 12 (т.е. n1 = 9), а «успешных» - P 24 : P 29 (т.е. n2 = 6). Вычислим для каждой этой выборки отдельно M, σ (S), n, m, придерживаясь алгоритма, указанного раннее для вычисления первичных статистик, используя «Вставку функций» (Рисунок 7.18).

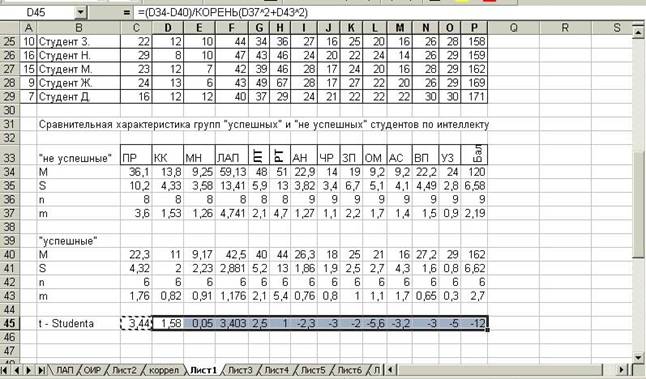
Рисунок 7.18 – вычисление первичных статистик по подвыборкам

Будьте внимательны! Вы определяете параметры выборок «успешных» и

«не успешны» по столбцу «P» («Балл»). Но вычисления будете проводить в столбце первого признака под таблицей – «С». Поэтому параметры выборки

«не успешных» будут С 4 : С 12, а «успешных» - С 24: С 29. (см. Рисунок 7.18). После того как вычислены первичные статистики по выборкам «успешных» и

«не успешных», переходим к вычислению t-критерия Стьюдента.

Алгоритм вычисления t-критерия Стьюдента:

Курсор помещаем в ячейку С 45 (см. Рисунок 7.18) и на клавиатуре небираем формулу вычисления t-критерия. Напоминаем как она выглядит и ее вид при введении через клавиатуру в программе Excel.

t St =

M1 - M 2

;

2 + m 2

= (С 34 – С 40)/корень(C 37^2 + C 43^2)

Обращаем внимание, формула набирается только в английском шрифте, за исключение слова «корень», после чего не забудьте вновь переключиться на английский. Будьте внимательны в соблюденнии знаков и их порядка.

С 34 –координаты М1 – «не успешных».

С 40 –координаты М2 – «успешных».

^- показатель степени в которую возводится значение в данной ячейке. Набирается следующим образом: нажимаем одновременно две клавиши

«Shift + 6» и появляется значок ^показателя степени. Затем, набираем квадрат числа – 2.

C 37 –координаты m1 – «не успешных».

C 43 –координаты m1 – «не успешных».

Далее > ОК, появляется вычисленное значение t-критерия для значений признака данного столбца – 3,44. Копируем эту ячейку. Выделяем область втавки по другими сталбцами признаков – «Вставить» > появляются вычисленные значения для других столбцов признаков.

Затем обращаемся к таблице «Квантили t-распределения Стьюдента для доверительной вероятности (1-а = 0,95; 0,99; 0,999)» (см. Приложение 4). Вычисляем число степеней свободы по формуле v = d = n1 + n2 – 2,для нашего примера v =6 + 9 – 2 = 13. Выписывем критические значения для p<0,05 оно равно 2,160; для p<0,01 равно 3,012; для p<0,001 равно 4,221. Сравниваем данные значения с эмпирическими, полученными в результате вычислений и оформляем их в виде таблицы. Например:

Таблица 7.3 - Оценка достоверности отличий «успешных» и «не успешных» студентов 521 группы ЛГУ по уровню развития познавательных психических процессов

	ПР	КК	МН	ЛАП	ЛТ	РТ	АН	ЧР	ЗП	ОМ	АС	ВП	УЗ	Бал
t-Studenta	3,44	1,58	0,054	3,40	2,49	1,05	-2,32	-3,36	-2,14	-5,6	-3,19	-3,03	-4,96	-12

Возможен и другой вариант таблицы более информативный:

Таблица 7.4 - Оценка достоверности отличий «успешных» и «не успешных» студентов 521 группы ЛГУ по уровню развития познавательных психических процессов

№	Психологический признак	«успешные» (n = 6)		«не успешные» (n = 9)		t- Stud	p
		M±m	σ	M±m	σ
1.	Поведенческая регуляция (ПР)	22,3 ± 1,76	10,1	36,1 ± 3,6	10,2	3,44	p < 0,01

2.	Коммуникативные качества (КК)	11,0 ± 0,82	2,0	13,8 ± 1,53	4,33	1,58
3.	Моральная нормативность (МН)	9,17 ± 0,91	2,23	9,25 ± 1,26	3,58	0,05
4.	Личностныйадапта- ционный потенциал	42,5 ± 1,18	2,89	59,13 ± 4,74	13,41	3,40	p < 0,01
5.	Личностная тревожность (ЛТ)	40,33 ± 2,12	5,20	47,75 ± 2,09	5,92	2,49	p<0,05
6.	Реактивная тревожность (РТ)	43,67 ± 5,36	13,13	51,13 ± 4,68	13,23	1,05
7.	Аналогии	26,33 ± 0,76	1,86	22,89 ± 1,27	3,82	2,32	p < 0,05
8.	Числовые ряды	18,17 ± 0,79	1,94	13,56 ± 1,12	3,36	3,36	p < 0,01
9.	Зрительная память	24,67 ± 1,02	2,50	19,44 ± 2,22	6,65	2,14
10.	Образное мышление	20,67 ± 1,12	2,73	9,22 ± 1,71	5,14	5,60	p<0,001
11.	Арифметический счет	16,33 ± 1,75	4,27	9,22 ± 1,38	4,15	3,19	p < 0,01
12.	Вербальная память	27,17 ± 0,65	1,60	22,22 ± 1,50	4,49	3,03	p < 0,01
13.	Установл. закономерн	28,83 ± 0,30	0,75	23,89 ± 0,94	2,85	4,96	p<0,00
14.	Интегральный балл	162,2 ± 2,70	6,62	120,4 ± 2,19	6,58	12,0	p<0,00

Мы видим, что по всем субтестам (методикам) интеллектуальной батареи (кроме «зрительная память») группы «успешных» и «не успешных» студентов значимо различаются на уровне p<0,05. По методикам «Числовые ряды» (ЧР),

«Арифметический счет» (АС), «Вербальная память» (ВП) студенты различаются на уровне p<0,01, а по методикам «Образное мышление» (ОМ) и

«Установление закономерностей» (УЗ) на уровне p<0,001, не говоря уже об интегральной шкале «Балл» на основании которой мы выделяли подгруппы.

Анализ личностных характеристик показывает, что «успешные» студенты значимо различаются от «не успешных» по таким признакам, как уровень поведенческой регуляциии (p<0,01), личностному адаптационному потенциалу (p<0,01), личностной тревожности (p<0,05). И это вполне закономерно, поскольку в основе адаптивных возможностей лежат такие психологические характеристики как нервно-психическая устойчивость, повышенная тревожность, наличие определенных акцентуаций характера, адекватность самооценки и некоторые другие, которые оказывают несомненное влияние на особенности протекания познавательных психических процессов. В тоже время, по таким характеристикам как коммуникативные качества, общительность, коммуникабельность, моральная нормативность и ситуативная тревожность, выделенные выборки студентов значимо не различаются. Значит эти характеристики оказывают меньшее влияние на эффективность интеллектуальной деятельности.

Однако, данный пример обобщений и сделанные выводы нельзя экстраполировать на всю популяцию в целом. Поскольку выборка единична, малочисленна и ограничена, то мы не вправе сделать, например, такой обощающий вывод: что студенты, которые выделяются высоким уровнем развития познавательных психических процессов, обладают или имеют высокие адаптивные возможности. Не совсем верен буден и обратный вывод: наличие высоких адаптивных возможностей не есть прямое свидетельство или причина успехов в сфере интеллектуальной деятельности.

Закономерные причинные взаимосвязи, тенденции здесь несомненно присутствуют. Но исследования по данной проблеме показывают, что все обстоит не так просто и прямолинейно. Об этом мы еще будем говорить ниже, при рассмотрении метода корреляционного анализа. Пока же мы предостерегаем вас от скоропалительных обобщений, особенно в случае когда на малочисленных выборках и при использовании одного метода получены достаточно убедительные результаты.

Корреляционный анализ

Мы рассмотрели t-критерий предназначенный, в основном, для сравнения результатов различных групп испытуемых (при условии нормального распре- деления и данных, представленных в нормированных шкалах). Другой доволь- но часто встречающейся задачей психологического исследования является вы- явление взаимосвязей между двумя или более наборами данных. Одной из про- стейших форм выявления такой связи является корреляция.

Корреляционный анализ дает возможность точной количественной оценки степени согласованности изменений (варьирования) двух и более при- знаков. Степень согласованности изменений характеризует теснота связи - аб- солютная величина коэффициента корреляции.

Наличие корреляции между двумя результатами, в сущности, означает, что при изменении одного результата другой также изменяется - таким обра- зом, между результатами существует, выявляется связь. Если значение некото- рой величины может изменяться, то такую величину называют переменной. Корреляция между двумя переменными может быть положительной или отри- цательной. Положительной корреляцией называется такая связь между пере- менными, когда значения обеих переменных возрастают или убывают пропор- ционально: с уменьшением (увеличением) одной уменьшается (увеличивается) другая. Простым примером положительной корреляции является связь между ростом и весом человека - с возрастанием роста возрастает и вес, и, как прави- ло, люди высокого роста имеют больший вес, чем люди маленького роста. В случае отрицательной корреляции, связь является обратно пропорциональной: возрастание одной переменной сопровождается убыванием другой (например, температура воздуха и количество надетой одежды - чем теплее на улице, тем меньше одежды мы надеваем).

Важно отметить другое, что, корреляция еще не означает наличия при-чинно-следственной связи. Наличие корреляции говорит о том, что между дву- мя переменными существует связь, но не о том, что одна из переменных явля- ется причиной, а другая - следствием. Существование причинно-следственной связи устанавливается другими методами.

Поэтому, достаточно рискован содержательный вывод о причинно- следственной зависимости между изучаемыми явлениями только на основании статистической значимости связи между соответствующими признаками (т.е. на основании коэффициента корреляции). Конечно, статическая связь между признаками - это необходимое, но не достаточное условие причинно- следственной связи между ними. Утверждение о том, что явление А есть при- чина явления В, справедливо, если одновременно выполняются три условия (Кэмпбелл Д. Модели экспериментов в социальной психологии и прикладных исследованиях. М., 1980):

а) явления А и В статистически связаны; б) А происходит раньше В;

в) отсутствует альтернативная интерпретация появления В помимо А (другими словами - отсутствует общая причина С совместной изменчивости А и В).

Таким образом, применение корреляционного метода позволяет обосно- вать наличие только статистической связи - одного из трех признаков при- чинно-следственной связи [40, c. 108-109].

Но, вернемся к приведенному выше примеру с температурой воздуха и одеждой. Наличие связи между этими переменными не означает, что если мы снимем одежду, то температура воздуха повысится. Нам придется воспользо- ваться другими методами, чтобы показать, что в данном случае связь является односторонней и причиной изменения количества одежды, которую надевают люди, является изменение температуры воздуха. В других случаях связь между двумя переменными может быть обусловлена какой-либо третьей переменной, и корреляция просто отражает наличие чего-то общего между двумя перемен- ными и этой третьей. Для иллюстрации подобной ситуации часто приводят следующий пример: если бы у нас возникло странное желание измерить размер ступни школьников и оценить их знания по математике, то мы обнаружили бы положительную корреляцию между длиной ступни и оценками по математике.

Означает ли это, что математические способности зависят от размера но- ги или что у тех, кто делает успехи в математике, быстрее растут ноги? Конеч- но же нет - эта корреляция объясняется влиянием третьей переменной: а имен- но, возраста (чем старше ребенок, тем больше у него нога и тем лучше он раз- бирается в математике). Поэтому при интерпретации корреляции необходима осторожность [63, c. 271].

После того как выявлена положительная или отрицательная корреляция, необходимо установить, сколь тесной она является. На это указывает коэффи- циент корреляции, который обозначают буквой r, величина r варьирует в диапа- зоне от -1 до +1. В случае прямо пропорциональной зависимости одного при- знака от другого коэффициент корреляции равен единице (т.е. признак корре- лирует (связан) сам с собой). Отрицательный коэффициент корреляции, как указывалось выше, свидетельствует о разной направленности варьирования признаков: при изменении одного в сторону увеличения - другой уменьшается и обратно.

Когда статистическому анализу подвергаются данные, взятые из «реаль- ной жизни», то обычно выявляются корреляции с коэффициентами, находящи- мися в диапазоне между нулем (отсутствие корреляции) и единицей (идеальная корреляция), и чем ближе значение r к ±1, тем более тесной является связь. Значения r выражаются в десятичных дробях (например, - 0,23; + 0,5 и т. п.). При низких значениях r (обычно низкими считаются значения, не превышаю- щие 0,2 при n ≤ 30) корреляция, как правило, не является статистически значи- мой.

Нулевая величина коэффициента корреляции говорит об отсутствии вза- имосвязи между признаками, но такое встречается очень редко, ибо в сфере психических явлений все явления со всеми взаимосвязаны (в большинстве слу- чаев опосредованно и могут проявляться лишь на уровне тенденций). Это не требует доказательств. И вся проблема в том, на сколько тесна эта взаимосвязь, чем и какими факторами она опосредуется, от чего зависит, какими методами выявляется и каким образом учитывается в практической деятельности обуче-

ния, воспитания, формирования профессионально важных навыков, качеств, мастерства.

Рассматривая числовые значения коэффициентов корреляции, создается впечатление, будто значения r являются непосредственным показателем силы корреляции. Например, можно подумать, что поскольку при идеальной поло- жительной корреляции r (+1), то r = 0,7 соответствует 70 % идеальной корреля- ции (или, точно так же, что r = 0,4 соответствует 40 % идеальной отрицатель- ной корреляции). На самом же деле коэффициент корреляции - довольно об- манчивое число. Чтобы найти, какую процентную долю от идеальной корреля- ции составляет данное значение r, необходимо возвести его в квадрат, а резуль- тат умножить на 100. Если r = 0,7, то такая корреляция составляет 49 % от иде- альной (0,7 × 0,7 × 100 = 49). Точно так же отрицательная корреляция r = - 0,4 составляет 16 % от идеальной отрицательной корреляции. Поэтому «степень идеальности» корреляции может быть гораздо меньше, чем можно подумать, если судить по значению r [63, c. 271].

Статистики обычно не пользуются понятием «степени идеальности», а считают, что коэффициент корреляции r указывает на долю изменений одной переменной, которые можно предсказать по изменениям другой переменной. Существует много методов измерения корреляции, и выбор конкретного метода зависит от типа рассматриваемых данных.

Мы с вами рассмотрим алгоритм вычисления коэффициента корреляции Пирсона, который является мерой корреляции между двумя переменными, рас- пределенными по нормальному закону (например, для выявления взаимосвязи уровня развития интеллекта и адаптивных возможностей личности или связи между успеваемостью по математике и временем решения арифметической за- дачи и т.д.). Преимущество данного метода состоит в том, что на величину кор- реляции не влияет, то, в каких единицах измерения представлены признаки [40,

c. 72]. Недостатком метода является сложность математических вычислений особенно для больших массивов данных. Однако, этот недостаток вполне устраним применением прикладных программ (например, наиболее простая - Excel).

Непараметрическим эквивалентом этой оценки является коэффициент корреляции Спирмена (например, для сравнения порядка прихода к финишу од- них и тех же бегунов в двух забегах или выявления связи между успеваемостью по математике и временем решения арифметической задачи и т.д.). Преимуще- ство метода состоит в возможности проведения не очень сложных математиче- ских вычислений с использованием калькулятора для небольших по объему выборок. Недостатком метода являются ограничения налагаемые сложностью обработки значительных массивов данных и необходимости ранжирования ря- дов значений.

Алгоритм вычисления коэффициента корреляции Пирсона в программе Ex- cel.

Открываем Лист 1 сводной ведомости. Выбираем в меню «Сервис» >

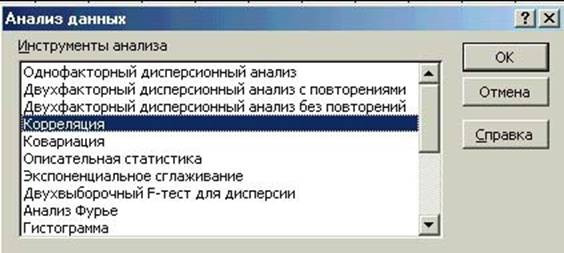«Анализ данных», появляется диалоговое окно «Анализ данных» (Рисунок 7.19).

Рисунок 7.19 – Диалоговое окно «Анализ данных», функция «Корреляция» Выбираем «Корреляция» >ОК. Появляется диалоговое окно «Корреля-

ция» (Рисунок 7.20).

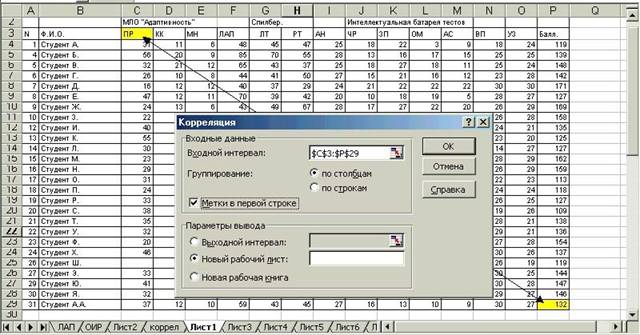
Рисунок 7.20 – Диалоговое окно «Корреляция» и входной интервал

Задаем Входной интервал(обозначен стрелкой). Для нашей таблицы это будет весь массив данных, включающий и шкалу наименований признаков: от первой ячейки наименования признака С 3(признак ПР – столбец С) до по-следнего численного значения в крайнем правом столбце P 29(признак Балл – столбец Р) по диагонали.

Далее выставляем: Группирование◙ по столбцам (задано автоматиче- ски); ◙ Метки в первой строке; ◙ Новый рабочий лист(задано автоматиче- ски) >ОК.

На новом рабочем листе появляется корреляционная матрица, которая имеет следую- щий вид (Рисунок 7.21).

ПР КК МН ЛАП ЛТ РТ АН ЧР ЗП ОМ АС ВП УЗ Балл.

ПР 1

КК 0,471 1

МН -0,08 0,366 1

ЛАП 0,909 0,752 0,274 1

ЛТ 0,674 0,428 -0,21 0,61 1

РТ 0,15 -0,07 -0,36 0,015 0,395 1

АН -0,26 -0,04 0,012 -0,22 0,128 0,018 1

ЧР -0,39 -0,23 -0,2 -0,42 -0,22 -0,11 0,334 1

ЗП -0,18 -0,23 -0,24 -0,26 -0,18 -0,22 -0,08 -0,02 1

ОМ -0,24 -0,11 0,147 -0,19 -0,3 -0,31 0,07 0,293 0,229 1

АС -0,43 0,114 0,027 -0,3 -0,03 0,058 0,326 0,34 0,072 0,296 1

ВП -0,01 0,087 0,531 0,137 -0,14 -0,32 0,115 -0,07 0,126 0,501 0,081 1

УЗ -0,48 -0,38 -0,01 -0,49 -0,26 -0,12 0,331 0,492 -0,08 0,553 0,327 0,164 1

Балл. -0,46 -0,18 0,07 -0,4 -0,27 -0,28 0,425 0,503 0,443 0,788 0,61 0,513 0,625 1

Рисунок 7.21 - Результаты корреляционного анализа данных студентов- психологов 521 группы ЛГУ по результатам обследования в марте 1999 г.

Данную корреляционную матрицу необходимо распечатать и вооружив- шись карандашами (фломастерами) приступить к ее анализу.

В каждой строке матрицы интеркорреляций представлены коэффициенты корреляции одного признака со всеми остальными в том порядке признаков, который был избран при составлении сводной таблицы данных. Матрица обыч- но содержит коэффициенты корреляции одной группы признаков с другой группой признаков того же пространства (всей совокупности) признаков. Стро- ки и столбцы матрицы обозначены наименованием признаков, в ячейках приве- дены коэффициенты корреляции одного признака с другим. Испытуемые и их порядковые номера из таблицы исходных данных в матрице интеркорреляций никак не представлены. Коэффициенты корреляции несут информацию только о тесноте связи между признаками и не дают никаких сведений ни об одном испытуемом.

Для эффективного использования вычисленных коэффициентов корреля- ции необходимо представить имеющуюся числовую информацию в наглядной форме. Прежде всего, необходимо выделить коэффициенты корреляции, вели- чина которых превышает критические значения для уровня доверительной ве- роятности (статистической значимости) p<0,05; p<0,01; p<0,001.

Критические значения коэффициента корреляции Пирсона приведены в приложении 6.

Целесообразно выделить коэффициенты корреляции, превышающие эти уровни значимости. Можно подчеркнуть коэффициенты с достоверностью 0.05 одной чертой или отметить одной звездочкой, с достоверностью 0.01 – двумя, а с достоверностью 0,001 - тремя. Удобно использовать и цветовое кодирование.

Если матрица большая, то даже выделение значимых коэффициентов не создает достаточной наглядности. Тогда к нижней части матрицы можно доба- вить еще несколько строк и записать в соответствующих клетках число значи-

мых коэффициентов в данном столбце: значимых на уровне p<0,05, на уровне p<0,01 и p<0,001, суммарное число значимых коэффициентов. Это лучше поз- волит увидеть иерархию признаков по числу значимых корреляционных связей.

Наглядное представление результатов корреляционного анализа

Следует сразу оговориться, что на нашем примере, поскольку выборка незначительна и число признаков ограничено табличное оформление данных выглядит не совсем эффектно и представительно. Но, в качестве примера, табличное представление имеющихся данных может быть оформлено следующим образом (Таблица 7.5).

Таблица 7.5 - Результаты корреляционного анализа связей личностных характеристик студентов-психологов 521 группы ЛГУ с уровнем развития основных познавательных психических процессов (n = 25)

Признак	ПР	КК	МН	ЛАП	ЛТ	РТ
Балл ОИР	-0,46	-0,18	0,07	-0,40	-0,27	-0,28
p	p<0,05	–	–	p<0,05	–	–

Примечание:

1. ПР – поведенческая регуляция

2. КК – комуникативные качества

3. МН – моральная нормативность

4. ЛАП – личностный адаптационный потенциал

5. ЛТ –личностная тревожность

6. РТ – реактивная тревожность.

В реальном психологическом исследовании и описании его результатов наглядность представления данных корреляционного анализа возрастает на несколько порядков.

В ряде случаев, для наглядности выявленных взаимосвязей используют корреляционные плеяды (Рисунок 7.22). И то, и другое представление данных корреляционного анализа вполне обоснованно. Ибо, форма в данном случае, мало зависит от содержания, однако, оценка и показательность содержания ваших исследований в немалой степени зависит от формы представления результатов.

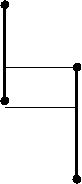
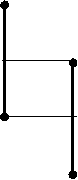
Например, вот как выглядит форма представления взаимосвязи компонентов эмпатийного потенциала учащихся с высоким и низким уровнем дисциплинированности в виде плеяды корреляционных связей:

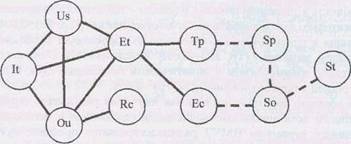
Высокодисциплинированные учащиеся

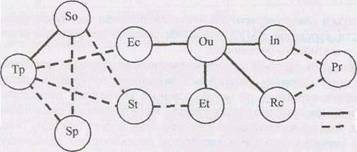
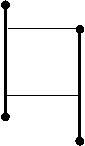
Низкодисциплинированные учащиеся

Рисунок 7.22 - Корреляционная плеяда компонентов эмпатийного потенциала учащихся с высоким и низким уровнем дисциплинированности

Примечание:

- прямая связь

- обратная связь

1. Sp - стремление к принятию

2. Sо - страх отвержения

3. Rс - рациональный канал эмпатии

4. Ec -эмоциональный канал

5. In - интуитивный канал

6. Us - установки способствующие или препятствующие эмпатии

7. Pr - проникающая способность

8. It – идентификация

9. Ou - общий уровень эмпатии

10. Et - эмпатическая тенденция

11. Тр - тенденция к присоединению

12. St - сензитивность к отвержению.

(Марютин В.А. Автореф. дис…канд. психол. наук. Психологические особенности взаимосвязи эмпатии и дисциплинированности у курсантов ВМУЗ радиоэлектронного профиля. СПб, 2004. – 24 с. – С. 15).

Расмотрим, какие выводы могут быть сделаны на основании анализа корреляционных связей, представленных на рисунке 7.21 и в таблице 7.5

Мы видим, что лишь в отношении двух признаков: уровня поведенческой регуляции (ПР) и личностного адаптационного потенциала (ЛАП), можно сделать заключения, что они связаны с функционированием некоторых познавательных психических процессов на достоверно значимом уровне (p<0,05). Такие психологические признаки как личностная тревожность (ЛТ) и реактивная тревожность (РТ - ситуативная), лишь только выходят на уровень доверительной значимости, а следовательно не являются решающими и оказывающими значимое влияние на протекание познавательных психических процессов. Тем более, такие психологические признаки как коммуникативные качества и моральная нормативность в очень слабой степени связаны с интеллектуальными функциями. Результаты данного обследования в большинстве своем соответствуют и подтверждают основные положения концепции адаптации личности к условиям учебно-профессиональной деятельности.

Непараметрические методы математической статистики

Непараметрические методы математической статистики используются в случаях, если распределение далекое от нормального и выборка незначительная (n<10).

Критерий Q Розенбаума 1

Назначение критерия

Критерий используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой из выбо- рок должно быть не менее 11 испытуемых.

Описание критерия

Это очень простой непараметрический критерий, который позволяет быстро оценить различия между двумя выборками по какому-либо признаку. Однако если критерий Q не выявляет достоверных различий, это еще не озна- чает, что их действительно нет.

В этом случае стоит применить F-критерий Фишера. Если же Q-критерий выявляет достоверные различия между выборками с уровнем значимости p<0,01, можно ограничиться только им и избежать трудностей применения дру- гих критериев.

Критерий применяется в тех случаях, когда данные представлены, по крайней мере, в порядковой шкале. Признак должен варьировать в каком-то диапазоне значений, иначе сопоставления с помощью Q -критерия просто не- возможны. Например, если у нас только 3 значения признака, 1, 2 и 3, - нам очень трудно будет установить различия. Метод Розенбаума требует, следова- тельно, достаточно тонко измеренных признаков.

Применение критерия начинаем с того, что упорядочиваем значения при- знака в обеих выборках по нарастанию (или убыванию) признака. Лучше всего, если данные каждого испытуемого представлены на отдельной карточке. Тогда ничего не стоит упорядочить два ряда значений по интересующему нас призна- ку, раскладывая карточки на столе. Так мы сразу увидим, совпадают ли диапа- зоны значений, и если нет, то насколько один ряд значений «выше» (S1), а вто- рой – «ниже» (S2). Для того, чтобы не запутаться, в этом и во многих других критериях рекомендуется первым рядом (выборкой, группой) считать тот ряд, где значения выше, а вторым рядом - тот, где значения ниже.

Гипотеза:Уровень признака в выборке 1 превышает уровень признака в выборке 2.

Графическое представление критерия Q

На Рисунке 7.23 представлены три варианта соотношения рядов значений в двух выборках. В варианте (а) все значения первого ряда выше всех значений второго ряда. Различия, безусловно, достоверны, при соблюдении условия, что n 1, n 2 <11.

1 См. Сидоренко Е. В. Методы математической обработки в психологии. СПб.: Соци- ально-психологический центр, 1996. – 349 с. – С. 42-48.

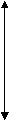
В варианте (б), напротив, оба ряда находятся на одном и том же уровне: различия недостоверны. В варианте (в) ряды частично перекрещиваются, но все же первый ряд оказывается гораздо выше второго. Достаточно ли велики зоны S1 и S2, в сумме составляющие Q, можно определить по таблице Приложение 6, где приведены критические значения Q для различных n. Чем величина Q больше, тем более достоверные различия мы сможем констатировать.

1 ряд

S1 2 ряд S2

а)

1 ряд

2 ряд S1=0 Z S2=0

б)

1 ряд Z

S1 2 ряд S2

в)

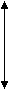Рисунок 7.23 - Возможные соотношения рядов значений в двух выборках

Примечание - S1 - зона значений 1-го ряда, которые выше максимального зна- чения 2-го ряда; S2 - зона значений второго ряда, которые меньше минималь- ного значения 1-го ряда; перекрещивающиеся зоны двух рядов отмечены бук- вой - Z

Ограничения критерия Q

1. В каждой из сопоставляемых выборок должно быть не менее 11 наблюдений. Условие: объемы выборок должны примерно совпадать.

При этом существуют следующие правила:

а) если в обеих выборках меньше 50 наблюдений, то абсолютная величи- на разности между n 1 и n 2 не должна быть больше 10 наблюдений;

б) если в каждой из выборок больше 51 наблюдения, но меньше 100, то абсолютная величина разности между n 1 и n 2 не должна быть больше 20 наблюдений;

в) если в каждой из выборок больше 100 наблюдений, то допускается, чтобы одна из выборок была больше другой не более чем в 1,5-2 раза.1

2. Диапазоны разброса значений в двух выборках должны не совпадать между собой, в противном случае применение критерия бессмысленно. Между тем, возможны случаи, когда диапазоны разброса значений совпадают, но, вследствие разносторонней асимметрии двух распределений, различия в сред- них величинах признаков существенны (Рисунок 7.24 и 7.25).

1) Гублер Е.В. Вычислительные методы анализа и распознавания патологических по- следствий. Л.: Медицина, 1978. – 296 с. - с. 75.

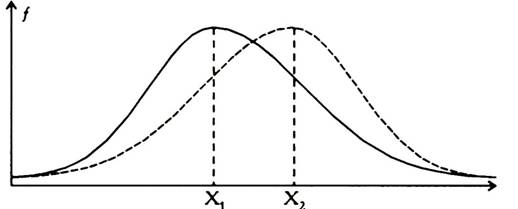
Рисунок 7.24. Вариант соотношения распределений признака в двух вы- борках, при котором критерий Q беспомощен

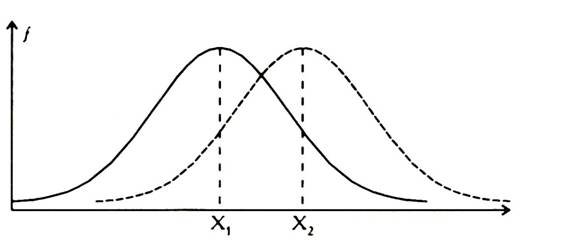
Рисунок 7.25. Вариант соотношения распределений признака в двух вы- борках, при котором используется критерий Q

Пример

У участников психологического эксперимента был измерен уровень вер- бального и невербального интеллекта с помощью методики Д. Векслера. Было обследовано 26 юношей в возрасте от 18 до 24 лет (средний возраст 20,5 лет). 14 из них были студентами физического факультета, а 12 - студентами психо- логического факультета Ленинградского университета (Сидоренко Е.В., 1978). Показатели вербального интеллекта представлены в Таблице 7.6.

Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта?

Таблица 7.6 - Индивидуальные значения вербального интеллекта в выборках студентов физического (n 1=14) и психологического (n 2 = 12) факультетов

Студенты-физики			Студенты - психологи
Код имени Показатель вербального испытуемого интеллекта		Код имени Показатель вербального испытуемого интеллекта
И. А	132	Н. Т.	126
К. А.	134	О. В.	127
К. Е.	124	Е. В.	132
П. А.	132	Ф. О.	120
С. А.	135	И. Н.	119
Ст. А.	132	И. Ч.	126
Т. А.	131	И. В.	120
Ф. А.	132	К. О.	123
Ч. И.	121	Р. Р.	120
Ц. А. См. А. К. Ан.	127 136 129	Р. И О. К Н. К.	116 123 115
Б. Л.	136
Ф. В.	136

Упорядочим значения в обеих выборках, а затем сформулируем гипотезу: Студенты-физики превосходят студентов-психологов по уровню вер-

бального интеллекта.

Таблица 7.7 - Упорядоченные по убыванию вербального интеллекта ряды ин- дивидуальных значений в двух студенческих выборках

1 – ряд студенты-физики			2 ряд – студенты психологи
1 См. А. 136			----------------------------------------------------------
2 Б. Л. 136
3 Ф. В. 136 S1
4 С. А. 135
5 К. А. 134
-------------------------------------------------------
6	И. А.	132	1	Е. В.	132
7 П. А. 132
8 Ст. А. 132
9 Ф. А. 132
10 Т. А. 131
11 К. Ан. 129
12	Ц. А.	127	2	О. В.	127
			3	Н. Т.	126
			4	И. Ч.	126
13 К. Е. 124
			5	К. О.	123
			6	О. К.	123
14 Ч.И. 121
----------------------------------------------------------			--------------------------------------------------------
			7	Ф. О.	120
			8	И. В.	120

9	Р. Р.	120	S2
10	И. Н.	119
11	Р. И.	116
12	Н. К.	115

Как видно из Таблицы 7.7, мы правильно обозначили ряды: первый, тот, что «выше» - ряд физиков, а второй, тот, что «ниже» - ряд психологов.

По Таблице 7.7 определяем количество значений первого ряда, которые больше максимального значения второго ряда: S1 = 5.

Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: S2 = 6.

Вычисляем Q эмп по формуле: Q эмп = S1 + S 2 = 5 + 6 = 11;

По Таблице 1 Приложения 6 определяем критические значения Q для n1

= 14, n 2 = 12:

Q кр =

7 (p ≤ 0,05)

9 (p ≤ 0,01)

Ясно, что чем больше расхождения между выборками, тем больше вели- чина Q. В данном случае Q эмп = 11, превышает Q кр = 9 (p ≤ 0,01) по табли- це.

На основании этого мы можем сделать вывод: студенты-физики превос- ходят студентов-психологов по уровню вербального интеллекта (р<0,01), т. е. гипотеза подтвердилась.

Поскольку уровень значимости выявленных различий достаточно высок (р<0,01), мы могли бы на этом остановиться. Однако если исследователь сам психолог, а не физик, вряд ли он на этом остановится. Он может попробовать сопоставить выборки по уровню невербального интеллекта, поскольку именно невербальный интеллект определяет уровень интеллекта в целом и степень его организованности.

Поэтому, потребуется еще ряд экспериментов (психологических обследо- ваний), чтобы окончательно ответить на вопрос о соотношении уровней интел- лекта в двух выборках. Быть может, психологи еще окажутся в более высоком ряду!

Алгоритм подсчета критерия Q Розенбаума

1. Проверить, выполняются ли ограничения: n1, n2 ≥ 11, n 1 ≈ n 2.

2. Упорядочить значения отдельно в каждой выборке по'степени возрас- тания признака. Считать выборкой 1 ту выборку, значения в которой предпо- ложительно выше, а выборкой 2 - ту, где значения предположительно ниже.

3. Определить самое высокое (максимальное) значение в выборке 2.

4. Подсчитать количество значений в выборке 1, которые выше макси- мального значения в выборке 2. Обозначить полученную величину как S1.

5. Определить самое низкое (минимальное) значение в выборке 1.

6. Подсчитать количество значений в выборке 2, которые ниже мини- мального значения выборки 1. Обозначить полученную величину как S2.

7. Подсчитать эмпирическое значение Q по формуле: Q = S1 + S2.

8. По Табл. _ Приложения _ определить критические значения Q, для данных n1 и n2. Если Q эмп равно Q 0,05 или превышает его, то подтверждается гипотеза (предположение) о существовании различий на достоверно значимом уровне.

9. При n1, n2 > 26 сопоставить полученное эмпирическое значение с Qкр = 8 (p ≤ 0,05) и Qкр = 10 (p ≤ 0,01). Если Qэмп превышает или по крайней мере равняется Qкр = 8 , то подтверждается гипотеза о существовании достоверных различий между исследуемыми выборками.

Критерий U Манна-Уитни 1

Назначение критерия

Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выяв- лять различия между малыми выборками, когда n1, n2 ≥3 или n1 = 2, n2 ≥ 5, и яв- ляется более мощным, чем критерий Q Розенбаума.

Описание критерия

Существует несколько способов использования критерия и несколько ва- риантов таблиц критических значений, соответствующих этим способам (Губ- лер Е. В., 1978; Рунион Р., 1982; Захаров В. П., 1985).

Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оцен- ке, выше, а 2-м рядом - тот, где они предположительно ниже.

Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в распо- ложении двух выборок. Эмпирическое значение критерия и отражает то,

1 См. Сидоренко Е. В. Методы математической обработки в психологии. СПб.: Соци- ально-психологический центр, 1996. – 349 с. – С. 49-55.

насколько велика зона совпадения между рядами. Поэтому чем меньше U эмп.,

тем более вероятно, что различия достоверны.

Гипотезы

Уровень не вербального интеллекта в группе студентов физиков выше, чем в группе студентов-психологов.

Графическое представление критерия U

На Рисунке 7.26 представлены три из множества возможных вариантов соотношения двух рядов значений.

В варианте (а) второй ряд ниже первого, и ряды почти не перекрещива- ются. Область наложения (S1)слишком мала, чтобы скрадывать различия между рядами. Есть шанс, что различия между ними достоверны. Точно определить это мы сможем с помощью критерия U.

В варианте (б) второй ряд тоже ниже первого, но и область перекрещи- вающихся значений у двух рядов достаточно обширна (S 2 ). Она может еще не достигать критической величины, когда различия придется признать несуще- ственными. Но так ли это, можно определить только путем точного подсчета критерия U.

В варианте (в) второй ряд ниже первого, но область наложения настолько обширна (S 3 ), что различия между рядами скрадываются.

1 ряд

2 ряд S1

а)

1 ряд

2 ряд S2

б)

1 ряд

2 ряд S3

в)

Рисунок 7.26 - Возможные варианты соотношений рядов значений в двух выборках.

Примечание - Перекрытием (S 1, S 2,, S 3 ) обозначены зоны возможного наложения.

Ограничения критерия U

1. В каждой выборке должно быть не менее 3 наблюдений: n1, n2 ≥ 3; допуска- ется, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.

2. В каждой выборке должно быть не более 60 наблюдений; n1, n2 ≤ 60. Однако уже при n1, n2 ≥ 20 ранжирование становиться достаточно трудоемким.

Пример

Вернемся к результатам обследования студентов физического и психоло- гического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. С помощью критерия Q Розенбаума в предыдущем разделе было с высоким уровнем значи- мости определено, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводит- ся ли этот результат при сопоставлении выборок по уровню невербального ин- теллекта. Данные приведены в Таблице 7.8.

Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?

Таблица 7.8 - Индивидуальные значения невербального интеллекта в выборках студентов физического (n = 14) и психологического (n = 12) факультетов

Студенты-физики			Студенты-психологи
Код имени испытуе- мого	Показатель невер- бального интеллекта		Код имени испытуе- мого	Показатель невер- бального интеллекта
1. И.А.		111	1. Н.Т.	113
2. КА.		104	2. О.В.	107
3. К.Е.		107	3. Е.В.	123
4. ПА.		90	4. Ф.О.	122
5. С.А.		115	5, И.Н.	117
6. СтА.		107	6. И.Ч.	112
7. ТА.		106	7. И.В.	105
8. ФА.		107	8. К.О.	108
9. Ч.И.		95	9. Р.Р.	111
10. ЦА. 11. СмА.		116 127	10. Р.И. 11. О.К.	114 102
12. КАн.		115	12. Н.К.	104
13. Б.Л.		102
14. Ф.В.		99

Критерий U требует тщательности и внимания. Прежде всего, необходи- мо помнить правила ранжирования.

Правила ранжирования

1. Меньшему значению начисляется меньший ранг. Наименьшему значе- нию начисляется ранг 1. Наибольшему значению начисляется ранг, соответ- ствующий количеству ранжируемых значений. Например, если n = 7, то наибольшее значение получит ранг 7, за возможным исключением для тех слу- чаев, которые предусмотрены правилом 2.

2. В случае, если несколько значений равны, им начисляется ранг, пред- ставляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Например, 3 наименьших значения равны 10 секундам. Если бы мы изме- ряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, со- ответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:

1 + 2 + 3 = 6 = 2

3 3

Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:

4 + 5 = 4,5

и т.д.

3. Общая сумма рангов должна совпадать с расчетной, которая определя- ется по формуле:

Σ (Ri) ═

N ´ (N + 1) ; 2

(7.6)

где N - общее количество ранжируемых наблюдений (значений).

Несовпадение реальной и расчетной сумм рангов будет свидетельство- вать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

При подсчете критерия U лучше всего действовать по строгому алгорит-

му.

Алгоритм подсчета критерия U Манна-Уитни

1. Перенести все данные испытуемых на индивидуальные карточки.

2. Пометить карточки испытуемых выборки 1 одним цветом, скажем

красным, а все карточки из выборки 2 - другим, например, синим.

3. Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.

4. Проранжировать значения на карточках, приписывая меньшему значе- нию меньший ранг. Всего рангов получится столько, сколько у нас (n1 + n2).

5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой.

6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.

7. Определить большую из двух ранговых сумм.

8. Определить значение U по формуле:

nx ´ (nx

U =(n1 + n2) + 2

+ 1)

- Tx (7.7)

где n1 - количество испытуемых в выборке 1; n2 - количество испытуемых в выборке 2; Tx - большая из двух ранговых сумм;

nx - количество испытуемых в группе с большей суммой рангов.

9. Определить критические значения U по Таблице см. Приложение 7. Если U эмп < U кр 0,05, то принимается гипотеза о том, что уровень признака в выборке 2 ниже уровня признака в выборке 1 на достоверно значимом уровне. Чем меньше значения U, тем достоверность различий выше.

Теперь проделаем всю эту работу на материале данного примера. В ре- зультате работы по 1-6 шагам алгоритма построим таблицу (Таблица 7.27).

Таблица 7.27 - Подсчет ранговых сумм по выборкам студентов физического и психологического факультетов

Студенты-физики (n = 14)		Студенты-психологи (n = 12)
Показатель не- интеллекта	Ранг	Показатель не- интеллекта	Ранг
127	26	123	25
		123	25
		122	24
		117	23
116	22
115	20,5
115	20,5
		114	19
		113	18
		112	17
111	15,5	111	15.5
		108	14
107	11.5	107	11,5
107	11,5
107	11,5
106	9
		105	8
104	6,5	104	6,5
102	4,5	102	4,5
99	3
95	2
90	1
Суммы 1501	165	1338	186
Средние 107,2		111,5

Общая сумма рангов: 165 + 186 = 351. Расчетная сумма:

N ´ (N + 1)

∑ Ri = 2

=26 ´ (26 + 1)

= 351

Равенство реальной и расчетной сумм соблюдено. Мы видим, что по уровню невербального интеллекта более «высоким» рядом оказывается выбор- ка студентов-психологов. Именно на эту выборку приходится большая ранговая сумма: 186. Теперь мы готовы сформулировать статистические гипотезы:

Н0: Группа студентов-психологов не превосходит группу студентов- физиков по уровню невербального интеллекта.

Н1 Группа студентов-психологов превосходит группу студентов-физиков по уровню невербального интеллекта.

В соответствии со следующим шагом алгоритма определяем эмпириче- скую величину U:

12 ´ (12 + 1)

U эмп = (14 + 12) + 2

- 186 = 60

Поскольку в нашем случае n1 ≠ n2 подсчитаем эмпирическую величину U и для второй ранговой суммы (165), подставляя в формулу соответствующее ей nx:

U эмп = (14 + 12) + 14 ´ (14 + 1)

- 165 = 108

Такую проверку рекомендуется производить в некоторых руководствах (Рунион Р., 1982 и др.). Для сопоставления с критическим значением выбираем меньшую величину U: Uэмп = 60.

По Таблице

Приложения 7 определяем критические значения для

n1 = 14, n2 = 12:

U кр =

51 (p ≤ 0,05)

38 (p ≤ 0,01)

Мы помним, что критерий U является одним из двух исключений из об- щего правила принятия решения о достоверности различий, а именно, мы мо- жем констатировать достоверные различия если U эмп < U кр 0,05.

U эмп = 60

U эмп > U кр 0,05

Следовательно, Н0 принимается. Группа студентов-психологов не пре- восходит группы студентов-физиков по уровню невербального интеллекта.

Обратим внимание на то, что для данного случая Q-критерий Розенбаума неприменим, так как размах вариативности в группе физиков шире, чем в груп- пе психологов: и самое высокое, и самое низкое значение невербального интел- лекта приходится на группу физиков (см. Таблицу 7.27).

Ранговая корреляция

Среди непараметрических методов для выявления взаимосвязи суще- ствуют весьма несложные методы ранговой корреляции. Если обе переменные, между которыми изучается связь, представлены в порядковой шкале, или одна из них - в порядковой, а другая - в метрической, то можно использовать ранго- вый коэффициент корреляции r-Спирмена особенно для небольших выборок. Вычисление коэффициента достаточно просто, но требует для своего примене- ния предварительного ранжирования обеих переменных.

Коэффициент корреляции r-Спирмена1

Если члены группы численностью N были ранжированы сначала по пере- менной X, затем — по переменной Y, то корреляцию между переменными Х и Y можно получить, просто вычислив коэффициент r-Пирсона для двух рядов ран- гов. При условии отсутствия связей в рангах (т. е. отсутствия повторяющихся рангов) по той и другой переменной, формула для r-Пирсона может быть суще- ственно упрощена в вычислительном отношении и преобразована в формулу, известную как r-Спирмена:

6åd 2

rS = 1 -

N ´ (N 2 - 1) ; (7.8)

где dI , — разность рангов для испытуемого с номером i.

N –численность выборки (членов группы).

Коэффициент корреляции r-Спирмена (Spearman,s rho) равен коэффици- енту корреляции r-Пирсона, вычисленному для двух предварительно ранжиро- ванных переменных.

Пример:

Предположим, для каждого из 12 учащихся одного класса известно время решения тестовой арифметической задачи в секундах (X) и средний балл отме- ток по математике за последнюю четверть (Y). Данные приведены в Таблице 7.28.

1 Наследов А. Д. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. – СПб.: Речь, 2004. – 392 с. – C.77 – 78.

Таблица 7.28

№	X	У	Ранги X	Ранги У	di	di2
1	122	4,7	7	1	5	25
2	105	4,5	10	4	6	36
3	100	4,4	11	5	6	36
4	145	3,8	5	9	-4	16
5	130	3,7	6	10	-4	16
6	90	4,6	12	3	9	81
7	162	4,0	3	8	-5	25
8	172	4,2	1	6	-5	25
9	120	4,1	8	7	1	1
10	150	3,6	4	11	-7	49
11	170	3,5	2	12	-10	100
12	112	4,8	9	1	8	64
Σ	-	-	78	78	0	474

Для расчета корреляции r-Спирмена сначала необходимо ранжировать учащих- ся по той и другой переменной. После ранжирования можно проверить его пра- вильность: сумма рангов должна быть равна N(N+ 1 )/2. Затем для каждого ис- пытуемого надо вычислить разность рангов (di). Сумма разностей рангов долж- на быть равна 0. После этого для каждого испытуемого вычисляется квадрат разности рангов - результат приведен в последнем столбце таблицы (di2). Сум- ма квадратов разностей рангов равна 474.

Подставляем известные значения в выше приведенную формулу (7.8):

rS = 1 -

6 ´ 474

12 ´ (144 - 1)

= - 0,657

Сравниваем с табличным значением Приложение 5 для n = 12, получена умеренная отрицательная связь (p<0,05) между успеваемостью по математике и временем решения арифметической задачи.

Отметим: то же значение корреляции было бы получено при использова- нии формулы r-Пирсона непосредственно к рангам Х и Y. Применяя же форму- лу r-Пирсона к исходным значениям Х и Y, мы получим rxy = - 0,692.

Дата добавления: 2018-06-01; просмотров: 348; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!