Топологія розшаровувань Ліувілля інтегровного випадку Матвєєва-Дулліна

4.1. Інтегровний випадок.В роботі [12] знайдений новий інтегрований випадок на одній з орбіт коприєднаної дії групи E (3), а саме на різноманітті M ⁴ = {x² + y² + z² = 1, xL_x + yL_y + zL_z = 0} в координатах, описаних вище. Покладемо A, c, s ∈ R, де параметри s > 1, A > 0. Визначимо функції

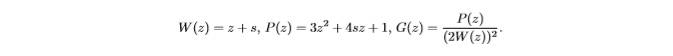
Тоді гамільтоніан запишеться у вигляді:

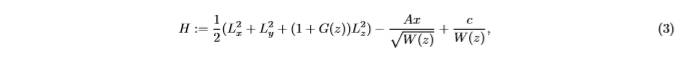
А додатковий перший інтеграл:

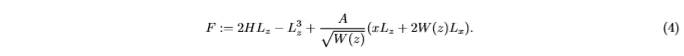
Слід особливо відзначити, що дана система має інтеграл третього ступеня по імпульсам так само як і класичний випадок Горячева-Чаплигіна. Згідно [11], цей випадок разом з випадком Горячева-Чаплигіна

1,0

 належить чотирьохпараметричній сім’ї інтегровних випадків на M ⁴ з інтегралом третьої степені за імпульсами.

 

4.2. Топологія ізоенергетичних поверхнонь.Для пошуку критичних точок векторного поля існують ті ж самі два способи, що і при пошуку критичних точок відображення моменту. Або знаходимо точки, в яких залежні градієнти функцій I₁, I₂ і H як фунуції осяжного шестимірного простору

c1,c2

, потім обмежуємо цю множину на M ⁴. Або вважаємо вектор косого градієнта H як показано вище,прирівнюємо всі його компоненти до нуля і  знову  ж      обмежуємо  отриману множину точок М

.

c₁,c₂

Функція на многовиді називається функцією Морса або морсовской функцією, якщо всі її критичні точки невирождені в тому сенсі, що в цих точках невирождені матриці других похідних. Таке визначення цілком коректне. Ну дійсно, гессіан функції в критичній точці, як це добре відомо, є тензором типу (0, 2), а тому умова його невиродженості не залежить від вибору координат на многовиді. Основна теорема теорії функцій Морса.

ТЕОРЕМА 3 (Лема Морса). Нехай x₀ — критична точка функції Морса f на многовиді M ⁿ. Тоді існують такі локальні кооррдинати (x¹, x², ..., xⁿ) в околі точки x₀, що функція   f  прийме вигляд:для деякого цілого k від 0 до n.

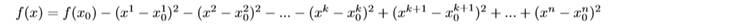
Число k, очевидним чином, для кожної критичної точки визначене однозначно - воно визначається сигнатурою матриці гессіана функції. При цьому таку точку будемо називати сідловою типу (k, n - k).

Повернемося до інтегровних випадків.

 

1,0

ТЕОРЕМА 4. Множину критичних точок гамільтоніана випадку Матвєєва-Дулліна    на M ⁴

Можна представити у вигляді:

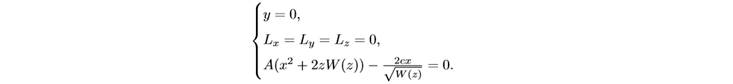
У разі c = 0 система сильно спрощується, і тому можна додати, що при c = 0

• Інтеграл енергії Н на 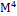 має тільки два критичних значення:

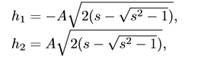
• Критичні точки ξ₁ и ξ₂, що відповідають критичним значенням h₁ и h₂, обидві невирождені, тобто інтеграл энергії H на M ⁴ є функцією Морса.

• Критичніточки ξ₁ и ξ₂ єточками рангу нуль відображення моменту.

• Критична точка, що відповідає значеню h₁, — точка глобального мінімуму.

• Критична точка, що відповідає значеню h₂, — сідлова точка типу (2, 2).

• Неособі ізоенергетичні поверхні мать наступний топологічний тип:

h

∀h ∈ (−∞, h₁) Q³ = ∅,

h

∀h ∈ (h₁, h₂) Q³ ∼= S³,

h

∀h ∈ (h₂, ∞) Q³ ∼= RP ³.

---

Дата добавления: 2018-06-01; просмотров: 382; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!