Топологічна класифікація інтегровних гамільтонових систем з двома ступенями свободи.
Nbsp; МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ “КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ ІМ. І. СІКОРСЬКОГО” Фізико-математичний факультет
Кафедра диференціальних рівнянь
Курсова робота
з дисципліни «Диференціальні рівняння»
«Топологія розшарування Ліувілля
інтегрувального випадку Матвєєва-Дулліна»
Виконав: студент гр. ОМ-61
Кононенко С.В.
Затвердив: Пелюх Г. П.
Київ 2018
Вступ
У роботах [1], [2], [3] А.Т. Фоменко, Х. Цішангом, А.В. Болсіновим, А.А. Ошемкова була розвинена теорія про топологічної класифікації інтегрованих випадків з двома ступенями свободи. Був побудований інварі- ант, який допомагає класифікувати інтегровані випадки з двома ступенями свободи з точністю до ліуіллевой еквівалентності. В [12] В.С. Матвєєвим і Х.Р. Дулліним знайдений новий інтегрований випадок.
У даній роботі для випадку Матвєєва-Дулліна знайдено безліч критичних точок і безліч критичних значень відображення моменту, топологія ізоенергетичних поверхонь, особливі точки векторного поля і їх тип, кількість критичних кіл в прообраз кривих бифуркационной діаграми. На компью- тере пораховані індекси критичних кіл, і зроблено висновок про тип грубих молекулах інтегрувального випадку.
|
|
|
Інтегрувальні системи Гамільтона на симплектичних многовидах
2.1. Основні поняття в Симплектичній геометрії . Ознайомитися з доказами тверджень з цього розділу можна в будь-якій книзі по сімплектичній геометрії. Припустимо в [8].
ВИЗНАЧЕННЯ 1. дужки Пуассона на многовиді M n називається відображення{·, ·} : C∞(M n) ×
C∞(M n) → C∞(M n) з властивостями:
1) {λf + µg, h} = λ{f, h} + µ{g, h}, λ, µ ∈ R — лінійність ,
2) {f, g} = −{g, f } — кососиметричність,
3) {f, {g, h}} + {g, {h, f }} + {h, {f, g}} = 0 — тотожність Якобі.
Многовид, який має дужку Пуассона, будемо називати пуассоновим.
Таким чином, всі гладкі функції на пуассоновому многовиді зі структурою дужки утворюють алгебру Лі. Дужка Пуассона щодо кожної з змінних є оператором диференціювання в пропросторі функцій C∞(Mn). Тому в локальних координатах вона приймає спрощений вигляд:
ТВЕРДЖЕННЯ 1. У будь-яких локальних координатах(x1, x2, ..., xn) дужка Пуассона-Лі може бути записана у вигляді:
Неважко перевірити, функції πij = {xi, xj}, визначаються в локальних координатах на многовиді утворюють кососиметричний тензор типу (2, 0). Цей тензор називається тензором Пуассона. І, фактично, визначити дужку Пуассона означає визначити тензор Пуассона. Тільки слід розуміти, що не всякий кососімметріческіх тензор типу (2, 0) може бути тензором Пуассона деякої дужки. Цьому перешкоджає тотожність Якобі. Кососиметричний тензор типу (2, 0) на многовиді є тензором Пуассона деякої дужки тоді і тільки тоді,коли
|
|
|
ВИЗНАЧЕННЯ 2. Симплектичною структурою на гладкому многовиді M називається диференціальна
2-форма ω, що задовольняє двом умовам :
1) ω замкнута, тобто dω = 0
2) ω не вироджена в кожній точці многовиду, тобто в будь-яких локальных координатах detΩ(x) 
0, где
Ω(x) = (ωij(x)) — матриця форми.
Многовид, оснащений симплектичною структурою, називаєтся симплектичним.
Очевидно, що при таких обмеженнях симплектичний многовид може бути лише парномірним. Коефіцієнт матриці 2-форми ω утворює кососимметричний тензор типу (0, 2) з двома нижніми індексами. Оскільки симплектична форма невирождена, її можна звернути і отримати кососімметричний тензор типу (2, 0) вже з двома верхніми індексами 
ij. Отже, на симплектичному многовиді можна ввести дужку наступним чином:
|
|
|
Нескладно показати, що умова замкнутості сімплектичної форми в точності збігається з умовою (1).Таким чином, будь-який симплектичний многообраз є пуассонівським. Прикладом пуассонівського многовиду може служити будь-яка коалгебра алгебри Лі. Если (x1, x2, ..., xn) —
|
|
|
|
Тензор Пуассона коалгебри буде: 
. Взагалі кажучи, тензор Пуассона повинен мати два верхніх індексу, але в коалгебрі прийнято координатні функції писати з нижніми індексами, тому і вийшов тензор з двома нижніми індексами.
Передбачається, що читач знайомий з основними поняттями алгебри Лі. Хоча б з такими, як приєднана, коприєднана дія групи, орбіти дії, форма Кирилова. Вище було наведено класичний приклад пуассоівського многовиду. Наступне твердження допомагає ввести деякий корисний для додатків клас симплектичних многовидів.
орбиты действия, форма Кириллова. Выше был приведен класси- ческий пример пуассонова многообразия. Следующее утверждение помогает ввести некоторый полезный для приложений класс симплектических многообразий.
|
|
|
ТВЕРДЖЕННЯ 2. Орбіти коприєднаної дії групи Лі на своїй коалгебрі G* всі є симплектичними многовидами з канонічною 2-формою ω - формою Кирилова. Форма Кирилова є обмеженням тензора Пуассона коалгебри на орбіту. Дужку Пуассона на цих многовидах можна вважати таким чином: если f, g — дві гладкі функції на орбіті, продовжуємо їх довільним чином до гладких функцій f˜, g˜ на всій коалгебрі, тоді {f, g}(x) = {f˜, g˜}(x)
Тензор Пуассона πij є тензором з верхніми індексами, а для тензорів з верхніми індексами, взагалі кажучи, немає природного визначення обмеження з різноманіття на підмноговидів. На відміну від тензорів з нижніми індексами. Але в разі пуассонівських многовидів є загальний метод, який все ж дозволяє провести обмеження тензора Пуассона на симплектичні шари цього пуассонівського многовиду. У нашому випадку - на орбіти. Причому це обмеження є невироджених кососімметріческіх тензором ωij типу (2, 0) вже на орбіті, а 2-форма, задана матрицею ωij, є замкнутою. Сам метод обмеження тензора Пуассона на орбіту описаний в [5]. Надалі в цій роботі знадобиться лише знання про те, як влаштована дужка Пуассона на орбітах. Причому твердження 2 цілком достатньо, тобто сам метод обмеження тензора Пуассона з коалгебри на орбіту не буде потрібно.
2.2. Коалгебра Ліe(3)∗.Застосуємо всі введені вище конструкції до коалгебри Лі e(3)∗ групи рухів тривимірного простору. Це шестімерна коалгебра. У ній можна ввести вже стандартні координати Lx, Ly, Lz, x, y, z, в яких тензор Пуассона виглядатиме так:
Змінні Lx,Ly,Lz принято називати імпульсами. По тензору Пуассона можна зрозуміти, як влаштована дужка Пуассона на цій коалгебрі. На коалгебрі e(3)∗ є дві функції Казимира, тобто функції, комутуючі відносно дужки з усіма гладкими функціями на коалгебрі. Это I1 = x2 + y2 + z2 — її прийнято називати геометричним інтегралом, і I2 = xLx + yLy + zLz — інтеграл площ. А також для коалгебри e(3)∗ справедливе наступне твердження, що показує, як вона розшаровується на симплектичні многовиди.
|
= {I1 = c1, I2 = c2} — орбІта коприєднаної дії групи.
|
ні кодотичному розшаруванню до двувимірної сфери T ∗S2.
2.3 Інтегровність за Ліувіллем.Розглянемо динамічні рівняння на пуассоновых многовидах.
ОЗНАЧЕННЯ 3. Векторне поле v на многовиді M n, оснащеному структурою дужки Пуассона, називається гамільтоновмм з гамильтоніаном H ∈ C∞(M n), якщо для будь-якого f ∈ C∞(M n) : {f, H} = v(f ). В такому випадку пишуть v = sgrad H.
Або в локальных координатах
vi = πij ∂H
∂xj
= {xi, H}.
Гамільтонова динамічна система на многовиді, оснащеному пуассоновою структурою, має вигляд x˙ = sgrad H. Або в локальных координатах x˙i = {xi, H}, i = 1, 2, .., n. Для інтегралів гамільтонових векторних полів вірно наступне: F є інтегралом гамільтонового векторного поля з гамильтоніаном H тоді і тільки тоді, коли {F, H} = 0. В такому випадку гамільтоніан гамільтонового векторного поля завжди є інтегралом цього поля. При цьому дужка двох інтегралів знову буде інтегралом. Дійсно , з тотожності Якобі {{G, F }, H} = {F, {H, G}} + {G, {F, H}} = 0. Таким чином, безліч інтегралів гамільтонового векторного поля є підалгеброю алгебри Лі гладких функцій. Ця підалгебра є максимальною, тобто непоповнювана, і визначається одні гамильтоніаном. Перейдемо до розгляду симплектичних многовидів і гамільтонових векторних полів на них.
ОЗНАЧЕННЯ 4. Гамільтонова система v на симплектичному многовиді M 2n называється цілком інтегровною за Ліувіллем, якщо існує набір гладких функцій f1, f2, ..., fn таких, що:
1) f1, f2, ..., fn — перші інтеграли v,
2) вони функціонально незалежні на M 2n, тобто майже всюди на M 2n градієнти лінійно-незалежні,
3) {fi, fj} = 0 для будь-яких i и j,
4) векторніе поля повні, тобто природні параметри на їхніх інтегральних траекторіях визначений на всій числовій прямій.
Виявляється, якщо на симплектичнму многовиді M 2nє цілком інтегрована гамільтонова система, то в "компактному" випадку це симплектична різноманіття може бути розшароване на n-мірні тори і особливі шари. Про це говорить нам наступна теорема:
ТЕОРЕМА 1(теормема Ліувіля): Нехай на симплектична різноманітті (M2n, ω) задана цілком інтегрована по Ліувілльюгамільтонова система v = sgradH и Tξ = {x ∈ M|fi(x) = ξi,i = 1,2,...,n} регулярна неособо поверхню рівня інтегралів f1,f2,...,fn. Тоді:
1) Якщо многовид Tξ звязний і компактний, то Tξ диффеоморфне n-іерному тору Tn. Цей тор называется тором Ліувілля.
2)Розшарування Ліувіля в деякому околі U тора Ліувілля Tξ тривиальне, тобто диффеоморфне прямому добутку тора T n на диск Dn.
|
разділу 2.2. При розгляді гамільтонової системи з двома ступенями свободи, тобто при n = 2,для інтегрованості по Ліувілль досить існування ще одного додаткового, що не залежить від га- мільтоніана, інтеграла.
Рівняння Ейлера руху твердого тіла із закріпленою точкою в полі сили тяжіння можуть бути записані в гамільтонових вигляді на симплектичних многовидах виді M4 c1,c2,c1 > 0. Як відомо з класичної механіки, в задачі про рух твердого тіла із закріпленою точкою фазовий простір шестімерной. З огляду на те, що таке завдання завжди має два інтеграла - геометричний і інтеграл площ - фазовий простір може бути редуцировано до чотиривимірного. Більш детально процес зведення задачі від шестімерной до чотиривимірної можна прочитати в [3, том 2, глава 5]. Відомо, що завдання про рух твердого тіла із закріпленою точкою в центрі мас і з різними моментами інерції, що відповідає відомому з класичної механіки нагоди Ейлера (1750 рік), може бути записана в гамільтонових вигляді на симплектичному многоовиді 
де g є R.Гамільтоніан при цьому буде мати вигляд:
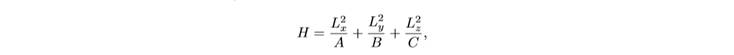
где A, B, C ∈ R всі позитивні і попарно різні. У разі Ейлера є додатковий інтеграл F = L2 + L2 + L2. Функції H і F коммутируют відносно дужки Пуассона на е(3)*
ВипадокЛагранжа (1788 год) Рух осесимметричного твердого тіла в полі сили тяжіння з
точкою кріплення на осі симетрії.
|
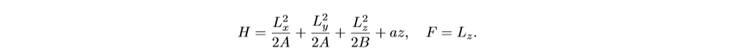
Тут інтеграл F - четвертого ступеня по імпульсам. В цьому випадку моменти інерції тіла A1, A2, A3 задовільняють умові A1 = A2 = 2A3, і центр мас тіла розташований в площині симетрії тіла, що відповідає першим двом осях інерції тіла.
Топологічна класифікація інтегровних гамільтонових систем з двома ступенями свободи.
3.1. Ліувіллева еквівалентність.В теорії топологічної класифікації інтегрованих гамільтоно- вих систем традиційно розглядаються кілька типів їх ізоморфізмів.
ВИЗНАЧЕННЯ 5. Дві інтегровані Гамільтона системи з двома ступенями свободи (M 4, v1) и (M 4, v2)
((Q3 1,v1) и (Q3 2,v2)) Ліувіллево еквівалентні якщо існує дифеоморфізм 
ОЗНАЧЕННЯ 6. Дві інтегруючі Гамільтонові системи (M 4, v1) и (M 4, v2) ((Q3, v1) и (Q3, v2)) нази-
1 2 1 2
ваються грубо ліувіллево еквівалентні, якщо існує гомеоморфізм між базами відповідних шарів Ліувілля, який локально (тобто в околиці кожної точки бази) піднімається до пошарового гомеоморфізма шарів Ліувілля.
3.2.
|
|
|
3.3.Оскільки гамильтониан є інтегралом гамільтонового векторного поля, вектор косого градієнта v = sgrad H спрямований уздовж ізоенергетичних поверхні. У інтегрувальному випадку на ізоенергетичних поверхнях можна розглянути потік косого градієнта додаткового інтеграла w = sgrad F. це векторне
|
|
|
Таким чином можна розглядати два векторних поля, а саме v = sgrad H і w = sgrad F. Причому, по-перше, перше векторне поле ніде на Q3 не звертається до нуль, по-друге, критичних точках відображення моменту будуть відповідати ті точки, де залежні векторні поля v і w, тобто w = λv. Відображенням моменту називається відображення H × F : M 4 → R2(h, f). Для топологического исследования интегрируемого случая с двумя степенями свободы полезно следующее утверждение:
ТВЕРДЖЕННЯ 4 [3, том 1, глава 1]. нтеграл F не може мати ізольованих критичних точок
на неособливій Q3 . У випадку компактної Q3 критичні точки F организовані в критичні кола.
h h
Кожне критичне коло проектується в одну точку на біфуркаційній діаграмі.Параметр λ
пропорціональності sgrad F і sgrad H постійний вздовж критичного кола.
|
Для кожної невиродженої критичної окружності відображення моменту можна ввести поняття індексу. Візьмемо точку на критичній окружності, і розглянемо сигнатуру квадратичної форми додаткового інтеграла F як функції на ізоенергетичних поверхні. Ця сигнатура не залежить від вибору точки на колі і може приймати одне з наступних трьох значень: (1, 1, 0), (1, -1, 0) або (-1, -1, 0). Як вже було відмічено, квадратична форма F виродилися. Індексом невироджених критичної окружності на- ни опиняються кількість негативних власних значень квадратичної форми d2F .
3.4. Біфуркації торів Ліувілля.Ізоенергетична поверхня Q3 являє собою однопараметричну сім’ю спільних поверхонь рівня Tξ інтегралів системи H і F, параметризрвані значенням другого інтеграла F. Якщо стягнути кожну компоненту зв'язності в точку, то ми отримаємо деякий однопараметричний граф - базу шарування Ліувілля (див. Рис. 1). Причому вершинам графа відповідатимуть критичні шари шарування.
 |
Рисунок 1.
Прообразом кожного відкритого ребра графа є многовид, диффеоморфний T 2 × (0, 1). Вершинам графа відповідають сингулярні шари. Типовою є ситуація, коли при переході через критичний рівень число компонент зв'язності Tξ змінюється.
Будемо розглядати тривимірний окіл особливого шару в Q3. Виявляється, що в боттівському випадку з точністю до ліувіллевой еквівалентності існує лише кінцеве число можливих перебудов (біфуркацій), якщо фіксувати кількість критичних кіл на сингулярному шарі.
ОЗНАЧЕННЯ 8. Клас ліувіллевой еквівалентності околиці особливого шару шарування Ліувілля називається 3-атомом.
По суті, 3-атом - це тривимірний многовид зі структурою ліувіллевого шарування, що містить рівно один сингулярний шар. Край такого різноманіття складається з деякого числа торів Ліувілля. Кількість критичних кіл на сингулярному шарі атома називається складністю 3-атома. В [3] викладено алго- ритм, що дозволяє явно перерахувати всі атоми заданої складності. Прийнято 3-атоми позначати великими латинськими літерами з натуральними індексами і зірочками. Три найбільш простих і найбільш типових 3-атома (A, A * і B) зображені на Рис. 2.
Рисунок 2
Якщо тепер в вершинах графа на Рис.1 поставити відповідний 3-атом, то ми отримаємо так звану грубу молекулу. Груба молекула несе інформацію про базу шарування Ліувілля, а також дозволяє локально відновити його структуру поблизу як регулярних, так і сингулярного шарів. Справедлива
ТЕОРЕМА 2 (А.Т. Фоменко [3]) Дві інтегровні гамільтонові системи (Q3, V1) и (Q3, V2) з ботівськими
1 2
Додатковими інтегралами F1 и F2 грубо ліувіллево еквівалентні в тому і тільки тому випадку, коли їх грубі молекули збігаються
Повний і послідовне доказ фактів, викладених в цьому пункті, можна знайти в [3].
3.5. Біфуркаційна діаграма відображення моменту.Розглянемо біфуркаційну діаграму на площині R2(h, f) деякої інтегрованої по Ліувілль системи. Біфуркаційних діаграма розбиває площину на кілька камер. У прообраз кожної точки камери лежить кілька торів Ліувілля, якщо у точки, звичайно ж, є прообрази. Для точок бифуркационной діаграми, що відповідає критичним точ- кам відображення моменту, в прообраз лежать сингулярні шари. Під рангом відображення моменту в точці прийнято розуміти ранг диференціала відображення моменту в цій точці.
|
Знаходимо точки, в яких залежні градієнти функцій I1, I2, H і F як функцій в e(3)∗. Потім отриману
|
|
значень відображення - це просто образ множини критичних точок при цьому відображенні.
Другий спосіб пошуку критичних точок відображення моменту може здатися схожим на перший, але іноді цей спосіб буває простіше здійснити. А саме, ми шукаємо вектора косих градієнтів інтегралів H
|
sgrad H = ({Lx, H}, {Ly, H}, {Lz, H}, {x, H}, {y, H}, {z, H}). Аналогічний вираз отримуємо для
sgrad F . Тепер знову ж дивимося точки, в яких залежні sgrad H і sgrad F в осяжному просторі,
|
моменту.
Дата добавления: 2018-06-01; просмотров: 333; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!