Анализ числовых характеристик последовательностей по результатам измерений
Найдем математическое ожидание и дисперсию по каждой координате.
 , (3.1)
, (3.1)
 (3.2)
(3.2)
где xi - i-ое значение случайной величины, n – количество значений случайной величины.
Расчеты представлены на рис. 21.

Рисунок 21. Обработка данных «diplom.csv»
Анализируя эти данные, можно заметить, что дисперсия последовательности по координате Yнамного выше других, это говорит о случайности данной последовательности.
Анализ статистических свойств двоичных последовательностей, полученных путем квантования данных магнитометра по критериям НИСТ
Математические основы оценивания случайной последовательности
Для получения двоичных последовательностей, обработаем уже имеющиеся. От каждого значения трех последовательностей вычтем соответствующее им математическое ожидание и получим три центрированных последовательности (A, B, C). После этого проведем квантование первой последовательности А: если Ai≥0, то в свободную ячейку запишем 1, еслиAi<0, то запишем 0,и так для каждой из последовательностей. После получения трех двоичных последовательностей, найдем математическое ожидание и дисперсию. Видим, что для последовательности  математическое ожидание по результатам измерений наиболее близко к теоретическому значению 0.5 (рис.22). Это же справедливо и для дисперсии (для равновероятной последовательности Dx=0.25).
математическое ожидание по результатам измерений наиболее близко к теоретическому значению 0.5 (рис.22). Это же справедливо и для дисперсии (для равновероятной последовательности Dx=0.25).
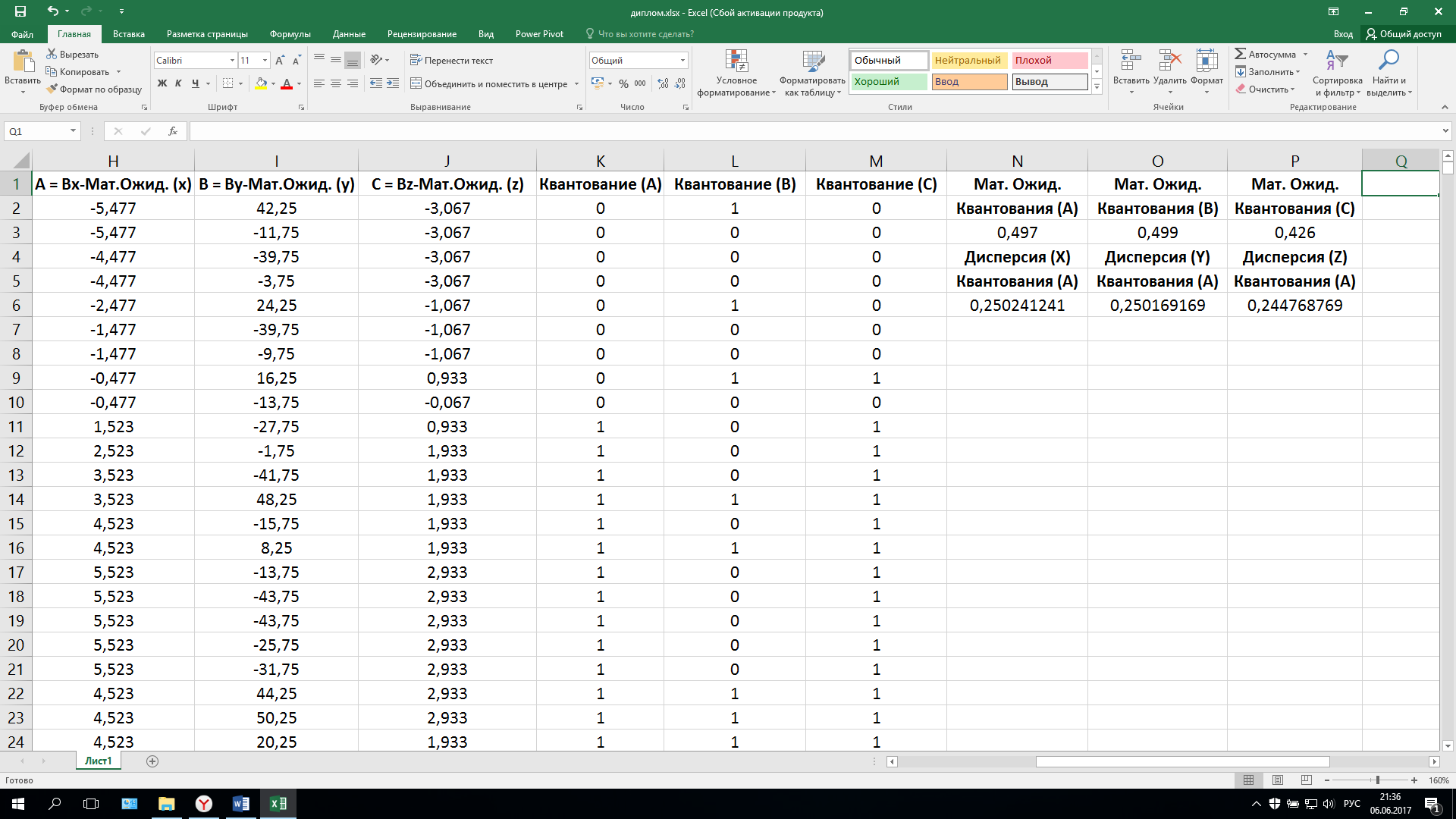
Рисунок 22. Обработка и анализ данных «diplom.csv»
Таким образом можно сделать вывод, что лучшими статическими характеристиками обладает последовательность  , а квантованные последовательности
, а квантованные последовательности 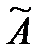 и
и  имеют большие серии повторения значений. Поэтому далее мы будем работать исключительно с последовательностью B.
имеют большие серии повторения значений. Поэтому далее мы будем работать исключительно с последовательностью B.
Для более детальной оценки статических характеристик этой последовательности рассмотрим сначала математические основы оценивания случайной последовательности. Свойства случайности либо псевдослучайной последовательности могут быть охарактеризованы и описаны в вероятностном виде. Существует множество тестов, которые дают оценку, является ли последовательность случайной.
Статистический тест формулируется для проверки определенной нулевой гипотезыH0о том, что последовательность – случайна. С этой нулевой гипотезой связана альтернативная гипотезаHA, что последовательность не является случайной. Для каждого применяемого теста можно сделать вывод касательно принятия либо отклонения нулевой гипотезы, исходя из сформированной генератором последовательности.
Для каждого теста следует выбрать адекватную статистику случайности, на основании которой может быть принята либо отклонена нулевая гипотеза. Соответственно о допущении на случайность, такая статистика обладает некоторым распределением случайных значением. Теоретически для нулевой гипотезы распределение этой статистики определяется математическими методами. Из этого эталонного распределения определяется критическое значение. Во время проведения теста рассчитывается значение тестовой статистики. Это значение сравнивается с критическим значением. Если критическое значение тестовой статистики превышает критическое значение, нулевая гипотеза касательно случайности отклоняется. Иначе нулевая гипотеза принимается.
Проверка статистических гипотез работает благодаря тому, что эталонное распределение и критические значения зависят и генерируются в соответствии с допущением о случайности. Если допущение о случайности – истинно, то результат тестовой статистики для нее будет иметь очень низкую вероятность превышения критического значения (например: 0,01). Если расчетное значение тестовой статистики превышает критическое значение (тоесть возникает событие с очень низкой вероятностью), тогда с точки зрения проверки статистической гипотезы событие с низкой вероятностью не может встречаться по своей природе. В связи с этим, когда расчетное значение тестовой статистики превышает критическое значение, делается вывод, что первое допущение касательно случайности является подозрительным либо ошибочным. В таком случае делается вывод об отклоненииH0(случайность), и принятии HA(не случайность). Проверка статистической гипотезы является процедурой генерации выводов, во время выполнения которой можно либо принятьH0(данные случайные) либо отклонить H0(данные не случайные). Таблица 1 связывает истинное (неизвестное) состояние данных с выводом, полученным посредством процедуры проверки.
Таблица 1. Принятие заключений по результатам проведения статистических испытаний
| Ситуация | Заключение | |
| ПринятьH0 | Принять HA | |
| Данные случайны (H0истина) | Нет ошибки | Ошибка 1-го рода |
| Данные не случайны (HA истина) | Ошибка 2-го рода | Нет ошибки |
.
Если данные действительно случайные, то вывод об отклонении нулевой гипотезы принимается очень редко, этот вывод имеет название «Ошибка первого рода». Если данные не случайные, то вывод о принятии нулевой гипотезы (то есть данные случайные) имеет название «Ошибка второго рода». Вывод о принятии H0, когда данные действительно случайные, и отклонение H0, когда данные не случайные является правильным.
Вероятность ошибка 1-го рода называется уровнем значимости теста. Эта вероятность может быть установлена для тестов и обозначается как a . Для теста суть a состоит в том, что тест покажет неслучайность последовательности, тогда как в действительности она случайна, то есть последовательность имеет неслучайные свойства даже тогда, когда он сформирована «хорошим» генератором. Вероятность ошибки 2-го рода обозначается как b . Для тестаb - вероятность того, что тест покажет на случайность последовательности, когда она в действительности является неслучайной. То есть «плохой» генератор сформировал последовательность, которая, как будто обладает случайными свойствами. В отличие от a , ошибка 2-го рода b не является фиксированным значением. Она может принимать целый ряд различных значений, т.к. существует множество ситуаций, когда поток данных может быть неслучайным, и каждая из них может быть охарактеризована различными значениями b . Вычисление ошибки 2-го роду является более сложным заданием из-за существования большого количества различных типов неслучайности.
Одной из основных целей нижеописанных тестов является минимизация вероятности ошибки 2-го рода, иначе говоря, минимизация вероятности принятия последовательности, произведенной плохим генератором, за последовательность, произведенную хорошим генератором. Вероятность α и β связаны друг с другом и с длиной nпроверяемой последовательности: если два из этих значений определены, третье определяется автоматически. На практике обычно выбирают размер n и значение для α (вероятности ошибки 1-го рода). Тогда критическая точка для данной статистики выбирается так, чтобы получить наименьшее значение β (вероятность ошибки 2-го рода).
Каждый тест основан на вычислении значения тестовой статистики, которая является функцией данных. Если значение тестовой статистики есть S, а t – критическое значение, то вероятность ошибки 1-го рода и 2-го рода есть соответственно:
P(S>t||H0 истина) =P(отклонить H0 | H0истинна),
P(S≤ t || H0ложна) = P(принять H0 | H0 ложна).
Тестовая статистика использует вычисление значения P-value, которое констатирует силу доказательства против нулевой гипотезы, иначе говоря, P-valueесть вероятность того, что совершенный генератор случайных чисел произвел бы последовательность менее случайную, чем исследуемая, для типа неслучайности, проверяемого тестом. Если P-value для теста равно 1, то последовательность абсолютно случайна. P-value, равное 0, указывает, что последовательность абсолютно неслучайна. Для теста следует выбирать уровень значимости α. Если значение P-value больше или равно α, то принимается нулевая гипотеза, т.е. последовательность кажется случайной. Если значение P-value меньшеα, то нулевая гипотеза отклоняется, т.е. последовательность кажется неслучайной. Параметр α обозначает вероятность ошибки 1-го рода. Как правило, α выбирается в интервале [0.001,0.01].
· Значение α, равное 0.001, говорит о том, что из 1000 случайных последовательностей не прошла бы тест лишь одна. При P-value≥ 0.001 последовательность рассматривается как случайная с доверительностью 99.9%. При P-value<0.001 последовательность рассматривается как неслучайная с доверительностью 99.9%.
· Значениеα, равное 0.01, говорит о том, что из 100 случайных последовательностей не прошла бы тест лишь одна. При P-value≥ 0.01 последовательность рассматривается как случайная с доверительностью 99%. При P-value<0.01 последовательность рассматривается как неслучайная с доверительностью 99%.
По отношению к исследуемым последовательностям можно сделать следующие предположения.
· Равномерность. В любой точке при генерации последовательности случайных или псевдослучайных битов 0 и 1равновероятны и вероятности их появления равны 1/2. Ожидаемое число нулей (или единиц) равно n/2, где n– длина последовательности.
· Масштабируемость. Любой тест, применимый к последовательности, может также применяться к произвольной подпоследовательности. Если последовательность случайна, то любая ее подпоследовательность должна также быть случайна. Следовательно, любая подпоследовательность должна пройти все тесты на случайность.
· Полнота. Поведение генератора случайных чисел связано с начальным заполнением, поэтому неверно делать заключение о качестве генератора, основываясь на результатах анализа последовательности при каком-то одном начальном заполнении. Аналогично неверно делать заключение о генераторе случайных чисел, основываясь только на результатах анализа одного произведенного им фрагмента последовательности.
Таблица 2 показывает пошаговый процесс, позволяющий оценить конкретную двоичную последовательность.
Таблица 2. Процедура оценки
| Номер шага | Пошаговый процесс | комментарии |
| 1. | Постановка гипотезы | Предполагаем, что последовательность является случайной |
| 2. | Вычисление тестовой статистики последовательности | Проводим тестирование на битовом уровне |
| 3. | Вычисление P-value | P-valueÎ[0;1] |
| 4. | Сравнение P-valueс α | Задаем α, где αÎ[0.001;0.01]. Если P-value>α – тесты пройдены |
Дата добавления: 2018-06-01; просмотров: 984; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
