Функция распределения непрерывной случайной величины.
НСВ задается с помощью функции распределения
F(x)=P(X<x) или с помощью плотности распределения вероятности
f(x)=F`(x)
Функция плотности распределения имеет одно основное свойство
Если НСВ имеет ненулевую плотность на отрезке [a;b], вне этого отрезка на f(x)=0, то выполняется условие
Пример:
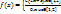Найти С
C= 
y=1/6(2x+3)
x 1; 2;
y 5/6; 7/6
T.K. F`(x)=f(x), то можно найти интегральную функцию распределения
Пример: Найти интегральную функцию распределения, если
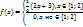
При x<1 
При 1<x<2 
При x>2 
x 1; 2; 1,5;
y 0; 1; 0,46.
Плотность распределения непрерывной случайной величины.
Плотностью распространения НСВ называется производная из функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.
F(x)= 
Свойства плотности распределения вероятностей НСВ:
1.Неотрицательная функция f(x)≥0
=1
Любая неотрицательная функция f(x), для которой 
=1, является плотностью распределения вероятностей некоторой непрерывно распределенной случайной величины.
Общий вид графика функции плотности распределения вероятностей непрерывной случайной величины:
Плотность равномерно распределенной НСВ: 
Математическое ожидание НСВ
М(x)= 
M(x)= 
M(x) = 
Дисперсия и СКВО НСВ
D(x)= 
D(x)= 
D(x)= 
СКВО-r(x)= 
D(x)= 
D(x)= 
СКВО= 
Нормальное распределение вероятностей непрерывной случайной величины.
|
|
|
Нормальное распределение
Определение. Случайная величина Х имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид:
f(x)= 
,
где σ и a– параметры распределения.
Определение. График функции f(x) называется нормальной кривой или кривой нормального распределения.
Методами дифференциального исчисления можно установить, что:
1)кривая симметрична относительно прямой х=a;
2)функция имеет максимум при х=a
f(a)= 
;
3)по мере удаления х от точки a функция убывает и при х→ ±∞ кривая приближается к оси Ох;
4)кривая выпукла вверх при х є (a– σ; a+ σ) и
выпукла вниз при х є (– ∞; a– σ) и х є (a+ σ; + ∞).
Кривая нормального распределения.
Числовые хар-ки:
M(x)=a
D(x)= 
СКВО= σ
Вероятность попадания в заданный интервал нормальной случайной величины.
Вероятность того, что случайная величина принадлежит интервалу (α;β)
P (α<x<β)=Ф( 
– Ф ( 
)
Пример:
Случайная величина распр. По случайному закону a=30, σ=10. Найдите вероятность того, что она принадлежит интервалу (10:50)
P (10<x<50) =Ф 
– Ф 
= 0,9544
Вычисление вероятности заданного отклонения нормальной случайной величины.
|
|
|
Вероятность того, что модуль отклонения случайной величины от своего мат.ожидания меньше некоторого значения.
Р(|Х-а|<δ)=2ɸ( 
)
Пример: найти вероятность того, что отклонение по абсолютной величине будет меньше 3-х для нормального распределения случайной величины с параметрами а=20, σ=3
Р(|Х-20|<3)=2ɸ( 
)=0,179*2=0,2358
Закон 
или 
: практически достоверно, что с Р=0,9993, что все значения нормального распределения случайной величины с параметрами а и σ заключены в интервале (а-3 
; а+3 ).
Пример: рост юношей некоторой возрастной группы имеет нормальное распределение с параметрами: а=174, =4. Найти все возможные значения роста юношей, max и min значениям.
(а-3 ; а+3 )=>(174-12; 174+12)=>(162; 186)
Дата добавления: 2018-05-31; просмотров: 862; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!