Анализ переходных процессов в электрической цепи
Переходный процесс происходит при внезапных (скачкообразных) изменениях структуры цепи или параметров ее элементов, в том числе, что наиболее важно, при отключении или включении (либо изменении параметров) задающих источников тока (напряжения).
Переходные процессы возможны только в цепях, где есть емкости (конденсаторы) и/или индуктивности (катушки индуктивности), т.е. элементы, способные запасать и отдавать энергию.
Запас энергии в конденсаторе определяется напряжением на нем, и это напряжение не может измениться мгновенно, в отличие от протекающего через конденсатор тока.
В катушке индуктивности запас энергии определяется током, протекающим через катушку, и этот ток не может измениться мгновенно, тогда как напряжение на катушке измениться может.
В классическом методе анализа реакцию цепи  на внезапное изменение ее состояния (структуры либо параметров) представляют в виде суммы свободной
на внезапное изменение ее состояния (структуры либо параметров) представляют в виде суммы свободной  и вынужденной
и вынужденной  составляющих, т.е.
составляющих, т.е.
 ,
,
где  ,
,  и
и  – токи либо напряжения.
– токи либо напряжения.
Вынужденная составляющая  , являясь реакцией цепи на внешнее воздействие, возникшее после коммутации (изменения состояния цепи), может быть определена одним из рассмотренных выше методов анализа цепи в установившемся режиме.
, являясь реакцией цепи на внешнее воздействие, возникшее после коммутации (изменения состояния цепи), может быть определена одним из рассмотренных выше методов анализа цепи в установившемся режиме.
При отыскании свободной составляющей  поступают следующим образом:
поступают следующим образом:
|
|
|
– одним из методов анализа цепи в установившемся режиме определяют токи индуктивностей  и напряжения емкостей
и напряжения емкостей  в момент времени, непосредственно предшествующий коммутации (
в момент времени, непосредственно предшествующий коммутации (  );
);
– для схемы, получившейся в результате коммутации, с учетом соотношений (1.1) – (1.3) составляется система интегро-дифференциальных уравнений;
– в результате решения этой системы уравнений относительно заданной неизвестной (напряжения или тока ветви) получают дифференциальное уравнение цепи;
– составляют характеристическое уравнение цепи, находят его корни и записывают общий вид свободной составляющей реакции цепи;
– постоянные интегрирования определяют из анализа цепи для момента времени  , непосредственно следующим за моментом коммутации, когда токи индуктивностей и напряжения емкостей еще не изменились, оставаясь равными соответственно
, непосредственно следующим за моментом коммутации, когда токи индуктивностей и напряжения емкостей еще не изменились, оставаясь равными соответственно  и
и  .
.
Классический метод анализа переходных процессов применяется для простейших цепей и при простых внешних воздействиях в виде скачка постоянного напряжения (тока) или включения в цепь источника гармонического сигнала. В общем случае используется операторный метод анализа, основу которого составляет преобразование Лапласа.
|
|
|
Как и в случае метода комплексных амплитуд, операторный метод анализа относится к символическим методам, в которых операции над функциями времени заменяются операциями над их символами (изображениями).
Прямое преобразование Лапласа

ставит в соответствие функции времени  функцию
функцию  комплексной переменной
комплексной переменной  . Функция
. Функция  называется изображением функции
называется изображением функции  , а сама функция
, а сама функция  по отношению к функции
по отношению к функции  – оригиналом. Оператор преобразования
– оригиналом. Оператор преобразования  можно рассматривать как обобщенную комплексную частоту (
можно рассматривать как обобщенную комплексную частоту (  – угловая частота;
– угловая частота;  – постоянное число).
– постоянное число).
Обратное преобразование Лапласа

(  ) ставит в соответствие функции
) ставит в соответствие функции  комплексной переменной
комплексной переменной  функцию
функцию  , для которой функция
, для которой функция  есть прямое преобразование Лапласа. Не всякая функция
есть прямое преобразование Лапласа. Не всякая функция  имеет обратное преобразование Лапласа. В общем случае существуют ограничения и при преобразовании функции
имеет обратное преобразование Лапласа. В общем случае существуют ограничения и при преобразовании функции  .
.
Прямое и обратное преобразования Лапласа обозначаются соответственно
 и
и 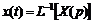
или

Некоторые свойства преобразования Лапласа (они же теоремы) приведены в табл. 1.1.
Все выражения для сопротивлений элементов  , установленные для обобщенных комплексных амплитуд, а также законы Ома и Кирхгофа и методы анализа цепей на их основе справедливы и для операторного метода, если под
, установленные для обобщенных комплексных амплитуд, а также законы Ома и Кирхгофа и методы анализа цепей на их основе справедливы и для операторного метода, если под  понимать не мнимую частоту, а оператор Лапласа. При этом начальные условия в виде токов индуктивностей и напряжений емкостей, существовавшие в момент коммутации, учитываются путем включения в схему дополнительных источников тока
понимать не мнимую частоту, а оператор Лапласа. При этом начальные условия в виде токов индуктивностей и напряжений емкостей, существовавшие в момент коммутации, учитываются путем включения в схему дополнительных источников тока  и источников напряжения
и источников напряжения  . В подавляющем большинстве случаев взаимные преобразования оригиналов и изображений можно выполнить без вычисления интегралов, используя готовые решения, сведенные в таблицы (некоторые из преобразований приведены в табл. 1.2).
. В подавляющем большинстве случаев взаимные преобразования оригиналов и изображений можно выполнить без вычисления интегралов, используя готовые решения, сведенные в таблицы (некоторые из преобразований приведены в табл. 1.2).
|
|
|
Таблица 1.1
| № | Операция | Оригинал | Изображение |
| 1 | Умножение на постоянный коэффициент k | 
| 
|
| 2 | Суммирование | 
| 
|
| 3 | Дифференцирование оригинала | 
| 
|
| 4 | Интегрирование оригинала | 
| 
|
| 5 | Изменение масштаба (  – постоянный коэффициент) – постоянный коэффициент)
| 
| 
|
| 6 | Сдвиг аргумента у оригинала (  ) )
| 
| 
|
| 7 | Сдвиг аргумента у изображения (  комплексное число) комплексное число)
| 
| 
|
Для отыскания оригиналов, изображения которых представлены в виде рациональных дробей вида
|
|
|
 либо
либо  ,
,
можно воспользоваться соответственно первой либо второй теоремами разложения:
 либо
либо  ,
,
где n – степень полинома  , которая должна быть больше степени полинома
, которая должна быть больше степени полинома  (не меньше в случае второй теоремы);
(не меньше в случае второй теоремы);  – производная по p полинома
– производная по p полинома  ;
;  – простые корни полинома
– простые корни полинома  ;
;  ,
,  – значения полиномов при
– значения полиномов при  .
.
Анализ переходных процессов операторным методом выполняется в следующей последовательности:
– в схеме цепи до коммутации одним из методов анализа установившегося процесса (например символическим) определяются токи индуктивностей и напряжения емкостей, которые наблюдались в момент, непосредственно предшествующий моменту коммутации (  );
);
– с учетом полученных начальных значений токов и напряжений составляется операторная схема цепи;
– по методу контурных токов или узловых напряжений составляется система уравнений в операторной форме;
– решается эта система уравнений относительно заданных неизвестных, представленных в операторной форме;
– используя табличные формулы перехода от изображения к оригиналу, получают решение в виде функций времени.
В качестве примера проведем анализ переходных процессов в цепи рис. 1.11,а при скачкообразном изменении постоянного напряжения задающего источника  от
от  В до
В до  В, т.е.
В, т.е.

Задача анализа: получить зависимости токов ветвей цепи от времени при  .
.

Рис. 1.11. Цепь с коммутируемым источником постоянного напряжения 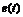
Поскольку коммутируется источник постоянного напряжения, начальные значения тока индуктивности  и напряжения емкости
и напряжения емкости  легко найти из анализа схемы рис. 1.11,а на постоянном токе (в установившемся режиме до коммутации):
легко найти из анализа схемы рис. 1.11,а на постоянном токе (в установившемся режиме до коммутации):
 ;
; 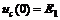 .
.
Составим операторную схему (рис. 1.11,б) цепи рис. 1.11,а, где



 ;
;  .
.
В соответствии с 1-й строкой табл. 1.2, где приведено изображение постоянной величины,
 ;
;  ;
;  .
.
Таблица 1.2
(a, b, c, β, γ,  – различные постоянные)
– различные постоянные)
| № | 
| 
|
| 1 | 
| 
|
| 2 | 
| 
|
| 3 | 
| 
|
| 4 | 
| 
|
| 5 | 
| 
|
| 6 | 
|  ; ; 
|
| 7 | 
| 
|
| 8 | 
|  ; ;  ; ;  ; ;

|
| 9 | 
|  ; ;  ; ;
 ; ; 
|
| 10 | 
|  ; ;
 ; ;  ; ;
 ; ;  ; ;
 ; ;  ; ;  ; ;  ; ;  ; ;  ; ; 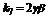 ; ; 
|
В схеме рис. 1.11,б преобразуем источник тока  в источник напряжения
в источник напряжения 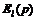 с параметром
с параметром
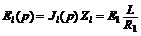 .
.
В результате получим схему рис. 1.11,в, которую можно описать следующей системой уравнений, составленной по методу контурных токов:
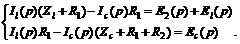
Решим эту систему уравнений относительно токов  и
и  :
:
 ;
;
 .
.
Представим эти функции в таком виде:
 ,
,
 ,
,
предварительно вычислив в соответствии с исходными данными (указаны на рис. 1.11,а) значения коэффициентов полиномов
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Определив корни  полинома
полинома  , запишем функции
, запишем функции  и
и  в табличной форме (см. табл. 1.2):
в табличной форме (см. табл. 1.2):
 ;
;  .
.
Если корни  получаются комплексно-сопряженными (как в рассматриваемом случае), то, чтобы исключить последующие преобразования выражений
получаются комплексно-сопряженными (как в рассматриваемом случае), то, чтобы исключить последующие преобразования выражений  и
и  , полином
, полином  представляют в таком виде:
представляют в таком виде:
 ,
,
в результате чего выражения  и
и  примут другие табличные формы:
примут другие табличные формы:
 ;
;  , (1.8)
, (1.8)
в соответствии с которыми (строка 6 при  и строка 8 табл. 1.2)
и строка 8 табл. 1.2)
 ; (1.9)
; (1.9)
 , (1.10)
, (1.10)
где  ;
;  ;
;  ;
;  ;
;  .
.
Вычислив все постоянные величины:
 ;
;  ;
;  ;
;  ;
; 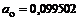 ;
;
 ;
; 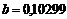 ;
;  ;
;  ;
;  ;
;  ,
,
временные зависимости токов  и
и  запишем в окончательном виде
запишем в окончательном виде
 [мА];
[мА];
 [мА]
[мА]
(угол φ измеряется в радианах). При расчете углов φ и ψ по формулам, приведенным в табл. 1.2, необходимо учитывать знаки числителя y и знаменателя x аргумента функции  , т.е. в какой четверти тригонометрического круга эта функция определена: если
, т.е. в какой четверти тригонометрического круга эта функция определена: если  , то
, то  (
(  может быть как положительным, так и отрицательным).
может быть как положительным, так и отрицательным).
Операторный ток  ветви, содержащей сопротивление
ветви, содержащей сопротивление 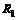 , как видно из рис. 1.11,в, равен разности токов
, как видно из рис. 1.11,в, равен разности токов  и
и  , описываемых выражениями (1.8), т.е.
, описываемых выражениями (1.8), т.е.
 .
.
Это выражение отличается от выражения для  только коэффициентом
только коэффициентом  , поэтому оригинал изображения
, поэтому оригинал изображения 



отличается от (1.10) исключительно значениями коэффициентов A, B и φ:

(в формулы для A, B и φ вместо b подставляется  ).
).
В результате выражение функции времени тока 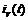 будет иметь вид
будет иметь вид
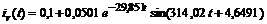 [мА].
[мА].

Рис. 1.12. Переходные процессы при коммутации источника постоянного напряжения
Графики функций  ,
,  и
и  приведены на рис. 1.12,а, б и в. Как видно из графиков, в цепи рис. 1.11,а (при указанных значениях параметров элементов) в результате коммутации источника постоянного напряжения происходит затухающий колебательный процесс с частотой
приведены на рис. 1.12,а, б и в. Как видно из графиков, в цепи рис. 1.11,а (при указанных значениях параметров элементов) в результате коммутации источника постоянного напряжения происходит затухающий колебательный процесс с частотой  Гц (
Гц ( 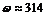 радиан/сек). При этом ток
радиан/сек). При этом ток  как при
как при  , так и при
, так и при  , тогда как
, тогда как  мкА, а
мкА, а 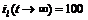 мкА, что, естественно, соответствует расчетным значениям (время
мкА, что, естественно, соответствует расчетным значениям (время  – это момент коммутации, а не начало оси абсцисс на графиках рис. 1.12). Первый максимум на графике
– это момент коммутации, а не начало оси абсцисс на графиках рис. 1.12). Первый максимум на графике  (рис. 1.12,б) соответствует моменту
(рис. 1.12,б) соответствует моменту  мсек, а на графике
мсек, а на графике  (рис. 1.12,в) – моменту
(рис. 1.12,в) – моменту 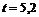 мсек.
мсек.
В качестве другого примера исследуем переходный процесс в той же цепи рис. 1.11,а, но при коммутации источника гармонического сигнала:

где  В;
В;  ;
;  Гц.
Гц.
Поскольку начальные условия нулевые, операторная схема цепи рис. 1.13,а примет вид, показанный на рис. 1.13,б, где

(см. строку 3 табл. 1.2 при  ).
).

Рис. 1.13. Цепь с коммутируемым источником гармонических колебаний 
Запишем систему уравнений по методу контурных токов:

и решим ее относительно неизвестных  и
и  :
:
 ;
;
 .
.
Запишем эти выражения в таком виде:
 ,
,
 ,
,
где
 ;
;  ;
;  ;
;
 ;
;  .
.
Определив корни  полинома
полинома  , представим функции
, представим функции  и
и  в табличной форме:
в табличной форме:
 ;
;  . (1.11)
. (1.11)
В соответствии с 10-й строкой табл. 1.2, учитывая, что коэффициент с в формулах (1.11) равен нулю (а в формуле для  равен нулю еще и коэффициент a), получим следующие выражения временных зависимостей токов:
равен нулю еще и коэффициент a), получим следующие выражения временных зависимостей токов:
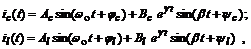 (1.12)
(1.12)
где  ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;
 .
.
После расчета значений всех постоянных величин –
 ;
; 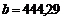 ;
;  ;
;  ;
;  ;
;
 ;
;
 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
; 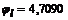 ;
; 
– функции (1.12) примут окончательный вид:

Как видно из этих выражений и соответствующих графиков на рис. 1.14,б и в, при коммутации источника гармонического сигнала в цепи рис. 1.13,а ток емкости (и индуктивности) будет состоять из двух, наложенных друг на друга, составляющих, одна из которых представляет собой вынужденные гармонические колебания с частотой  а другая – свободную составляющую в виде затухающих колебаний с частотой
а другая – свободную составляющую в виде затухающих колебаний с частотой  .
.

Рис. 1.14. Переходные процессы при коммутации источника гармонического сигнала
Если требуется получить временные зависимости напряжений на емкости и индуктивности, то в соответствии с формулами (1.2) и (1.3) необходимо выполнить соответственно операции интегрирования и дифференцирования токов  и
и  :
:
 ;
;  ,
,
где  – напряжение на емкости в момент коммутации.
– напряжение на емкости в момент коммутации.
Так, к примеру, в схеме рис. 1.11,а на основании выражений (1.9) и (1.10) получаются следующие функции:
 ;
;  ,
,
где  ;
;  .
.
Функции  и
и  можно также найти, исследуя операторную схему цепи относительно операторных напряжений
можно также найти, исследуя операторную схему цепи относительно операторных напряжений  и
и  с последующим преобразованием их выражений.
с последующим преобразованием их выражений.
Задание 1
Методом узловых напряжений или контурных токов получить выражения и определить значения напряжений и токов ветвей цепи рис. 1.15 соответствующего варианта (в1 – в10).
Параметры элементов цепи:  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 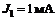 ;
;  .
.

Рис. 1.15. Схемы электрических цепей к заданию 1
Задание 2
1. Проанализировать цепь рис. 1.16 соответствующего варианта методом узловых напряжений (в1 – в5) или контурных токов (в6 – в10), получив выражение напряжения ветви  (
(  ).
).
2. По данным параметров элементов цепи рассчитать значение функции передачи  на частоте
на частоте  и представить это значение в показательной форме:
и представить это значение в показательной форме:
 ,
,
где  ,
,  .
.
3. Вычислить комплексную амплитуду напряжения
 ,
,
где  ,
,  .
.

Рис. 1.16. Схемы электрических цепей к заданию 2
Данные элементов схем рис. 1.16,в1 – в5:  ;
; 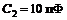 ;
;  ;
;  ;
; 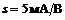 ;
; 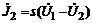 для в1–в2 и
для в1–в2 и  для в3–в5.
для в3–в5.
Данные элементов схем рис. 1.16,в6 – в10:  ;
; 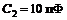 ;
;  ;
;  ;
;  ;
;  ;
; 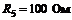 ;
;  ;
;  .
.
Данные задающего источника:  .
.
Задание 3
1. Исследовать переходный процесс в цепи рис. 1.17 соответствующего варианта (в1 – в10), получив выражения токов  и
и  .
.
2. Представить графики зависимостей токов  и
и  как функций времени
как функций времени  .
.
Исходные данные.
Параметры элементов схемы:  мкФ;
мкФ;  Гн;
Гн;  кОм;
кОм;  Ом;
Ом;  кОм;
кОм;  кОм.
кОм.
Задающее воздействие:
 либо
либо 
где  В;
В;  В;
В;  В;
В;  ;
;  Гц.
Гц.

Рис. 1.17. Схемы электрических цепей к заданию 3
Дата добавления: 2018-06-27; просмотров: 232; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
