Решение систем линейных алгебраических уравнений
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
 . (1)
. (1)
Если хотя бы одно из чисел 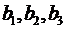 не равно нулю, то такая система называется неоднородной.Если же
не равно нулю, то такая система называется неоднородной.Если же  , то такая система называется однородной.
, то такая система называется однородной.
Решением системы (1) называется упорядоченная совокупность чисел  , которая при подстановке в систему обращает все уравнения системы в верные равенства.
, которая при подстановке в систему обращает все уравнения системы в верные равенства.
Если система имеет решение, то она называется совместной, если не имеет решения – то несовместной.Если система имеет единственное решение, то она называется определенной, если более одного решения, то – неопределенной.
Матричный метод решения СЛАУр
Запишем систему линейных уравнений в матричной форме. Введем обозначения:
 ,
,  ,
,  .
.
где А – матрица коэффициентов системы,
Х – вектор-столбец неизвестных,
В – вектор-столбец свободных членов.
Тогда систему (1) можно кратко записать в матричной форме  .
.
Умножив обе части равенства слева на матрицу  , получим
, получим
 , но
, но 
следовательно,  . Эта формула дает решение системы (1) в матричной форме.
. Эта формула дает решение системы (1) в матричной форме.
Пример 1
Решить систему  матричным методом.
матричным методом.
Решение
Матрица этой системы  ,
,
обратная матрица имеет вид 
Применяя формулу  , получим
, получим

Следовательно,  ,
, 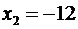 ,
,  .
.
Формулы Крамера для решения СЛАУр
Если определитель системы  , то эта система имеет единственное решение, которое можно получить по формулам Крамера:
, то эта система имеет единственное решение, которое можно получить по формулам Крамера:
|
|
|
 ,
,
где
 .
.
В знаменателях этих формул стоит определитель системы  , а в числителях – определители, которые получаются из определителя системы
, а в числителях – определители, которые получаются из определителя системы  заменой коэффициентов при соответствующих неизвестных столбцом свободных членов.
заменой коэффициентов при соответствующих неизвестных столбцом свободных членов.
Пример 2
Решить систему  по формулам Крамера.
по формулам Крамера.
Решение
Формулы Крамера:  . Вычислим определители:
. Вычислим определители:
 ,
,
 , тогда
, тогда
 ,
,  ,
,  . Итак,
. Итак,  ,
,  ,
,  .
.
Контрольное задание № 3
В данном задании используются индивидуальные параметры: m–число букв в Фамилии студента, n–число букв в полном Имени студента.
1.1. Найти значение матричного многочлена  , если
, если  ,
,  ,
, 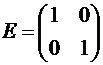 .
.
1.2. Вычислить определитель по правилам треугольника и диагоналей и разложением по любой строке (или столбцу):  .
.
1.3. Найти матрицу обратную к матрице  и проверить выполнение равенства
и проверить выполнение равенства  .
.
1.4. Решить систему линейных алгебраических уравнений тремя способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса:  .
.
Часть 4. Задача линейного программирования
Рассмотрим графический метод решения на следующем примере.
Задача №1. Для производства двух препаратов A и B химическое производство использует три вида сырья:
| Виды сырья
| Норма расхода сырья(кг/стандарт) | Общее количество сырья(кг) | |||
| А | В | ||||
| I II III | 12 4 3 | 4 4 12 | 300 120 252 | ||
| Прибыль от реализации 1 стандарта (усл.ед/станд) | 30 | 40 | |||
Необходимо составить план выпуска, при котором прибыль от реализации выпущенной продукции будет максимальна.
Обозначим х1-количество стандартов препарата А, х2-количество стандартов препаратаВ.
Целевая функция (общая прибыль) оптимизируется на максимум Q=30x1+40x2  max.
max.
По каждому виду сырья составляются ограничения в форме неравенств, а на переменные накладывается условие неотрицательности:

Алгоритм графического решения ЗЛП:
1) строят прямые линии по условиям-ограничениям;
2) находят полуплоскости, определяемые каждым ограничением;
3) находят многоугольник решений (пересечение полуплоскостей);
4) строят систему параллельных линий Q=const, проходящих через многоугольник;
5) находят точку, в которой значение целевой функции Q максимально;
6) определяют оптимальный план (х1*;х2*) и значение целевой функцииQ для оптимального плана.
Решим задачу №1 графически согласно приведенному алгоритму:
- неравенства заменим на равенства
|
|
|
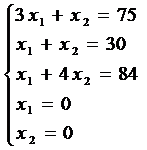
|

|
|
|
- определяем координаты точки В, решив систему:
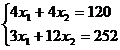

 х* = (12;18) – оптимальный план.
х* = (12;18) – оптимальный план.
- максимальная прибыль: Qmax = 30 · 12 + 40 · 18 = 1080 усл. ед.).
Прямая Q=constможет пересекать допустимую область в точке, по лучу, по отрезку. Допустимая область не всегда является ограниченной областью.
Индивидуальное задание №4
Решить задачи с двумя переменными графическим методом (табл. 1) в соответствии со своим номером в списке группы.
Таблица 1. Варианты задания 1
| Вариант | Задача | Вариант | Задача |
| 1 | 
| 6 | 
|
| 2 | 
| 7 | 
|
| 3 | 
| 8 | 
|
| 4 | 
| 9 | 
|
| 5 | 
| 10 | 
|
| 11 | 
| 17 | 
|
| 12 | 
| 18 | 
|
| 13 | 
| 19 | 
|
| 14 | 
| 20 | 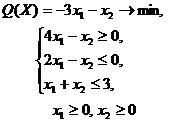
|
| 15 | 
| 21 | 
|
| 16 | 
| 22 | 
|
| 23 | 
| 27 | 
|
| 24 | 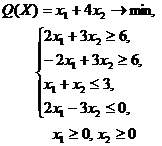
| 28 | 
|
| 25 | 
| 29 | 
|
| 26 | 
| 30 | 
|
Дата добавления: 2018-05-13; просмотров: 221; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 , который указывает направление перемещения прямой
, который указывает направление перемещения прямой
 - перемещая прямую
- перемещая прямую 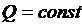 в направлении вектора
в направлении вектора  , видим, что макс. значение целевая функция принимает в точке “B”
, видим, что макс. значение целевая функция принимает в точке “B”