Свойства определённого интеграла.
1)постоянный множитель можно выносить за знак интеграла
2)интеграл от алгебраической суммы 2х функций равен такой же сумме интегралов от этих функций
3)Если отрезок интегрирования разбит на части,то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей,т е при любых а,в,с
4)Если на отрезке а,в где а<в,f(x)<=g(x),т е обе части неравенства можно почленно интегрировать
5)если функция у=f(x) непрерывна но отрезке а,в где а<в то найдётся такое значение ξ Э(в друг сторону(принадлежит)) отрезку а,в что(напиши формулой) интеграл ф от х д х=ф(ξ)(в-а)
10Выпуклость и вогнутость функции. Точки перегиба.
У=ф от х назыв выпукл на промеж х если её гафик на этом промежутке лежит ниже касат-й проведенной к нему в любой точке промеж.
Вогнута если график ф-ии на эт пром леж выше касат проведен к точке эт промеж
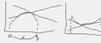дост.усл выпукл,вогн ф-ии:Если 2я произв дважды диффер-й фии положит на промеж х то ф-я вогнутая
Если 2я произв отриц на пром х то ф-я выпукла на эт пром
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение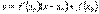 
. Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. 
|
|
|
Итак, уравнение кривой имеет вид y = f(x). Обозначим 
ординату касательной, соответствующую абсциссе x. Тогда 
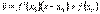. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет . 
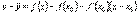Разность f(x) – f(x0) преобразуем по теореме Лагранжа 
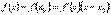, где c между x и x0.
Таким образом,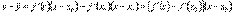 
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: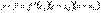 
, где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
Предположим, что x>x0. Тогда x0<c1<c<x, следовательно, (x – x0) > 0 и (c – x0) > 0. Поэтому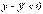 
.
Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь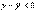 
.
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Точка в котор выпуклость фии смен вогнут или наоб наз т перегиба
Усл сущ т перег :если 2я произв дважды диф фии в т х0=0 и проходя через эту т меняет знак то х0 т перег
Асимптоты графика функции.
.Прямая L назыв ассимптотой граф у=ф от х если расст от т на граф до прямой L стремится к 0 при неогр удалении эт точки от начала корд
|
|
|
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е.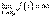 
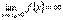или 
или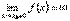 
. Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное, если прямая x = x0 является асимптотой, т. о. 
.
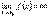Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
|
|
|
Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда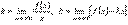 
. Аналогичное утверждение верно и при x → –∞. 
Первообразная и её свойства. Неопределённый интеграл и его свойства. Таблица интегралов.
неопр интегралом от фии ф от х д хназыв совокупн всех первообразн
| Основные св-ва неопределённого интеграла:
 Мы поможем в написании ваших работ! | |||