Возрастание и убывание функции. Экстремумы функции. Связь с первой и второй производной
Замечательные пределы.
1 замечательный предел.

Возьмем круг радиуса 1, обозначим
радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда

Разделим все на 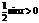 и получим:
и получим:

Т.к.  , то по признаку существования пределов следует
, то по признаку существования пределов следует 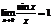 .
.
2 замечательный предел.

Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:

Если x→∞, то n→∞, тогда

По признаку о существовании пределов:

5. Непрерывные функции и их свойства. Точка разрыва функций и их классификация.
Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:

Это означает:
- функция определена в точке х0 и в ее окрестности;
- функция имеет предел при х→х0
- предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство.
Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0
Точки разрыва функции – это точки в которых нарушается непрерывность функции.
Точка разрыва х0 называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)
|
|
|
 и
и 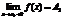
При этом, если:
- А1=А2 то точка х0 называется точкой устранимого разрыва;
- А1≠А2 то точка х0 называется точкой конечного разрыва.
|A1 – A2| называется скачком функции.
Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.
Производная от функции. Дифференцируемость функции. Дифференциал.
Производной функции y=f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.

Производная функции f(x) есть некоторая функция
f ’(x), произведенная из данной функции.
Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемойв этом интервале.
Операция нахождения производной называется дифференцированием.
Дифференциал функцииy=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).
Иначе. Дифференциал функцииравен произведению производной этой функции на дифференциал независимой переменной.
Скорость изменения функции-физ см произ
|
|
|
Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.
Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).
Тангенс угла наклона касательной прямой-геом см пр y = f ’(x0) · (x – x0) + f(x0).
Функция fl называется касательной к f в точке x0. Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.
Теорема Ферма.
Если функция у = f (х), определенная в интервале (а ; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).

Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [а ; b] и дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0.
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).
|
|
|

Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что

Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ
 Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.
Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.
8
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа  или .
или . 
Пусть a является некоторым конечным действительным числом или равно бесконечности.
Если  и
и  , то
, то  ; по теор.лагранжа
; по теор.лагранжа
Если  и
и 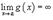 , то аналогично
, то аналогично  .
.
Возрастание и убывание функции. Экстремумы функции. Связь с первой и второй производной
большему значению аргумента соответствует большее значение функции.
Необх.усл.возр,уб ф-ии:Если ф-я возр(уб)на промеж. Х то её произв не отриц(не полож) на эт промеж
Т.х0 наз т мах ф-ии если сущ такая окрестн в т х0 что для люб х их эт окрестн f(x) < f(x0). И тоже самое для мин
|
|
|



В 1 рис есть касат в этих т и произ =0 ,во 2 нет произв
В т экстремума произв= либо 0 либо не сущ
Если ф-я деффер-ма то в окрестн т экстремума выполн теорема Ферма.Значит по т Ферма произв в т экстремума=0
В точках где произ=0 или не сущ- крит т
Достаточн условие сущ т экстремума:если при перех через т х0 произв ф-ии меняет знак то х0-т экстремума
(если знак с + на – то мах и наоб)
Если в т х0 1я произв дважды дифференцируемой ф-ии =0 а вторая произ меньше 0 то это т макс и наоб
Дата добавления: 2018-05-13; просмотров: 353; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
