Свойства плотности распределения случайного вектора.
1. 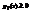
2.  .
.
 .
.
Теорема 1. Пусть 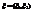 —непрерывный случайный вектор. Тогда случайные величины
—непрерывный случайный вектор. Тогда случайные величины  и
и  — непрерывны, причем
— непрерывны, причем 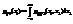 ,
, 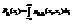 .
.
3.  , где
, где  —множество из пространства
—множество из пространства 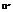 .
.
Теорема Пуассона.
Теорема. Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n изменяется таким образом, что некоторое событие А появится ровно k раз в n независимых испытаниях стремится к величине 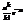 , то есть
, то есть 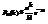 .
.
▲По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях


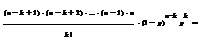

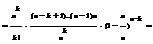
Схема независимых испытаний Бернулли. Полиномиальное распределение.
Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей.  ,
,  , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний.
, p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний.
Опр. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.
Элементарным исходом будет являться: (w1,w2,…,wn),  . Всего таких исходов 2n.
. Всего таких исходов 2n. 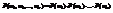 . (1)Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли.
. (1)Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли. 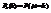 — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие
— вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие 
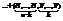 . По теореме сложения получим
. По теореме сложения получим

Таким образом, получим 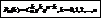 —формула Бернулли.
—формула Бернулли.
Случайные величины. Функции распределения и их свойства.
|
|
|
Опр. Случайной величиной Хназывается функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.
Множество значений случайной величины обозначается Ωх.
Опр. Функцией распределения случайной величины Хназывается функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.  .
. 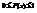 .
.
Свойство 1. Функция распределения F(x)–неубывающая функция, т.е. для 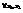 таких что x1<x2
таких что x1<x2 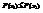 .Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е.
.Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е. 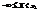 , представим в виде объединения двух несовместимых событий
, представим в виде объединения двух несовместимых событий 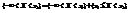 . Тогда по теореме сложения вероятностей получим
. Тогда по теореме сложения вероятностей получим  , т.е.
, т.е.  . Поскольку
. Поскольку  , то
, то 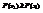 .
.
Дискретные случайные величины. Законы распределения биномиальное, геометрическое и Пуассона.
Опр. Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно.
Опр. Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.  , причем
, причем 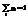 .
.
|
|
|
Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения 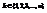 с вероятностями
с вероятностями  .
. 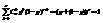
Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения 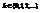 с вероятностями
с вероятностями  . Обозначают
. Обозначают 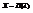 , т.е. случайная величина Х имеет распределение Пуассона с параметром λ.
, т.е. случайная величина Х имеет распределение Пуассона с параметром λ. 
Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения  с вероятностями
с вероятностями  , где q=1-p.
, где q=1-p.
 .
.
Дата добавления: 2018-05-13; просмотров: 340; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
