Точечные и интервальные оценки параметров распределения. Доверительная вероятность (надёжность) и доверительный интервал.

Стр 1 из 4Следующая ⇒

Предмет математической статистики. Генеральная и выборочная совокупности. Статистический ряд распределения выборки. Полигон и гистограмма. Эмпирическая функция распределения.

…	,
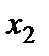
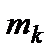
…		(24)
…

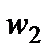
Математическая статистика — раздел математики, посвященный математическим методам систематизации, обработки и использовании статистических данных для научных и практических выводов. Основное отличие математической статистики от теории вероятностей в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и характеристик по результатам экспериментов. Одним из основных способов сбора статистических данных является выборочный метод — метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку. Всю исследуемую совокупность однородных объектов называют генеральной совокупностью, а множество объектов, случайно отобранных из генеральной совокупности, — выборочной совокупностью или просто выборкой. Объемом генеральной или выборочной совокупности называют число всех ее объектов. При составлении выборки пользуются двумя основными способами: повторным (отобранный объект обследуют, и снова возвращают в генеральную совокупность) и бесповторным (обследуемый объект не возвращается в генеральную совокупность). На практике обычно пользуются бесповторным способом. Для того чтобы свойства выборки достаточно хорошо отражали свойства генеральной совокупности, выборка должна быть репрезентативной (или представительной), то есть когда каждый объект генеральной совокупности имеет одинаковую возможность попасть в выборку. Пусть из генеральной совокупности извлечена выборка, причем значение изучаемого признака наблюдалось раз, — раз, … , — 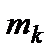раз, и 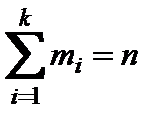— объем выборки. Наблюдаемые значения называют вариантами, а последовательность вариант, записанных в возрастающем порядке — вариационным рядом. Числа называют частотами (или весами), а их отношение к объему выборки, то есть — относительными частотами (или частостями), при этом . В случае, когда количественный признак является дискретным его варианты и соответствующие им частоты или относительные частоты представляют в виде таблицы

…	.
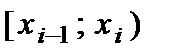
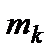
…		(25)
…

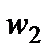
называемой статистическим распределением выборки или статистическим дискретным рядом. Графическое представление ряда (24) дает полигон частот (или относительных частот), представляющий собой ломаную линию, состоящую из отрезков, соединяющих точки (или точки ). Нетрудно заметить полную аналогию между статистическим распределением выборки и законом распределения дискретной случайной величины, столь лишь разницей, что в данном распределении вместо возможных значений случайной величины фигурируют варианты, а вместо соответствующих вероятностей — относительные частоты. В силу этой аналогии по известному статистическому распределению можно по тем же формулам, что и для дискретного распределения, найти выборочные аналоги математического ожидания и дисперсии. В случае большого количества вариант или непрерывного распределения признака статистическое распределение задают в виде интервального статистического ряда:

В качестве частоты (частости ), соответствующей интервалу , принимают сумму частот (частостей), попавших в этот интервал. Отметим, что в общем случае длины интервалов могут быть между собой не равны. 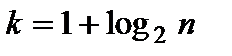Однако в случае дискретного признака с большим количеством вариант (то есть большом объеме выборки) интервалы обычно берут одинаковой длины, которую можно определить по формуле Стерджесса: где — разность между наибольшей и наименьшей вариантами признака, — объем выборки, — число интервалов За начало первого интервала рекомендуется брать величину Интервальный ряд (25) графически изображают в виде гистограммычастот (частостей) — ступенчатой фигуры, состоящей из прямоугольников, основаниями которых служат частичные интервалы длины а высоты равны отношению — плотности частоты ( — плотности относительной частоты). Очевидно, площадь гистограммы частот равна объему выборки, а площадь гистограммы относительных частот равна единице. Гистограмма относительных частот является статистическим аналогом плотности распределения вероятностей генеральной совокупности. Одним из способов обработки вариационного ряда является построение эмпирической функции распределения. 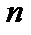Эмпирической (статистической) функцией распределения выборки называется функция где — объем выборки, — число вариант меньших 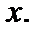Эмпирическая функция распределения 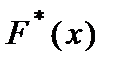является оценкой теоретической функции распределения случайной величины . Различие заключается в том, что в теории вероятностей определяет вероятность события а — его относительную частоту.

26. Выборочные характеристики статистического распределения (выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое отклонение, средняя ошибка, коэффициент вариации, начальный и центральный моменты r-го порядка, асимметрия и эксцесс выборки, мода и медиана).

Числовые характеристики статистического распределения. Для справки приведем некоторые числовые характеристики, аналогичные тем, что в теории вероятностей определялись для случайных величин. Пусть статистическое распределение выборки объема имеет вид (24).Выборочным средним называется среднее арифметическое всех значений выборки[1]: Для непрерывно распределенного признака формулы для выборочных средних будут такими же, но за значения надо брать не концы промежутков 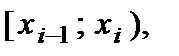а их середины 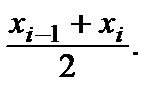Выборочной дисперсией, обозначаемой (или ) называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней , то есть Выборочное среднее квадратическое отклонение определяется формулой При обработке малых выборок (объема ) используется величина то есть которая называется исправленной выборочной дисперсией.Следовательно, величина называется исправленнымвыборочным средним квадратическим отклонением.

Точечные и интервальные оценки параметров распределения. Доверительная вероятность (надёжность) и доверительный интервал.

Пусть мы имеем некоторую выборку из генеральной совокупности с известным законом распределения и требуется оценить параметр по данным выборки. Статистической оценкой неизвестного параметра генеральной совокупности называется его приближенное значение вычисленное по данным выборки и зависящее только от них. Чтобы оценка давала хорошее приближение, она должна быть несмещенной, эффективной и состоятельной. 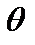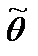Статистическая оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть Оценка называется эффективной, если при данном объеме выборки она имеет наименьшую дисперсию. Оценка называется состоятельной, если при она стремится по вероятности к оцениваемому параметру то есть при любом предел Это означает, что с увеличением объема выборки мы все ближе приближаемся к оцениваемому параметру то есть практически достоверно Заметим, что состоятельность оценки обязательна для любого правила оценивания (несостоятельные оценки не используются). Точечной называют оценку, которая определяется одним числом. Например, рассмотренные в п. VI оценки неизвестных параметров нормального распределения: выборочное среднее , исправленные выборочные дисперсия и среднее квадратическое отклонение , являются точечными. Точечные оценки неизвестного параметра хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно с какой точностью они дают оцениваемый параметр. При малых объемах выборки точечные оценки могут значительно отличаться от оцениваемого параметра. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра не одним числом, а целым интервалом В этой связи, наряду с точечными оценками пользуются еще и интервальными, которые определяются двумя числами — концами интервала. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал внутри которого с заранее выбранной вероятностью находится точное значение оцениваемого параметра Интервал 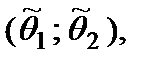покрывающий с вероятностью 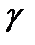истинное значение параметра называется доверительным интервалом,а вероятность — доверительной вероятностью или надежностью оценки. Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки то есть интервал вида такой, что Число 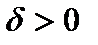характеризует точность оценки: чем меньше разность 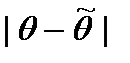, тем точнее оценка. Обычно надежность оценки выбирается заранее и зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, игрушки и т.д. Обычно доверительную вероятность 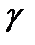берут равной 0,9, 0,95, 0,99 или 0,999. Разность показывает, с какой вероятностью заключение о надежности оценки ошибочно, и называется уровнем значимости. В зависимости от конкретного случая уровень значимости принимают равным 0,1, 0,05, 0,01 или 0,001.

28. Доверительный интервал для оценки математического ожидания нормального распределения (t-распределение Стьюдента). Доверительный интервал для математического ожидания 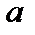при неизвестном среднем квадратическом отклонении нормально распределенного признака определяется из двойного неравенства (27),где — исправленное среднее квадратическое отклонение, значение параметра определяется по таблице приложения 3 критических точек распределения Стьюдента[2] по заданной доверительной вероятности (или уровню значимости ) и числу степеней свободы . Отметим, что при больших выборках (объема ) 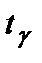и число , найденное по таблице значений функции Лапласа, практически совпадают.Доверительный интервал для математического ожидания при известном среднем квадратическом отклонении нормально распределенного признака определяется из двойного неравенства(26),где — объем выборки, — выборочное среднее, — аргумент функции Лапласа , при котором — определяется при заданной надежности по таблице приложения 2 значений функции Лапласа.