Интегральная теорема Лапласа.
Вероятность А от m1 до m2 раза при n испытаниях.
Р(m1,m2)-?
Р(m1,m2)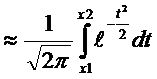 
, где 
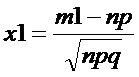
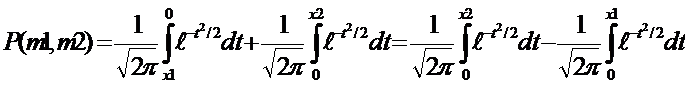
нечетная
Пример 1. Вероятнос 
ть появления события в каждом из 100 независимых
испытаний =0,8. Найти вероятность того, что событие появится:
а)ровно 75 раз; б)не менее 75 и не более 90; в)менее 75 раз.
n=100 p=0.8 q=1-p=0.2
m=75
a) P75; 100= 
x=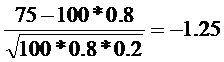 
φ(-1.25)=0.1826
P=0.1826/4=0.05
б) Р75; 90= 
x1=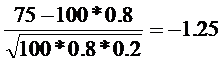 
Ф(x1)=0.1826
x2= 
Ф(x2)=0.4938
Р75; 90=0.4938-0.1826=0.3112
в) P75; 100=Ф(x2)-Ф(x1)
= 
= 
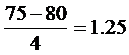
P75; 100=Ф(5)+Ф(1,25)=0,5+0,3944=0,8944
Вероятное отклонение относительной частоты от показаний в независимых испытаниях
, 
вероятность того, что относительная частота отклонится от постоянной не более чем на 
Применим интегральную Т. Лапласа
Таким образом мы получаем, что вероятность отклонения = 
Пример 1. Вероятность появления событий в каждом из 625
независимыхиспытаний=0,8. найти вероятность того, что
относительная частота появления событий отклоняется от его
вероятности по абсолютной величине не более чем на 0,04.
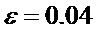n=625 p=0.8 q=1-p=0.2
x= 
Ф=0,4938
Р=2*0,4938=0,9876
Пример 2. Вероятность появления событий в каждом из независимых испытаний
=0,5. Найти число испытаний, при которых с вероятность 0,7698 можно
ожидать, что относительная частота появления событий отклонится от
его вероятности по абсолютной величине не более чем на 0,02
|
|
|
2Ф(х)=0,7698
=0,02
р=0,5 q=0.5
Ф=0,7698/2=0,3849
х=1,2=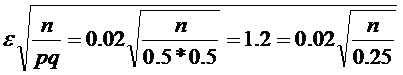 
1,2= 
n=900
Пример 3. Вероятность появления события в каждом из 400 испытаний =0,8.
Найти такое положение 
, чтобы с вероятностью 0,99. Абсолютная
величина отклонения относительной частоты по абсолютной величине
не привышает 
.
p=0.8 q==0.2
Ф(х)=0,99/2=0,495
2Ф=0,99
n=400
2.58= 
=0.0516
Формула Пуассона
Если n велико, а p вероятность в каждом испытании мала (p<0.1), то формула Лапласа дает неоправданно большую погрешность. В таких случаях для вычисления того, что в независимых испытаниях событие наступит m раз при n испытаниях вычисляется по формуле: где
a=np Pm; n = 
Пример 1. Издано 100 тыс. экземпляров книг. Вероятность брака составляет
0,0001. Найти вероятность того, что в тираже 5 бракованых книг.
n=100000 p=0.0001 m=5 a=10
ℓ 
=0.000045
Пример 2.
а) n=12 m=7 p=0.6 q=0.4
б) n=200 m=1 p=0.6 q=0.4
P(1; 200)= 
P(1; 200)=0
P(111; 130)=Ф(х2)-Ф(х1)=Ф(1,44)+Ф(1,3)=0,4265+0,4032=0,8297
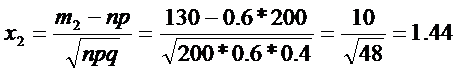
в) Р(0; 10)=Ф(х2)-Ф(х1)
х2=-17,14 х1=-1,43
г) Р(115; 200)=Ф(х2)-Ф(х1)
=0,03 n=600 p=0.6 q=0.4
P=2*0.1808=0.36
=? 
=? n=600 P=0.993
|
|
|
P(m1; m2)=Ф(х2)-Ф(х1)
р=0,6 q=0.4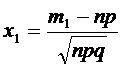 
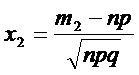
х=0,49
п=1866,24
Случайные величины и их распределение.
Случайная величина (СВ) – величина, которая может принять то или иное значение, наперед неизвестное.
Случайные величины бывают: 1)дискретные – такие, возможные значения которых можно перечислить (кол-во выбитых очков); б)непрерывные – те, возможные значения которых заполняют некоторый промежуток.
Чтобы задать СВ нужно задать возможные значения этой величины и соответствующей вероятности. Если СВ дискретная, то законом для нее может быть таблица
∑ Pi=1
| x | x1 | x2 | … | xn |
| Pi | P1 | P2 | … | Pn |
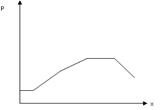
Если рисовать график, по ОХ откладывать возможные значения, а по ОУ соответ вероятности и соответ точки соединить. График называется полигоном
Интегральная функция распределения, ее свойства.
Интегральной функцией распределения называется функция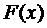 
определяющая вероятность того, что СВ х примет значение <X
F(x)=P(X<x)
Свойства функции:
1. 
2. 
функция неубывающая
3. 
Мат ожидание
Для того, чтобы задать случайную величину нужно задать закон определения случайной величины. Для дискретной случайной величины закон может быть задан в виде таблицы.
|
|
|
| x | x1 | x2 | … | xn |
| Pi | P1 | P2 | … | Pn |
СВ характеризуется числовыми характеристиками. К ним относится математическое ожидание.
Свойства мат ожидания:
1. М(С)=С, х=С, М(х)=С*1=С
2. постоянный множитель можно выносить за знак мат ожидания.
М(Сх)=СМ(х), х=Сх
М(Сх)=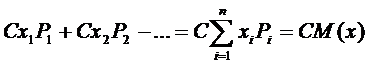 
3. 
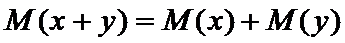
| y | y1 | y2 |
| q | q1 | q2 |
| x | x1 | x2 |
| P | P1 | P2 |
| x+y | x1+ y1 | x2 + y2 | x2 + y1 | x2 + y2 |
| Pq | P1 q1 | P1 q2 | P2q1 | P2 q2 |
4. 
Дисперсия
Дисперсия – это матожидание квадрата отклонения СВ от матожидания.
матожидание есть величина постоянная
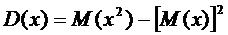
Дата добавления: 2018-05-13; просмотров: 281; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!