Формула полной вероятности и формула Байеса.

Классическое и статистическое определение вероятности.

Основным понятием ТВ является событие. Событие – это есть всякий факт или явление, которое может произойти в данном эксперименте или при данных условиях. Все явления рассматриваются в двух условиях:

1. детерминированные

2. стохастические

события бывают: 1) достоверные, которые в данных условиях или эксперименте обязательно наступают; 2) невозможное, которое в данных условиях произойти не может; 3) случайное, которое может произойти, а может не произойти.

Обозначают буквами А и В.

Событие А и В называют совместными если наступление одного не исключает появление другого. А и В несовместные если появление одного из них исключает возможное появление другого.

Событии бывают А и (не А). Равновозможные, когда нет оснований предполагать, что одно из них произойдет более вероятно, чем другое. Единственновозможные (А – «5», В – «4», С – «3», Д – «2», Е – н/я) такие события образуют полную группу событий: равновозможные, попарно несовместные.

А или В = А+В=С – произойдет А или В или А и В вместе.

АUВ =С

А и В = АUВ =А*В =С

Р(А)= классическая вероятность события А = , где n – это число.

0<= P <=1

Классическое определение вероятности имеет свои недостатки: n и m бывает определить трудно, а иногда невозможно, поэтому идут по другому пути.

Статистическое определение вероятности. Пусть мы проведем многократно некоторый эксперимент и связанное с ним событие А и наблюдаем. Произошло А, то +, нет - . проводим его n раз, где m – количество раз появления А. На численном эксперименте при большом n показываем, что это отношение в каждом конкретном случае колеблется возле какого-то числа.

W(A)= называют относительной частотой события А и в реальных задачах эту частоту принимают за вероятность.

W(A)= Р(А)

События бывают зависимые и независимые. А и В называют независимыми если вероятность одного из них не зависит от наступления другого. А и В называют зависимыми если вероятность одного зависит от наступления или ненаступления другого. Для зависимых событий вводят понятие условной вероятности.

или Р(А/В)

Теоремы сложения и умножения вероятностей.

1. Вероятность наступления события А или В, т.е. вероятность суммы событий равна сумме вероятностей этих событий если события несовместные.

2. Если события совместные, то Р(А+В)=Р(А)+Р(В)-Р(АВ)

3. Вероятность событий А и В = Р(АВ)=Р(А)*Р(В) для независимых.

4. вероятность событий А и В =Р(А) (В)=Р(В)* для зависимых событий.

5. Р(А)+Р( )=1

Р(А)=Р, Р( )= 1-р=q

Примеры.Произвели 3выстрела. Определить событие В состоит в том, что

ровно одно попадание.

А1 – попал 1 – не попал

А2 2

А3 3

В= А1 2 3 + 1 А2 3 + 1 2 А3

Определить событие С не менее двух попаданий

С= А1 А2 3 + 1 А2 А3 + А1 2 А3 + А1 А2 А3

Пример 2. В книге 185 стр. какова вероятность, что случайно открытая

страница имеет порядок заканчивающийся на 2.

А – открыли n=185 А= =

m=19

пример 3. Вероятность поломки станка по вине рабочего = 0,04; а

вероятность поломки без рабочего = 0,06. Какова вероятность

поломки

А – по вине В – сам по себе

С = А+В = 0,04+0,06=1

Элементы комбинаторики.

1. Перестановки – это комбинации, которые состоят из одних и тех же элементов и отличаются только порядком их расположения.

=n!=1*2*3…n

1, 2, 3 =3!=1*2*3=6

2*1*3=6

3*2*1=6 6

1*3*2=6

2*3*1=6

3*1*2=6

2. Размещение – это комбинации, составленные из n разных элементов по m в каждом, отличающиеся или составом элементов или их порядком.

n=3 m=2

A 1, 2

2, 1

1, 3 6

3, 1

2, 3

3, 2

3. Сочетания – это комбинации составленные из n разных элементов по m в каждом, отличающиеся хотя бы одним элементом.

Пример 1. В конкурсе принимают участие 5 студентов. Порядок их

выступления определяется жеребьевкой. Сколько существует

вариантов порядка их выступления.

5!=120

Пример 2. Расписание занятий 1-го дня состоит из трех пар. Определить

количество вариантов расписания при выборе из 10 дисциплин.

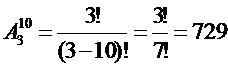
Пример 3. В шахматном турнире участвуют 20 человек. Сколько партий они

сыграют, если между 2-мя участниками должна сыграться 1

партия.

Пример 4. Монету бросили 2 раза. Какова вероятность, что хотя бы 1 раз

появится герб.

Герб-герб

Герб – решка

Решка – решка вероятность 3/4

Решка – герб

Пример 5. В коробке 6 пронумерованных кубиков. На удачу достают по 1

кубику. Какова вероятность, что они будут попадаться в порядке

возрастания.

n=6! m=1 =

Пример 6. В пачке 20 перфокарт, помеченных номерами от 101 до 120 и

произвольно расположенные. На удачу достают 2 перфокарты.

Какова вероятность, что эти карты будут с номерами 101 и 120.

n=20 m=2 Р=

пример 7. В ящике 15 деталей, 10 из них окрашены. На удачу достают 3.

Какова вероятность, что они будут окрашены.

n=15= m=10=

Пример 8. В ящике 100 деталей, 10 из них бракованные. Достаем 4. Какова

вероятность, что среди них нет: а) браков; б) годных

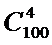n= m=

а)

б)

Пример 9. Вероятность сдачи экзамена на «5»=0,3; «4»=0,45; «2»=0,1;

«н\я»=0,05. Какова вероятность, что студент получит

положительную оценку.

1-(0,3+0,45+0,1+0,05)=0,1

Р(А) = 0,3+0,45+0,1=0,85

Пример 10. Вероятность попадания в мишень при одном выстреле для 1-го

стрелка=0,8 для 2-го =0,9. Найти вероятность того, что: а)оба

попадут в мишень; б)только первый; в)только второй; г)один

стрелок попадет; д)никто не попадет; е)хотя бы один попадет.

А-первый В-второй

А=0,8 В=0,9

=0,2 =0,1

Несовместные, независимые

а)А*В=0,8*0,9=0,72

б)А и =0,8*0,1=0,08

в) и В=0,2*0,9=0,18

г) *В или *А=Р(А )+Р( В)=(0,8*0,1)+(0,2*0,9)=0,08+0,18=0,26

д) и =0,2*0,1=0,02

е)1-0,02=0,98

Пример 11. Для некоторой местности среднее количество ясных дней в июле

25. Какова вероятность, что первые 2 дня будут ясные.

Р(А)= что второй день ясный – В

т. к. один день уже убрали

Р(АВ)=Р(А)*Р(В)=

Пример 12. Вероятность того, что событие появится хотя бы 1 раз в трех

независимых испытаниях=0,936. Найти вероятность появления

события в одном испытании.

Р(А)= q=1-p

Да=p нет=q (куб-количество испытаний)

0,936= q=0,4

p=1- q=0,6

Формула полной вероятности и формула Байеса.

Рассмотрим такую схему: пусть событие А наступает если произойдет одно из событий Н , … составляющие полную группу событий. Известно, Р(Н ), Р( )….Р( ). Известны условные вероятности , …. . 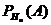Как найти вероятность события А. Р(А)=?

Т. Вероятность события Р(А)= Р(Н ) + Р( ) +…+Р( )

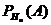
По условию Р(А) может наступить при АН1 или АН2…..АНn. Р(Н ), Р( ) или Р( ) несовместны, поэтому несовместны и АН1, АН2…..АНn. Поэтому Р(А)=Р(АН1)+ Р(АН2)+….+Р(АНn)= Р(Н ) + +Р( ) +…+Р( )

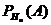
А и Н , попарно зависимы.

Пример1. В цехе 3 типа станков автоматов, на которых производятся детали.

Производительность их одинакова, но качество работы разное.

Известно, что станки 1 типа производят 94% деталей отличного

качества, 2-90%, 3 – 85%. Все детали сложены на складе.

Определить вероятность того, что взятая деталь окажется

отличного качества, если 1 типа – 5 шт., 2 типа – 3 шт., 3 типа – 2

шт.

пусть А – деталь стандартная

изготовили: 1 станок Н

2 станок

3 станок Н3

Р(Н )= Р( )= Р(Н3)=

=0,94 =0,9 =0,85

Р(А)= Р(Н ) + +Р( ) +Р(Н3)* * =1/2*0,94+3/10*0,9+1/5*0,85=0,91

Правило Байеса. Имеется полная группа событий, известны их вероятности. Производится опыт в результате появления события А. какие вероятности имеют события в связи с появлением события А. другими словами, вероятность

Р( )=

Пример 1. Изделие проверено на стандарт 2-мя товароведами. Вероятность

того, что изделие попадет 1-му=0,55 второму = 0,45. вероятность

того, что изделие будет стандартным, если его проверил 1-ый=0,9

второй 0,98. После проверки изделие оказалось стандартным. Какова

вероятность, что его проверил 2-ой.

Н - первый товаровед Р(Н )=0,55

- второй товаровед Р( )=0,45

=0,9 =0,98

Пример 2. В партии 600 лампочек. 200 изготовлены на 1 заводе, 250 на 2, 150

на 3. Вероятность того, что лампочки стандартные изготовлены

1=0,97; 2=0,91; 3=0,93. Взята 1 лампочка, которая оказалась

стандартной. Какова вероятность, что она выполнена на 1 заводе.

- первый завод 200/600=1/3

- второй завод 250/600

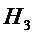- третий завод 150/600

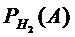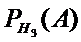=0,97 =0,91 =0,93

- ?

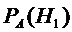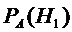Локальная теорема Лапласа.

При достаточно больших m и n пользоваться формулой Лапласа сложно. Теорема Лапласа позволяет найти приближенные значения вероятности того, что событие произойдет m раз при n.

, где при этом

Ее значения находят по таблице (стр. 99)

Свойства:

1) четная

2) max x=0

3) при x>3

Дата добавления: 2018-05-13; просмотров: 262; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!