Интегральная функция распределения дискретной случайной величины.
Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x вероятность того, что случайная величина X примет значение, меньше x.
Свойства интегральной функции
1. Значения интегральной функции принадлежат отрезку [0..1]. 
2. F(x) — неубывающая функция. 
3. Если возможные значения случайной величины принадлежат интервалу (a,b) то
Следствие 1. Вероятность того, что случайная величина примет значение из интервала (a,b) равна приращению интегральной функции на этом интервале.
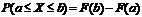
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.
Следствие 3. Если возможные значения случайной величины расположены по всей числовой оси, то справедливо:
Дифференциальная функция распределения непрерывной случайной величины.
Дифференциальной функцией распределения f(x) называют первую производную от интегральной функции распределения.
Свойства:
1. Дифференциальная функция неотрицательна.
2. Несобственный интеграл от дифференциальной функции в пределах 
равен единице. 
Теорема. Вероятность того, что случайная величина примет значение X, принадлежащее интервалу (a,b), равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b.
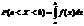
Геометрический смысл: Вероятность того, что случайная величина примет значение X, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Х, кривой распределения f(x), и прямыми x=a и x=b;
|
|
|
Замечание. Если f(x) — четная функция и концы интервала симметричны относительно начала координат, то
Нахождение интегральной функции распределения по известной дифференциальной функции.
Зная дифференциальную функцию распределения f(x) можно найти интегральную функцию F(x) по формуле:
Вероятностный смысл дифференциальной функции распределения.
По определению дифференциальной функции 
или
.
Разность 
определяет вероятность того, что случайная величина примет значение из интервала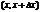 
Итак, дифференциальная функция распределения определяет плотность распределения вероятности для каждой точки x.
Замечание 1.
Вероятность того, что случайная величина примет значение, принадлежащее интервалу 
приближенно равна (с точностью до бесконечно малых высшего порядка относительно 
) произведению плотности вероятности в точке x на длину интервала .
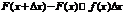
Замечание 2.
Вероятность того, что случайная величина примет значение, принадлежащее интервалу 
приближенно равна площади прямоугольника со сторонами и f(x).
Дата добавления: 2018-05-13; просмотров: 542; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!