Визначення оптимальних стратегій і ціни гри складає процес знаходження розв’язку гри.
Теорема 2. Усяка матрична гра з нульовою сумою має розв’язок в змішаних стратегіях.
Теорема 3. Для того щоб  була ціною гри, а
була ціною гри, а 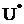 і
і  - оптимальними стратегіями, необхідно і достатньо, щоб виконувались нерівності
- оптимальними стратегіями, необхідно і достатньо, щоб виконувались нерівності
 і
і 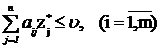 .
.
Теорема 2 дає відповідь на питання про існування розв’язку гри.
Теорема 4 дає відповідь на питання, як знайти це рішення для ігор
 ,
,  і
і 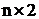 .
.
Теорема 4. Якщо один із гравців застосовує оптимальну змішану стратегію, то його виграш дорівнює ціні гри  незалежно від того, з якими частотами буде застосовувати другий гравець стратегії, що ввійшли в оптимальну (у тому числі і чисті стратегії).
незалежно від того, з якими частотами буде застосовувати другий гравець стратегії, що ввійшли в оптимальну (у тому числі і чисті стратегії).
Приклад 1.Знайти розв’язок гри, заданою матрицею 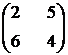 , і дати геометричну інтерпретацію цього розв’язку.
, і дати геометричну інтерпретацію цього розв’язку.
Передусім перевіримо наявність сідлової точки в даній матриці. Для цього знайдемо мінімальні елементи в кожному з рядків (2 і 4) і максимальні елементи в кожному зі стовпців (6 і 5).
Отже, нижня ціна гри 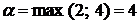 , а верхня ціна гри
, а верхня ціна гри 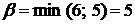 .
.
Так як  , то розв’язком гри є змішані оптимальні стратегії, а ціна гри
, то розв’язком гри є змішані оптимальні стратегії, а ціна гри  знаходиться в межах
знаходиться в межах 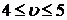 .
.
Припустимо, що для гравця  стратегія задається вектором
стратегія задається вектором  . Тоді на підставі теореми 4 при застосуванні гравцем
. Тоді на підставі теореми 4 при застосуванні гравцем 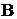 чистих стратегії
чистих стратегії  чи
чи  гравець
гравець  одержить середній виграш, що дорівнює ціні гри, тобто
одержить середній виграш, що дорівнює ціні гри, тобто
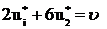 , (при стратегії
, (при стратегії  )
)
 , (при стратегії
, (при стратегії  )
)
Крім двох рівнянь відносно  і
і  додамо рівняння, що зв’язує частоти
додамо рівняння, що зв’язує частоти  і
і 
 .
.
Розв’язуючи отриману систему трьох рівнянь з трьома невідомими, знаходимо  .
.
|
|
|
Знайдемо тепер оптимальну стратегію для гравця 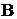 . Нехай стратегія для даного гравця задається вектором
. Нехай стратегія для даного гравця задається вектором 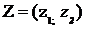
Тоді

Розв’язуючи систему рівнянь, що складається з будь-яких двох рівнянь, узятих з останньої системи, одержимо  . Отже, розв’язком гри є змішані стратегії
. Отже, розв’язком гри є змішані стратегії  та
та  , а ціна гри
, а ціна гри  .
.
Геометрична інтерпретація розв’язку гри
На площині 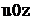 уведемо систему координат і на осі
уведемо систему координат і на осі  відкладемо відрізок одиничної довжини
відкладемо відрізок одиничної довжини 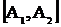 , кожній точці якого поставимо у відповідність деяку змішану стратегію
, кожній точці якого поставимо у відповідність деяку змішану стратегію  .
.
Зокрема, точці  відповідає стратегія
відповідає стратегія  , точці
, точці  – стратегія
– стратегія  .
.
У точках  і
і  побудуємо перпендикуляри на отриманих прямих будемо відкладати виграш гравців.
побудуємо перпендикуляри на отриманих прямих будемо відкладати виграш гравців.
 На першому перпендикулярі (у даному випадку він збігається з віссю
На першому перпендикулярі (у даному випадку він збігається з віссю 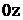 ) відкладемо виграш гравця А при стратегії
) відкладемо виграш гравця А при стратегії  , а на другому – при стратегії
, а на другому – при стратегії  . Якщо гравець А застосовує стратегію
. Якщо гравець А застосовує стратегію  , то його виграш дорівнює 2 при виборі гравцем В стратегії
, то його виграш дорівнює 2 при виборі гравцем В стратегії  , а стратегії
, а стратегії  виграш гравця А дорівнює 5. Числам 2 і 5 на осі
виграш гравця А дорівнює 5. Числам 2 і 5 на осі 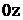 відповідають точки
відповідають точки  і
і  .
.
Рис.1.
Якщо ж гравець  застосовує стратегію
застосовує стратегію  , то його виграш при стратегії
, то його виграш при стратегії  гравця В дорівнює 6, а при стратегії
гравця В дорівнює 6, а при стратегії  він дорівнює 4. Ці два числа визначають дві точки
він дорівнює 4. Ці два числа визначають дві точки  та
та  на перпендикулярі, побудованому у точці
на перпендикулярі, побудованому у точці  . З'єднуючи між собою точки
. З'єднуючи між собою точки  з
з  та
та  з
з  , одержимо дві прямі, відстань до який від осі
, одержимо дві прямі, відстань до який від осі  визначає середній виграш за будь-якої комбінації відповідних стратегій.
визначає середній виграш за будь-якої комбінації відповідних стратегій.
|
|
|
Відстань від будь-якої точки відрізка  до осі
до осі  визначає середній виграш
визначає середній виграш  за будь-якої комбінації стратегій
за будь-якої комбінації стратегій  і
і  (з частотами
(з частотами  і
і  ) і стратегії
) і стратегії  гравця
гравця  . Ця відстань дорівнює математичному сподіванню
. Ця відстань дорівнює математичному сподіванню
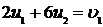
Аналогічно, середній виграш 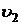 при застосуванні стратегії
при застосуванні стратегії  визначається ординатами точок, що належать відрізку
визначається ординатами точок, що належать відрізку 

Ординати точок, що належать ламаній  , визначають мінімальний виграш гравця
, визначають мінімальний виграш гравця  при застосуванні ним будь-яких змішаних стратегій. Ця мінімальна величина є максимальною в точці
при застосуванні ним будь-яких змішаних стратегій. Ця мінімальна величина є максимальною в точці  , отже, цій точці відповідає оптимальна стратегія
, отже, цій точці відповідає оптимальна стратегія  , а її ордината дорівнює ціні гри
, а її ордината дорівнює ціні гри  . Координати точки
. Координати точки  знаходимо як координати точки перетину прямих
знаходимо як координати точки перетину прямих  та
та  . Відповідні три рівняння мають вид
. Відповідні три рівняння мають вид

Розв’язуючи останню систему рівнянь, одержуємо
 .
.
Аналогічно знаходиться оптимальна стратегія для гравця 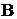 .
.
Для її визначення маємо рівняння
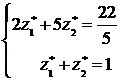
звідки  .
.
Отже, рішенням гри є змішані стратегії
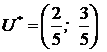 та
та  ,
,
а ціна гри  .
.
До такого висновку ми прийшли і вище.
Узагальнюючи викладені вище результати знаходження розв’язку гри  , , можна вказати
, , можна вказати
|
|
|
Етапи знаходження розв’язку гри  чи
чи 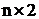 графічним методом
графічним методом
1. Будують прямі, що відповідають стратегіям другого (першого) гравця.
2. Визначають нижню (верхню) границю виграшу.
3. Знаходять дві стратегії другого (першого) гравця, яким відповідають дві прямі, що перетинаються в точці з максимальною (мінімальною) ординатою.
4. Визначають ціну гри й оптимальні стратегії.
Приклад 2. Знайти розв’язок гри, заданою матрицею

Рішення. Прямі  ,
,  і
і  відповідають стратегіям, а ламана
відповідають стратегіям, а ламана 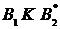 – нижній границі виграшу гравця
– нижній границі виграшу гравця  . Гра має розв’язок
. Гра має розв’язок  .
.

Приклад 3.Знайти розв’язок гри, заданої матрицею

Рішення. Матриця має розмірність 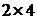 . Будуємо прямі, що відповідають стратегіям гравця
. Будуємо прямі, що відповідають стратегіям гравця  Ламана
Ламана 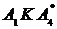 відповідає верхній границі виграшу гравця
відповідає верхній границі виграшу гравця  , а відрізок
, а відрізок  – ціні гри.
– ціні гри.

Розв’язок гри:  .
.
Дата добавления: 2018-05-13; просмотров: 523; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
