Задачі теорії ігор і лінійне програмування
Гра як об’єкт дослідження
Грають не тільки діти. Ігор в нашому житті так багато, а самі вони такі різноманітні та захоплюючі, що ми просто не в змозі залишатися осторонь: граємо самі, вболіваємо за інших гравців, обговорюємо ігрові стратегії, і нарешті, придумуємо нові ігри. Ігри як об'єкт дослідження цікавлять психологів, тому що гра виявляє глибокі і неочевидні психологічні сторони людини. До ігор небайдужі солідні бізнесмени: їх ділові ігри часто допомагають досягти успіху в своїй справі, а гральний бізнес, як прийнято вважати, сам по собі обіцяє чималі доходи. Зрозуміло, і математики бачать в грі не тільки розвагу, але і благодатний грунт для побудови складних моделей, узагальнень і теорій.
Давайте спробуємо уявити, що саме є гра і які ігрові проблеми можуть представляти інтерес для математика. Далі ми розглянемо класичне завдання теорії ігор і її рішення, самі побудуємо нескладну математичну модель ігрового процесу і з'ясуємо, яким чином в рамках цієї моделі можна судити про інтерес до гри з боку гравця. На закінчення обговоримо корисність нашої моделі для розробників нових ігор.
Різноманіття ігор створює певні складнощі у визначенні самого поняття гри. Щоб уникнути двозначності, спробуємо спочатку зробити ряд спостережень, що відносяться до найбільш відомих нам ігор.
1. Будь-яка гра має мету. Якщо грає одна людина, то і мета гри одна. Якщо ж учасників більше, ніж один, то у кожного з них є власна мета. Цілі деяких учасників гри (гравців) можуть співпадати.
|
|
|
2. У грі обов'язково присутні ресурси, які якимось чином розподілені між учасниками. Кожен учасник має можливість розпоряджатися своїми ресурсами на свій розсуд. Ресурси завжди обмежені, але можливо, поновлювані по ходу гри.
3. В ході гри відбувається зміна ігрових ситуацій. Для одного гравця кожна ситуація характеризується певною кількістю ресурсів, що належать йому, і певним прогресом в досягненні своєї мети. Ігрову ситуацію, в якій мета досягнута, а ресурси ще не закінчилися, назвемо виграшем. Ситуація, в якій навпаки, закінчилися ресурси, а мета ще не досягнута, назвемо програшем.
4. Будь-який гравець завжди має можливість вийти з гри (кинути гру). Він також має право зіграти повторно. Реальні наслідки цих дій не мають відношення до гри як такої.
Прочитавши перші три пункти спостережень, Ви напевно про себе відзначили, що гра мало чим відрізняється від реального життя. Справедливо! Але саме останній пункт дає нам ключ до розуміння суті гри. Гра як вид діяльності надає нам унікальну можливість зануритися в ті або інші незвичні, часто екстремальні ситуації, відчути смак боротьби, радість успіху, гіркоту поразки – і все це з мінімальним ризиком яких би то не було негативних наслідків в реальному (неігровому) житті.
|
|
|
Крім того, часто в грі ми отримуємо ті навики поведінки і той досвід, які потрібні нам і за межами гри. Гра дуже схожа на модель реального світу. Модель, в якій зібрані найбільш яскраві і цікаві сторони нашого життя, і відкинуте те, що нудно. Модель, яку можна вивчити і випробувати багато разів. Модель, яку ми самі вибрали і від якої завжди можемо відмовитися, якщо вона перестане бути нам цікавою. Чи варто дивуватися із загальної популярності і різноманіття ігор?
Математики відносно ігор пішли ще далі. Образно кажучи, вони взагалі стерли грань між грою і життям. Іншими словами, дослідника-математика не цікавить, чи отримає переможець гри своє золото насправді, або віртуально, чи страчуватимуть переможеного явно або відберуть у нього віртуальне життя. Математику цікаво лише те, як поведуться гравці під час гри, які вони прийматимуть рішення, як витрачати ресурси і чи буде їх поведінка оптимальною для досягнення мети гри.
Більш того, коли математику пропонують серйозне неігрове завдання, то він починає її розглядати в рамках деякої моделі, що ідеалізується, тим самим роблячи із завдання своєрідну іграшку. "Погравши" з нею і зробивши необхідні висновки, він переконує споживача в їх справедливості відносно проблеми в цілому.
|
|
|
"Теорія ігор - розділ математики, предметом якого є вивчення математичних моделей прийняття оптимальних рішень в умовах конфлікту. При цьому під конфліктом розуміється всяке явище, в якому беруть участь різні сторони, названі безліччю гравців і наділені не співпадаючими інтересами..."
(Шкільна енциклопедія математика, під ред. С.М.Нікольського, М.: 1996, С.380)
"Гра (у математиці - прим. автора) - це математична модель колективної поведінки, що ідеалізується: декілька гравців впливають на результат гри, причому їх інтереси різні."
(Е.Мулен, Теорія ігор з прикладами з математичної економіки, М.: Мир, 1985, С.10)
Гра для математика – це перш за все модель, і як модель вона може мати і має цінність в повсякденній практиці. Суперечності між необхідністю досягнення деякої мети і обмеженістю ресурсів, конфлікти між інтересами учасників, необхідність приймати рішення і виробляти власну стратегію – виникають всюди в нашому житті: у економіці і управлінні, в сім'ї і школі, в політиці і спорті і так далі. Математична теорія ігор у багатьох випадках здатна вказати оптимальний шлях до вирішення цих протиріч, а в деяких випадках – прогнозувати їх результат.
|
|
|
Дилема ув'язненого
Дослідження ігор ми почнемо з класичного завдання, відомого в літературі під назвою "дилема ув'язненого" (Льюс і Райфа, 1957). Суть "гри" полягає в наступному. Двоє злочинців потрапляють в камеру для ув’язнених на тривалий термін. У кожного з них є тільки два варіанти поведінки (дві стратегії): або поводитися мирно, або стати агресором і спробувати підпорядкувати собі сусіда по камері. Складність вибору стратегії, проте, полягає в тому, що кожен ув'язнений не знає, як поведеться сусід по камері. Значить, йому необхідно оптимізувати свій вибір в умовах неповної інформації про майбутню гру.
Щоб зробити правильний вибір, найпростіше порівняти передбачуваний виграш (або програш) для обох стратегій. Оскільки стратегій дві і злочинців теж двоє, то можливих результатів гри буде 2*2=4. Зручно зобразити їх у вигляді таблиці (матриці) розміром 2 на 2.
Таблиця 1. Результати гри залежно від стратегій гравців
|
| Гравець 2 | ||
| Мир | Агресія | ||
| Гравець 1 | Мир | 2 2 | 0 3 |
| Агресія | 3 0 | 1 1 | |
Передбачуваний виграш в чисельному виразі для першого гравця показаний в лівому верхньому кутку комірки, а для другого – в правому нижньому її кутку. Оцінки достатньо умовні, але відображають якісну сторону конфлікту. Зокрема, з таблиці ми бачимо, що найбільший виграш (3 одиниці) виходить у агресора, якщо його агресія направлена на миролюбного сусіда. З іншого боку, при взаємній агресії гравці отримують не так вже багато (1), в порівнянні з тим, що вони мали б, будучи сусідами мирно (2).
Ми також бачимо, що агресивна стратегія є домінуючою: незалежно від того, яку стратегію вибрав суперник, вигідно поводитися агресивно. На цій підставі можна стверджувати, що в цій грі агресивна стратегія оптимальна. Зробимо важливе зауваження: ми припускаємо, що в цій грі гравці позбавлені можливості вести переговори для вироблення сумісної стратегії. Якби переговори були допустимі, то слід було б чекати прояву мирної стратегії з обох боків.
Наведений приклад відноситься до найбільш простого типу ігрових завдань, в яких всі можливі результати гри можна перебрати в комірках так званої платіжної матриці. Звідси і назва цього класу завдань – матричні ігри. Простота полягає і в одноразовому виборі стратегії. Інакше кажучи, кожен гравець робить в цій грі тільки один "хід", а сама гра на цьому закінчується. Складніші варіанти ігор можуть припускати нескінченну кількість стратегій, безліч ходів, можливість тимчасового об'єднання (кооперації) або навіть об'єднання на всю гру (коаліції) гравців для вирішення сумісних завдань. У деяких іграх гравці дізнаються правила гри не перед грою, а в процесі гри (так звані динамічні ігри), що створює додаткові складнощі в пошуку оптимальної стратегії.
Хорошим полем діяльності для фахівців з теорії ігор є політика. Парламентські і президентські вибори, конфлікти політичних партій і фракцій, формування блоків і коаліцій – практично вся активність гравців-політиків націлена на досягнення своїх цілей у великій політичній грі.
Азартні ігри
Строго кажучи, азартні ігри не є предметом дослідження теорії ігор. Цей факт легко пояснити: у азартній грі, як правило, результат залежить не від умілих або продуманих дій гравця, а від випадкових чинників. Інтерес до азартної гри часто підігрівається високими ставками або іншими зовнішніми стимулами, що відводять дослідника убік від ігрових проблем. Проте, іноді про азартні ігри говорять в хорошому сенсі слова: азартні – тобто цікаві, захоплюють, не залишають нікого байдужим. З цієї точки зору, дослідження азартних ігор представляє безперечний інтерес для творців нових ігор, а значить і для математиків, що закладають фундамент нових розробок.
Насправді, які ігри понад усе захоплюють і чому? Причин тому може бути декілька. Тут і новизна ігрових ситуацій, і своєрідність оформлення, і можливість реалізувати свої здібності. Не менш істотна динамічність гри: велика кількість екстремальних ситуацій з неочевидним результатом для всієї гри. Але що означає динамічність гри на мові математики? Чи можна її зміряти? І чи можна говорити про динамічність ігор взагалі, порівнюючи такі різні ігри, якими є, наприклад, футбол і шахи? Спробуємо відповісти на всі ці питання, запропонувавши математичну модель ігрового процесу.
Як вже наголошувалося, в грі може брати участь декілька гравців і їх оцінка динамічності гри, взагалі кажучи, може розрізнятися. Тому ми говоритимемо про сприйняття одного з гравців, маючи на увазі його конкретну мету і відповідно його ресурси в даній грі.
Гравець може володіти набором ресурсів, кожен з яких в тому або іншому ступені необхідний для досягнення мети і кожен з яких може бути зміряний кількісно. Типовим ресурсом шахіста є набір фігур, які він може пожертвувати в ході гри і при цьому поставити мат супротивникові. Іншим його ресурсом є контрольний час, за який він зобов'язаний зробити певну кількість ходів. Як би не була кількість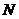 
ресурсів 
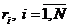у розпорядженні гравця, ми завжди можемо вести мову про деяку узагальнену скалярну величину – ресурс 
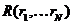, який і відображатиме загальний стан з ресурсами у гравця на даний момент гри. Зокрема, на початку гри ми можемо покласти для визначеності 
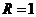, тоді як 
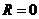означатиме відсутність ресурсів, необхідних для продовження гри.
Нам буде потрібно також іншу скалярну величину, по якій ми могли б судити про прогрес на шляху до ігрової мети. Назвемо її цільовою функцією і позначимо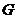 
(позначення є скороченням англійських слів: resource = ресурс, goal = мета). На початку гри ми покладемо 
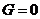– це означає, що для досягнення мети ще нічого не зроблено. Досягненню мети відповідатиме вибране нами для визначеності значення 
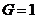. Для шахіста величина 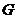, швидше за все, відповідає так званій позиційній перевазі, яка врешті-решт приводить до перемоги. Зміряти його непросто, але в принципі, можливо. Для футбольної команди 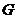є функцією різниці забитих і пропущених м'ячів, а також часу, який залишився до закінчення матчу. (Подумайте самі, як записати цю функцію?)
За розвитком гри або за ігровим процесом, нам зручніше стежити, спираючись на змінну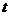 
. Це не обов'язково час, адже в багатьох іграх час строго не враховується. Точніше, ми вважатимемо, що кожному значенню 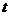відповідає своя ігрова ситуація, яка характеризується цілком певним запасом ресурсів у кожного з гравців і цілком певним прогресом в досягненні своєї мети кожним з них. Величина 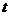в ігровому процесі змінюється монотонно від 
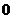(початок гри) убік 
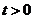. Вона може бути безперервною, як у футбольному матчі, або дискретною, як в шахах, – залежно від конкретної гри. Завершенню гри (для нашого гравця) відповідає таке значення 
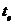, при якому виконана одна з двох умов: або 
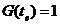(досягнення мети, виграш), або 
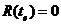(вичерпання ресурсів, програш). Що стосується так званого "нічийного результату", то ми не розглядатимемо його окремо. Врешті-решт, кожен гравець (команда) ще до початку гри знають, влаштовує їх нічия чи ні. Значить, вони мають право вважати нічию рівносильною виграшу або програшу відповідно.
Таким чином, в області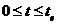 
ми можемо описувати ігровий процес з позицій конкретного гравця двома функціями: 
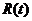і 
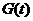. На графіках 1, а-б наведені приклади ігрових процесів, які закінчилися виграшем і програшем.
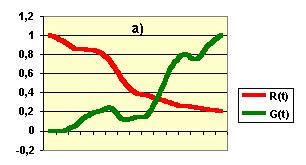
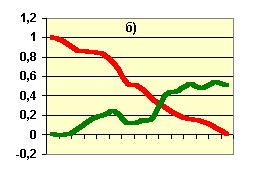
Рис.1. Ігровий процес з: а) виграшем; б) програшем.
Для того, щоб судити про динаміку ігри, а значить, в якійсь мірі і про інтерес гравця до неї, нам треба оцінити, кому в процесі гри належала ініціатива, чи переходила вона з рук в руки або результат гри був ясний із самого початку. Введемо в розгляд функцію ініціативи, поклавши її за визначенням рівною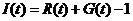 
. Відповідно до цього визначення і спираючись на розглянуті вище граничні значення функцій 
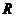і 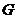, можна відмітити, що на початку гри 
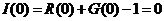. В кінці гри, у разі виграшу 
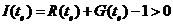, а у разі програшу – 
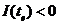. В процесі гри зростання функції 
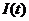ми пов'язуємо з посиленням позицій гравця, а зміну знаку цієї функції означає перехід ініціативи з рук в руки.
Можна також відзначити, що область значень 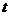, при яких 
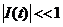має сенс ігрових відрізків боротьби на рівних, тоді як відхилення і вихід 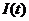за межі вказаної області означатиме значну перевагу сил однієї із сторін. Нарешті, ми можемо дати кількісну оцінку динамічності 
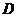гри, розглядаючи її як відношення суми довжин відрізків боротьби на рівних до загальної довжини ігрового процесу 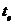. Щоб довести оцінку величини 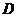до числа, нам доведеться замінити якісний критерій 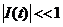на кількісний: 
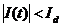, де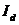 
– додатне порогове значення (константа для наший моделі).
Само собою, величина 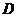залежить не тільки від правил гри, але і від індивідуальних здібностей гравця, його старання і навіть везіння. Тому перше ж завдання, яке доводиться вирішувати творцеві або організаторові нової гри, полягає в тому, щоб зацікавити нею і новачка, і "професіонала". Якщо в грі беруть участь протиборчі сторони, то шукана рівновага сил досягається підбором команд (учасників) одного рівня, віднесенням їх в певні ліги і так далі Якщо ж учасник гри один, як це часто буває в комп'ютерних іграх, то сама гра повинна мати можливість налаштування на різні рівні майстерності.
Отже, в рамках нашої моделі ігрового процесу ми показали, що маючи можливість кількісної оцінки ресурсів і прогресу в досягненні ігрової мети конкретним гравцем, ми можемо проаналізувати хід його боротьби, наявність ігрової ініціативи і динаміку її зміни. Обмеження в застосуванні наший моделі розробниками може бути пов'язано з складнощами в кількісній оцінці (вимірюванні) вказаних величин. З іншого боку, стосовно комп'ютерних ігор, навіть спрощені способи вимірювань можуть виявитися корисними при розгляді логіки і принципів поведінки окремих об'єктів ігрової програми.
Задачі теорії ігор і лінійне програмування
Дата добавления: 2018-05-13; просмотров: 1016; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!