Средства MathCad для вычисления производных и интегралов
С помощь соответствующих шаблонов, расположенных на палитре Исчисления панели Математика, MathCad позволяет легко вычислять значения производных, как первого, так и высших порядков, от функции, заданной аналитическим выражением:
   
 
|
Способ вычисления определенного интеграла с использованием системы MathСad напрямую зависит от способа задания подынтегральной функции. Если подынтегральная функция задана в аналитическом виде, то интеграл может быть вычислен с помощью встроенного в систему оператора:

   
|
Если необходимо вычислить определенный интеграл от таблично заданной функции, то прямое применение встроенного оператора невозможно. Ниже приведены примеры вычисления определенных интегралов с использованием формул метода трапеций (It) и метода Симпсона (Ic).
   
 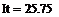
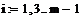 
 
|
Если подынтегральная функция задана аналитически, то может быть применен, например, метод средних прямоугольников:
    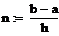 
  
|
С помощью средств MathCad можно получить символьные выражения для производных и интегралов. Символьный знак равенства (стрелка) расположен на палитре Символика панели Математика.


  
|
Средства MathCad для решения обыкновенных дифференциальных уравнений
Решением обыкновенного дифференциального уравнения (ОДУ)  является функция
является функция  , которая при всех
, которая при всех  удовлетворяет уравнению
удовлетворяет уравнению  . График решения ОДУ называется интегральной кривой. При решении ОДУ его следует привести к нормальной форме (к виду исходного ОДУ, разрешенного относительно производной)
. График решения ОДУ называется интегральной кривой. При решении ОДУ его следует привести к нормальной форме (к виду исходного ОДУ, разрешенного относительно производной) 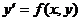
|
|
|
Для ОДУ с разделяющимися переменными исходное уравнение можно привести к виду  , тогда выражение
, тогда выражение  , задает решение
, задает решение  задачи Коши с начальными условиями
задачи Коши с начальными условиями  как функцию y от переменной х.
как функцию y от переменной х.
Например, требуется решить ОДУ вида  . Разделив переменные, получим
. Разделив переменные, получим 
Найдем частное решение данного ОДУ с использованием средств MathCad, сначала методом разделения переменных, а затем с использованием с использованием функции Odesolve(x, xk, n), где х – имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования, n – количество шагов, на которых вычисляются решение ОДУ. Результаты подтверждают правильность преобразований.
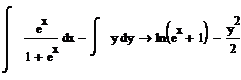  
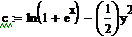  Произвольная постоянная Произвольная постоянная
 Аналитическое решение ОДУ Аналитическое решение ОДУ

    Численное решение ОДУ
Численное решение ОДУ
   
|
Аналитическое выражение для решения ОДУ удается получить достаточно редко, в таких случаях используются численные методы. Простейшими методами решения ОДУ является метод Эйлера (метод Рунге-Кутты 1-го порядка), реализуемый рекуррентной формулой вида  и модифицированный метод Эйлера (метод Рунге-Кутты 2-го порядка), имеющий рекуррентную формулу вида:
и модифицированный метод Эйлера (метод Рунге-Кутты 2-го порядка), имеющий рекуррентную формулу вида:
|
|
|

 .
.
Однако более точным является метод Рунге-Кутты 4-го порядка. Он дает погрешность решения ОДУ порядка h4. Одной из рекуррентных формул является:
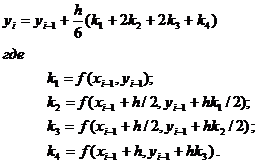
|
Решить ОДУ в пакете MathCad методами Рунге-Кутты 1-го, 2-го и 4-го порядка можно следующим образом:
   
 Метод Эйлера
Метод Эйлера
 Метод Рунге-Кутты 2-го порядка
Метод Рунге-Кутты 2-го порядка
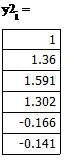
  Метод Рунге-Кутты 4-го порядка
Метод Рунге-Кутты 4-го порядка
 
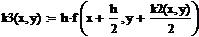 
  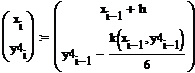 
|
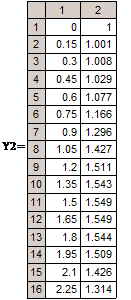
В MathCad нет средств символьного решения ОДУ, но достаточно широко представлены методы численного решения задачи Коши. Для этого предназначена, например, функция rkfixed(y, x0, xend, N, D), где y – первоначально равное y0, x0 и xend – начальное и конечное значения аргумента, N – количество проводимых вычислений решения, а переменной D(x,y) должно быть присвоено выражение для вычисления правой части уравнения. Результатом вычислений функции rkfixed служит матрица, в первом столбце которой содержатся координаты узлов x0 … xend, а во втором – значения приближенного решения в соответствующих узлах. В функции rkfixed вместо метода Рунге-Кутта используется метод Булирша-Штера. Ниже приведены решения и их графическая иллюстрация, полученные с шагом 0.6 и 0.15.

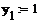 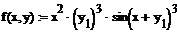  
|
Решение ОДУ 2-го порядка вида  также может быть получено методом Рунге-Кутты 4-го порядка. Ниже приведен пример решения ОДУ
также может быть получено методом Рунге-Кутты 4-го порядка. Ниже приведен пример решения ОДУ
|
|
|


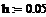 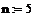






  

  
|
Дата добавления: 2018-05-12; просмотров: 630; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
