Предел функции в точке (определения). Односторонние пределы.

А. Односторонние пределы.

Определение. Число A называется левосторонним пределом функции в точке (пределом при , стремящемся к слева), если 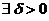: выполнено неравенство |f(x) – a|<ε. Обозначение: f(x) (или .

Аналогично дается определение правостороннего предела функции (или f(b+0)).

Пример.

B. Предел функции по Гейне

Значение называется пределом функции в точке если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов

удовлетворяющих условию выполняется неравенство .

Предел функции по Коши

Значение называется пределом функции в точке , если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов , удовлетворяющих условию , выполняется неравенство .

Окрестностное определение по Коши

Значение называется пределом функции в точке , если для любой окрестности точки существует выколотая окрестность точки такая, что образ этой окрестности лежит в .

Вопрос №11

Свойства функций, имеющих предел

Пусть определена в

Свойство №1

Пусть имеет конечный предел в точке ограничена в некоторой окрестности этой точки .

Арифметические свойства функции, имеющей предел

Свойство №2

Пусть имеют конечные пределы А и В соответственно в точке также имеют пределы в точке 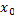, равные соответственно .

Свойство №3

Пусть определены в , и в ней выполняется и пусть .

Свойство №4(Теорема о сжатой переменной)

Пусть определены в некоторой , в ней выполняется 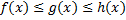и пусть .

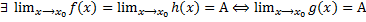Второй замечательный предел.

Доказательство второго замечательного предела:

Два случая:

1. X>0

;

Если , то .

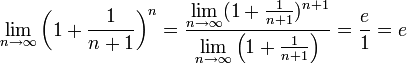
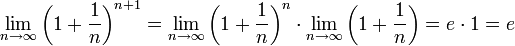, Ч.Т.Д.

2. Х<0. Пусть x= - t.

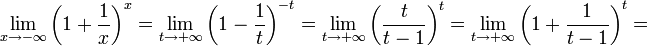
, Ч.Т.Д.

Если = t, то 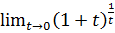= e // вторая формулировка второго замечательного предела.

Бесконечно малые и бесконечно большие функции. Свойства бесконечно малых.

Определение 1 (Бесконечно малая).
α(х) называется бесконечно малой в точке х , если lim α(х)=0, где х стремится к х
Определение 2 (Бесконечно большая).
f(х) называется бесконечно большой в точке х , если lim f(х)=∞, где х стремится к х
Свойства бесконечно малых.
Свойство 1
Алгебраическая сумма любого конечного числа бесконечно малых является бесконечно малой.
Доказательство:
Пусть α (х) …α (х) – бесконечно малые в точке х
lim(α (х) + α (х) +…+ α (х)) = 0 (х стремится к 0)
Свойство 2
Произведение бесконечно малой в точке х на ограниченную в некоторой окрестности х функцию этой точки функции f(х) является бесконечно малой.
Доказательство:
Пусть α(х) – бесконечно малая в точке х , β(х) – определена в некоторой окрестности х .

Тогда существует М >0, такое, что в некоторой окрестности этой точки выполняется неравенство │β(х)│ ≤ М
│α(х) × β(х)│ = │α(х)│ × │β(х)│ <ε/М × М = ε

< ε/М ≤ М

15. Сравнение бесконечно малых.

Отношение бесконечно малых величин образует так называемую неопределенность .

Определения

Допустим, есть бесконечно малые при одном и том же величины α(x) и β(x).

§ Если , то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

§ Если , то α — бесконечно малая высшего порядка малости, чем α. Соответственно, α = o(β).

§ Если (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости. Они эквивалентны, если с = 1.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

§ Если 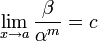(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

§ Теорема.

┘ α(х) ~ α₁(x), а β(х) ~ β₁(x) тогда

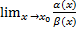
Доказательство.

= =

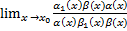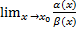
17. Свойства непрерывных в точке функций.

Функция f(x₀), определенная в окрестности некоторой точки х₀, называется непрерывной в точкех₀, если предел функции и ее значение в этой точке равны, т.е.

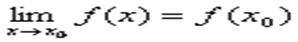
Свойства:1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.( h₁(x)=f(x) +g(x), h₂(x)=f(x)-g(x), h₃(x)=f(x)*g(x)).

Данное утверждение верно следуя теоремам:

1.Пусть функции f(x) и g(x) имеют пределы при одной и той же базе :

Тогда функция h(x)=f(x) +g(x) также имеет предел при базе , и этот предел равен сумме пределов слагаемых.

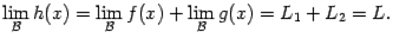
2.Пусть функции f(x и g(x) имеют пределы при одной и той же базе :

Тогда функция h(x)=f(x) +g(x) также имеет предел при базе , и этот предел равен произведению пределов сомножителей:

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

Данное утверждение верно следуя теореме:

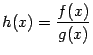Пусть при одной и той же базе существуют пределы и , причём . Тогда функция определена на некотором окончании базы , существует предел , и , то есть предел отношения равен отношению пределов числителя и знаменателя.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

Данное утверждение верно следуя следствию к теореме о произведении представленную выше:

Пусть функции имеют при базе пределы, равные соответственно , и -- постоянные. Тогда

Дата добавления: 2018-05-12; просмотров: 453; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 Следующая ⇒

Мы поможем в написании ваших работ!