Баланс энергии электромагнитного поля. Вектор Умова-Пойтинга
Лекция № 8.
Энергия электромагнитного поля
Учебные вопросы лекции:
Сторонние источники электромагнитного поля. Закон Джоуля–Ленца.
Баланс энергии электромагнитного поля. Вектор Умова-Пойнтинга.
Вектор Умова-Пойнтинга для гармонических полей.
Введение
В данной лекции рассматривается закон сохранения энергии применительно к электромагнитному полю. Физическая реальность электромагнитного поля в первую очередь проявляется в переносе энергии полем в пространстве. Непосредственное воздействие быстропеременного ЭМП на органы чувств человека вызывает ощущение тепла, а при определенной частоте колебаний – света. Однако основной научный и практический интерес представляет превращение энергии поля в иные формы, доступные наблюдению и изучению, ее виды и характер распределения в пространстве. С этой целью будет рассмотрен баланс энергии в ограниченной области пространства. В результате анализа появятся понятия потока энергии и вектора Умова-Пойнтинга, электрической и магнитной энергии.
Сторонние источники электромагнитного поля. Закон Джоуля–Ленца
В первом вопросе вводится понятие сторонних источников поля и их учет в уравнениях Максвелла, формулируются закон Джоуля-Ленца.
При рассмотрении электромагнитных процессов часто приходится иметь дело с вопросом возбуждения или создания поля (например, в теории антенн). Источник возникновения электромагнитного поля принято называть сторонней силой (или сторонним источником). Как правило, в качестве источника возбуждения электромагнитного поля выбираются токи и заряды, создаваемые каким-либо генератором, не входящим в область, где рассматривается электромагнитное поле. Между сторонними токами (зарядами) и создаваемыми ими полями имеется очевидное соответствие по частоте колебаний и в функциональной зависимости от времени.
|
|
|
Учет сторонних токов и зарядов производят путем введения их в качестве дополнительных слагаемых в выражения для плотности тока проводимости и объемной плотности заряда:
; 
, (1)
где: 
– плотность стороннего тока проводимости; rст – объемная плотность стороннего электрического заряда.
Знак "–" означает, что ток или заряд привносится из вне. С учетом (1) система уравнений Максвелла в дифференциальной форме примет вид:
(2)
Отметим, что в большинстве случаев значения 
и rст предполагаются заданными.
Определим работу, производимую электромагнитным полем при перемещении объемного заряда r в элементарном объеме ΔV на расстояние 
, где: 
– скорость перемещения заряда:
|
|
|
. (3)
Здесь 
– сила Лоренца, как показано в лекции №4. Параметром Q обозначена величина заряда внутри рассматриваемого элементарного объема ΔV. Из выражения (3) следует, что, во-первых, неподвижные заряды не могут производить работу, т.к. 
и, во-вторых, не совершает работу магнитная компонента поля, поскольку направление силы 
и направление скорости 
перемещения заряда взаимно перпендикулярны, поэтому всегда 
.
Из курса общей физики известно, что мощность связана с работой отношением: р = А/t. Следовательно, мощность, выделяемую в единице объема ΔV (которая называется также удельной мощностью), можно определить как:
. (4)
Учитывая, что вектор плотности тока проводимости 
, определим теперь полную мощность, выделяемую в объеме V:
. (5)
Полученное выражение (5) является известным законом Джоуля-Ленца в интегральной форме, а выражение (4) соответственно законом Джоуля-Ленца в дифференциальной форме.
Закон Джоуля-Ленца – физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1841 году независимо английским физиком Джеймсом Джоулем и российским физиком немецкого происхождения Эмилем Ленцом.
|
|
|
В словесной формулировке звучит следующим образом – мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля.
Если плотность тока 
обусловлена только плотностью током проводимости (как в данном случае), то мощность, определяемая по (5), является мощностью тепловых потерь, выделяемых за счет протекания тока проводимости. Другими словами, речь идет о преобразовании электромагнитной энергии в другие виды энергии.
Если же в рассматриваемой области V действуют сторонние силы, то тогда уравнение (5) с учетом выражения (1) примет вид:
. (6)
Рст – называется мощностью сторонних сил, выделяемой в объеме V, эта мощность характеризует процесс преобразования энергии различных видов (например механической, химической и др.) в электромагнитную энергию;
Рпот – мощность тепловых потерь, выделяемых за счет протекания тока проводимости.
Баланс энергии электромагнитного поля. Вектор Умова-Пойтинга
В этом вопросе формулируется закон сохранения энергии применительно к электромагнитному полю, дается физический смысл вектора Умова-Пойнтинга.
|
|
|
Выделим некоторый объем V, ограниченный поверхностью S, в котором находятся некие источники ЭМП. Поскольку закон сохранения энергии является фундаментальным законом физики, то очевидно утверждать, что энергия источников поля затрачивается на выделение тепла (или на переход в другие виды энергии), на накопление энергии ЭМП внутри объема V и на переход (излучение) энергии из этого объема в прилегающее к нему пространство, то есть:
Рст = Рпот + Рзап + Рпер (7)
где: Рст – мощность, выделяемая сторонними источниками; Рпот – мощность тепловых потерь; Рзап – мощность, затрачиваемая на накопление энергии ЭМП (запасаемая мощность); Рпер – мощность, выходящая из рассматриваемого объема.
Определим конкретные значения составляющих выражения (7). Возьмем 1-ое и 2-ое уравнения Максвелла в дифференциальной форме с учетом сторонних сил и помножим 1-ое уравнение на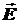 
, а 2-ое уравнение на вектор 
:
(8 а)
(8 б)
Далее вычтем из (8 б) выражение (8 а) в результате получим:
.
Преобразуем левую часть полученного выражения, используя известное тождество из векторного анализа,
,
где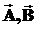 
- произвольные векторы; 
- обозначает векторное произведение.
В результате получим, что дивергенция скалярного произведения векторов напряженности электрического и магнитного поля равна:
. (9)
Проинтегрируем данное выражение по объему V, ограниченному замкнутой поверхностью:
.
Применив к левой части полученного уравнения теорему Остроградского – Гаусса, получим:
.
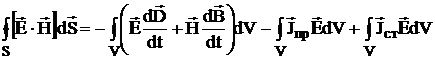Перегруппируем данное выражение, оставив в правой части лишь составляющую, содержащую плотность тока сторонних сил, тогда окончательно:
. (10)
Полученное уравнение (10) называют теоремой Умова-Пойтинга в интегральной форме. Оно характеризует баланс энергии электромагнитного поля в замкнутом объеме V, ограниченном поверхностью S.
Выясним физический смысл отдельных членов, входящих в выражение (10).
1) Физический смысл интеграла 
ясен из выражения (6). Он характеризует мощность сторонних сил, которая выделяется в рассматриваемом объеме V.
2) Выражение 
характеризует мощность тепловых потерь в рассматриваемом объеме V, создаваемых за счет протекания тока проводимости.
3) Для выяснения физического смысла выражения 
рассмотрим особый случай:
– пусть сторонние источники в объеме V отсутствуют, тогда Рст = 0;
– кроме того, пусть граница S непроницаема для электромагнитного поля (т.е. является идеально проводящей), тогда, поскольку поле на границе S отсутствует ( 
и 
), то 
.
В этом случае, получаем:
.
Отсюда делаем первый вывод: рассматриваемый интеграл характеризует некую мощность в объеме V. Далее, поскольку область V не сообщается с внешней средой (S - непроницаема), то отсюда следует, что рассматриваемый интеграл будет характеризовать мощность, запасенную в объеме V. Так как в нашем случае эта мощность расходуется на потери (нагрев среды) то, очевидно, запасенная мощность Рзап должна убывать. Этому как раз и соответствует знак «–».
Из курса общей физики известно, что мощность связана с энергией как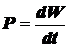 
, тогда:
.
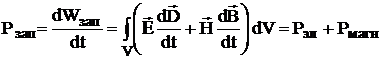Вывод: Рассматриваемый интеграл характеризует скорость изменения электромагнитной энергии, сосредоточенной внутри области V, другими словами мощность, запасенную в этой области. Интеграл 
характеризует мощность электрического поля, сосредоточенную в объеме V, а интеграл 
характеризует соответственно мощность магнитного поля, сосредоточенную в этом же объеме.
4) Для выяснения физического смысла интеграла 
также рассмотрим особый случай:
– пусть отсутствуют потери на нагрев среды, т.е. Рпот = 0;
– электромагнитная энергия внутри области V остается постоянной, следовательно, dW/dt = 0.
В этом случае получаем:
.
Отсюда можно сделать первый вывод: рассматриваемый интеграл есть мощность, кроме того, поскольку данный интеграл берется по замкнутой поверхности S, то это мощность, проходящая через поверхность S. Так как потери отсутствуют, а запасенная энергия постоянна в данном объеме (Wзап = const), то мощность сторонних сил расходуется на излучение электромагнитной энергии из рассматриваемого объема V. Следовательно, в данном случае интеграл характеризует мощность излучения Ризл.
В случае, когда Рст = 0 , W = const, получаем: 
, и в данном случае рассматриваемый интеграл характеризует мощность, которая входит через поверхность S (обратите внимание на знак «–») в объем V и расходуется там в виде потерь.
Вывод: Рассматриваемый интеграл характеризует мощность, которая в зависимости от знака, либо выходит («+»), либо входит («–») через поверхность S, рассматриваемого объема V. Таким образом, этот интеграл характеризует мощность перехода между выделенным объемом и внешним, по отношению к этому объему, пространством.
Векторное произведение 
составляющих электромагнитного поля называют вектором Умова-Пойнтинга 
.
Определим единицу измерения вектора Умова-Пойнтинга. Поскольку измеряется в В/м, а 
- в А/м, то очевидно, что для единицей измерения является В×А/м2 = Вт/м2 . Таким образом, вектор Умова-Пойнтинга характеризует мгновенное значение плотности мощности, проходящей через замкнутую произвольную поверхность S в один квадратный метр, параллельную плоскости, в которой расположены векторы и .
Исходя и вышеизложенного, запишем уравнение баланса электромагнитного поля, которое также носит название закона сохранения электромагнитной энергии:
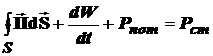. (11)
В заключение этого вопроса рассмотрим два частных примера, изображенных на рис. 1.
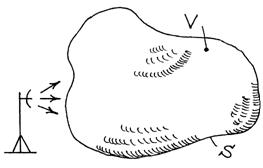
а) б)
Рис. 1 – Примеры для выяснения смысла уравнения баланса ЭМП
Запишем уравнение баланса электромагнитного поля для этих примеров. Для случая на рис. 1 а, когда рассматривается объем, в котором присутствуют сторонние силы (эту роль выполняет передающая антенна), уравнение баланса принимает вид:
Рст = Рпот + Рзап + Ризл =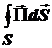 
.
Для случая на рис. 1 б, когда рассматривается объем, в котором отсутствуют сторонние силы, очевидно, что уравнение баланса будет иметь вид:
Рпот + Рзап = – Рприем = .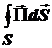
Мощность излучения Ризл или мощность приема Рприем являются мощностью перехода, т.е. мощностью, проходящую через замкнутую поверхность S рассматриваемого объема V.
Вывод:Конкретный вид уравнения баланса определяется рассматриваемой областью V при заданных источниках сторонних сил.
Дата добавления: 2018-05-12; просмотров: 3527; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!