ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ КАСАТЕЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Лекция № 7. Граничные условия на поверхности раздела сред

 

Учебные вопросы лекции:

Граничные условия для нормальных составляющих векторов электромагнитного поля.

Граничные условия для касательных составляющих векторов электромагнитного поля.

Граничные условия на поверхности идеального диэлектрика и идеального проводника.

Введение

 

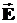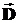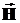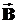При решении практических задач электродинамики помимо уравнений Максвелла необходимо также знать граничные условия, т.е. знать соотношения между векторами поля в двух очень близких точках, находящихся по обе стороны границы раздела сред. Если на границе между различными материальными средами параметры среды e, m, s скачкообразно изменяются, то, очевидно, векторные функции , ,  и  будут иметь разрывы. Определить характер этих разрывов и означает задать граничные условия на поверхности раздела сред. Поскольку разрывные функции нельзя дифференцировать, то для нахождения соотношения поля на границе раздела, необходимо использовать интегральные уравнения Максвелла и предельные переходы.

 

 

ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ НОРМАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

 

 

В первом вопросе формулируется закон поведения нормальных составляющих векторов поля на границе раздела двух сред.

Рассмотрим плоскую границу раздела двух сред с параметрамиe_a1, m_a1, s₁ и e_a2, m_a2, s_2. На поверхности раздела сред выделим достаточно малый элемент DS , в пределах которого в обеих средах нормальные составляющие вектора  равномерно распределены. На основании DS построим цилиндр с высотой h так, чтобы его основания находились в разных средах, как показано на рис. 1.

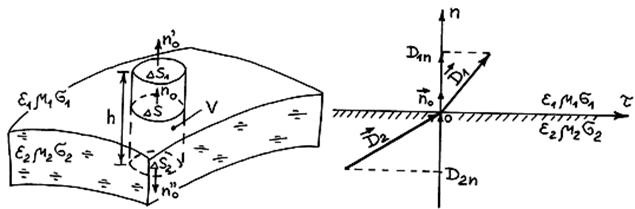
Рис. 1 – Пояснение к выводу граничных условий для нормальных составляющих электрического поля

 

Используем 3-е уравнение Максвелла в интегральной форме, согласно которому поток вектора электрической индукции через любую замкнутую поверхность S равна сумме зарядов в объеме V, ограниченном этой поверхностью, т.е.:

                                          ,

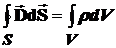где: 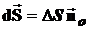– единичный вектор, нормальный к малой площадке 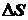; 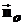– нормаль к 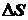, r - объемная плотность электрического заряда.

Разобьем интеграл по замкнутой поверхности S, ограничивающий объем V, на три интеграла:

              .

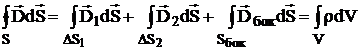Устремим высоту цилиндра h к нулю, тогда: основания цилиндра устремляются к площади круга на границе раздела двух сред, а площадь боковой поверхности воображаемого цилиндра к нулю, т.е.

    ΔS₁ и ΔS₂ ® ΔS;              S_бок = h×DS ® 0; ;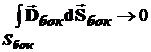

тогда интеграл по объему V будет стремиться к интегралу по элементарной площади:                            ,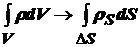

где: r_S – поверхностная плотность заряда на границе раздела сред.

Учитывая это, получаем: .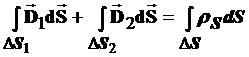

Определим теперь нормальные составляющие вектора 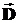. Из рис. 1 очевидно, что:

.

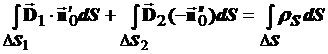Наконец, считая площадку ΔS настолько малой, что на этой площади вектор 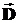 практически не изменяется, получим:

.

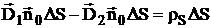Окончательно: 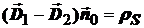, или

D_1n – D_2n = r_S.                              (1)

Итак, делаем вывод: нормальная составляющая вектора электрической индукции при переходе через граничную поверхность претерпевает скачок, численно равный поверхностной плотности электрического заряда.

Поскольку из материальных уравнений 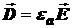 то, следовательно, граничные условия для нормальной составляющей вектора напряженности электрического поля будут иметь вид:

e_а1Е_1n - e_а2Е_2n = r_S .                    (2)

Если граничная поверхность не заряжена, то нормальнаякомпонента D_n вектора электрической индукции на основании (1) непрерывна при переходе из среды 1 в среду 2, а нормальная компонента E_n вектора напряженности электрического поля терпит разрыв, величина которого определяется соотношением диэлектрических проницаемостей сред:

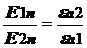(при r_S = 0).

 

Рассмотрим теперь граничные условия для нормальных составляющих магнитного поля. Для этого по аналогии охватим обе среды цилиндром с объемом V и используем 4-ое уравнение Максвелла в интегральной форме, согласно которому поток вектора магнитной индукции В через любую замкнутую поверхность S равен нулю:

.

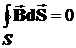Разобьём замкнутый интеграл по поверхности на три интеграла:

.

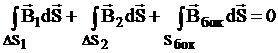Устремим высоту цилиндра  h ® 0 тогда:

.

Наконец, учитывая постоянство 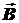 на площадке  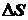из-за малости последней, получим для нормальных составляющих:

,

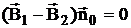или                        B_1n – B_2n = 0.                                          (3)

В результате делаем вывод о том, что нормальная составляющая вектора магнитной индукции при переходе через границу раздела двух сред остается непрерывной.

Поскольку из материальных уравнений 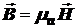  то, граничные условия для нормальных составляющих вектора напряженности магнитного поля имеют вид:

m_а1Н_1n = m_а2Н_2n .                                    (4)

 

Таким образом, нормальная составляющая вектора 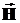 на границе сред терпит разрыв, величина которого равна отношению абсолютных магнитных проницаемостей сред.

.

 

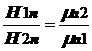ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ КАСАТЕЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

 

В этом вопросе формулируется закон поведения касательных составляющих векторов поля на границе раздела двух сред.

Рассмотрим плоскую границу раздела двух сред с параметрами e_а1, m_а1, s₁ и e_а2, m_а2, s₂. Охватим обе среды элементарным контуром L, плоскость которого перпендикулярна поверхности раздела двух сред (см. рис. 2).

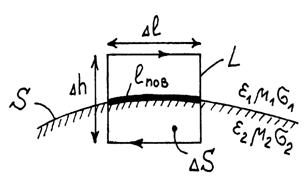
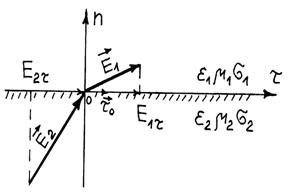
Рис. 2 –Пояснение к выводу граничных условий для касательных составляющих электрического поля

 

Используем 2-ое уравнение Максвелла в интегральной форме, согласно которому циркуляция вектора напряженности электрического поля Е (т.е. ЭДС) по любому замкнутому контуру L равна скорости изменения магнитного потока, пронизывающего этот контур с обратным знаком:

.

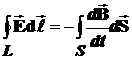Разобьем контур L на четыре участка, два из которых определяются вектором элементарной длины 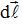, а два других – вектором элементарной высоты  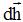, тогда интеграл по замкнутой кривой можно разбить на четыре линейных интеграла:

.

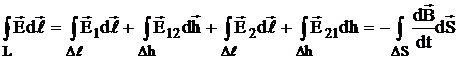Устремим высоту контура Δh к нулю, тогда элементарная площадь, ограниченная контуром, ΔS = Δl ^.Δh в пределе будет стремится к нулю, а стороны АВ и CD сливаются на границе, и в этом случае получаем:

.

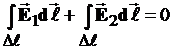Определим касательные составляющие вектора напряженности электрического поля:

,

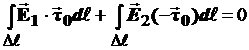где 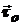  - единичный касательный вектор.

Наконец, полагая, что отрезок Δl настолько мал, что вектор 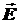  на данном участке не изменяется, получим:

.

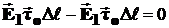Окончательно: , или

                               Е_1t = Е_{2t .}                                       (5)

 

Таким образом, касательная составляющая вектора напряженности электрического поля непрерывна на границе раздела сред.

Используя материальное уравнение 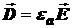 определяем:

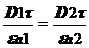.                                                   (6)

В результате делаем вывод о том, что касательные составляющие вектора 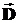 терпят разрыв, величина которого определяется соотношением диэлектрических проницаемостей обеих сред.

.

 

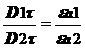Рассмотрим граничные условия для касательных составляющих вектора напряженности магнитного поля 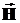. По аналогии с предыдущим случаем, охватим границу раздела сред контуром L и используем 1-ое уравнение Максвелла. Согласно которому циркуляция вектора напряженности магнитного поля Н по любому замкнутому контуру L равна сумме электрического тока проводимости и тока смещения, протекающих сквозь поверхность, ограниченную этим контуром:

.

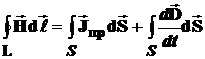Разбиваем интеграл по замкнутому контуру L на 4-ре интеграла:

.

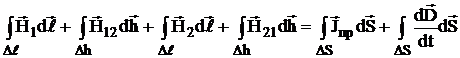Устремим высоту контура Δh к нулю, тогда элементарная площадь, ограниченная контуром, ΔS = Δl^.Δh в пределе будет стремится к нулю, а интегралы:

, , , ,

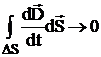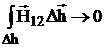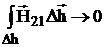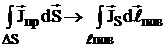где: 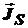 - вектор плотности поверхностного тока проводимости, пересекающий отрезок линии l_пов (см. рис. 3.).

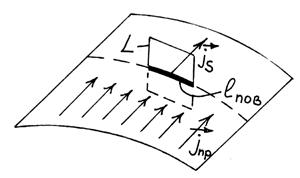
Рис. 3- Понятие вектора плотности поверхностного тока проводимости

 

Следовательно, получаем:

.

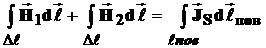Наконец, учитывая постоянство 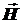 на площадке 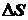, получим для касательных составляющих:

,

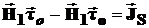или:                                           Н_1t  – Н_2t = J_S.                                   (7)

Итак, делаем вывод о том, что касательная составляющая вектора напряженности магнитного поля на границе раздела сред претерпевает скачок, численно равный поверхностной плотности тока проводимости, протекающего по границе раздела сред.

Используя материальное уравнение 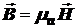, определим граничные условия для касательных составляющих вектора магнитной индукции:

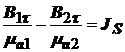.                                           (8)

Если по граничной поверхности ток не протекает, т.е. 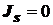, то касательная компонента H_t вектора напряженности магнитногополя на основании (7) непрерывна при переходе из среды 1 в среду 2, а нормальная компонента B_t вектора магнитной индукции терпит разрыв, величина которого определяется соотношением магнитных  проницаемостей сред:

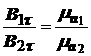(при J_S = 0).

 

---

Дата добавления: 2018-05-12; просмотров: 2163; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!