Круглый и коаксиальный объемные резонаторы

Стр 1 из 3Следующая ⇒

Лекция № 15.

Объемные резонаторы

Учебные вопросы лекции:

Общие свойства объемных резонаторов. Прямоугольный объемный резонатор. Условие резонанса.

Круглый и коаксиальный объемные резонаторы.

Возбуждение объемного резонатора и его эквивалентная схема. Способы включения объемного резонатора в линию передачи.

Собственная, нагруженная и внешняя добротности объемного резонатора.

Введение

Создание обычных LС колебательных контуров на высоких частотах становится весьма проблематичным в связи с резким возрастанием потерь и излучением во внешнее пространство. Такой контур с сосредоточенными элементами L и С становится неспособным к накоплению электромагнитной энергии, и его резонансные свойства существенно ухудшаются. Поэтому в диапазоне дециметровых и сантиметровых волн применение нашли колебательные контуры в виде замкнутых металлических полостей, в которых электромагнитные колебания возникают внутри ограниченного объема, что и дало название данным резонаторам – объемные. Впервые объемные резонаторы теоретически и практически исследовались М.С. Нейманом (1937 г.). В отличие от колебательного контура с сосредоточенными LС элементами в объемном резонаторе электрические и магнитные поля не разделены в пространстве. В связи с этим электромагнитные процессы в нем должны описываться уравнениями Максвелла, а не уравнениями электрических цепей. Поэтому анализ основных типов объемных резонаторов в этом разделе проводится на основании уравнений электромагнитного поля.

Цель данной лекции является изучение объемных резонаторов.

Общие свойства объемных резонаторов. Прямоугольный объемный резонатор. Условие резонанса

В первом вопросе лекции рассматриваются причины невозможности использования обычных LС контуров на СВЧ, дается представление объемного резонатора в виде колебательной системы с распределенными параметрами, исследуется характер поведения электромагнитного поля в прямоугольном резонаторе. Определяется условие существования собственных частот прямоугольного резонатора.

Объемным резонатором называется электромагнитная колебательная система, представляющая собой замкнутый объем с проводящими стенками.

На низких частотах, в качестве колебательного контура (резонатора) широко применяется параллельное соединение из сосредоточенной индуктивности L и емкости C (см. рис. 1). Известно, что резонансная частота такого контура определяется как:

. (1)

Рис. 1 – Колебательный контур на НЧ

Колебательный процесс в такой системе (см. рис. 1) возникает, как известно, в результате обмена энергией между электрическим полем, сосредоточенным в индуктивности и магнитным полем, сосредоточенным в индуктивности

Чтобы организовать резонатор на СВЧ необходимо, как следует из формулы (1), уменьшатьL и С. Однако, с уменьшением L и С, соответственно уменьшается энергия, запасаемая в L и С, и, кроме того, с увеличением w происходит рост тепловых потерь (характеризуемое сопротивлением R) в контуре. К этому следует добавить, что на СВЧ обычный колебательный контур по размерам становится соизмеримым с длиной волны, а это, как было показано в разделе "Излучение электромагнитных волн", приводит к тому, что резонансный контур сильно излучает в окружающее пространство Следовательно, в СВЧ диапазоне создание колебательных контуров из сосредоточенных элементов L и C с большой добротностью становится практически невозможным.

Поэтому необходимо строить колебательные контуры на СВЧ на иной основе. То, что это возможно, следует из первого и второго уравнений Максвелла:

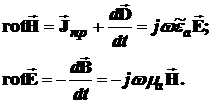
Согласно этим уравнениям переменное электрическое поле является источником переменного магнитного поля, которое, в свою очередь, возбуждает переменное электрическое поле и т.д., то есть происходит непрерывный обмен энергиями между электрическими и магнитными полями. Если теперь каким-либо образом устранить излучение электромагнитных волн в некоторой области и добиться отсутствия тепловых потерь, то обмен энергиями должен протекать сколь угодно долго. А это и является ни чем иным, как незатухающим колебательным процессом.

Поэтому простейшими резонаторами на СВЧ являются некоторые объемы, ограниченные со всех сторон металлическими поверхностями, предотвращающими излучение электромагнитного поля во внешнее пространство. По аналогии с направляющими системами принято различать: прямоугольный, круглый и коаксиальный резонаторы (см. рис. 2). Кроме этих резонаторов, на СВЧ широко используются тороидальные и сферические резонаторы. Можно осуществить и более сложные по конструкции резонаторы, например диэлектрические, спиральные, ферритовые и т.д. Подобные резонаторы находят применение в функциональных СВЧ устройствах и в квантовой электронике.

Рисунок 8.2- Типичные резонаторы, используемые на СВЧ

На низких частотах основными параметрами резонаторов являются L, C и R. Все прочие вторичные параметры (резонансная частота w₀, добротность Q и т.д.) выражаются через эти величины.

На СВЧ параметры L, C и R не имеют реального физического эквивалента, поскольку их нельзя непосредственно измерить. Поэтому на СВЧ в качестве основных параметров фигурируют:

- l₀ – резонансная длина волны;

- Q₀ – собственная добротность;

- G – активная проводимость, характеризующая потери в резонаторе.

По этим параметрам затем определяют эквивалентные значения L, C и R колебательного контура, строится его эквивалентная схема, на основе которой возможно проводить инженерный расчет резонансных цепей.

Рассмотрим отрезок прямоугольного волновода сечением a ´ b, ограниченного торцевыми металлическими поверхностями, расположенными в сечениях z = 0 и z = l (см. рис. 3).

Рис. 3 – Прямоугольный резонатор

Рассмотрим сначала частный случай, когда по волноводу может распространяться только волна Н₁₀ вдоль направления z. Условно будем называть эту волну падающей. Напряженность электрического поля для этой падающей волны определяется уравнением

.

Наличие торцевых поверхностей приводит к тому, что в образовавшемся объеме возникает также и отраженная волна:

.

Результирующее электрическое поле получается так:

Накладываем граничные условия: касательная составляющая электрического поля на торцевых стенках должна быть равна нулю, т.е. Е_y_S = 0 при z = 0 и z = l.

При z = 0 имеем:

Чтобы это условие выполнялось при любом x, необходимо потребовать, чтобы А = –1.

При z = l имеем:

Чтобы это условие выполнялось при любом х, необходимо, чтобы: или , где p =1, 2, 3…

отсюда: .

Таким образом, результирующее электрическое поле в прямоугольном резонаторе выражается как:

, (2)

причем b должно принимать строго фиксированные значения:

. (3)

На основании (2) и (3) можно сформулировать следующие выводы:

1) Полученное результирующее поле не распространяется вдоль оси z (поскольку отсутствует множество ). Колебаниям данного поля соответствует стоячая волна, существующая как по оси х, так и по оси z.

2) Электрическое результирующее поле может существоватьне при любом значении постоянной распространенияb, а только если оно отвечает условию (3). Данное условие получило названия условия резонанса прямоугольного резонатора.

Поскольку , где: l_В – длина волны в прямоугольном волноводе, то, следовательно, резонансная длина волны в волноводе прямоугольного резонатора может быть определена из условия:

. (4)

Получим теперь выражение для магнитного поля в прямоугольном резонаторе, используя второе уравнение Максвелла:

здесь m_а – вещественная величина (предполагается, что магнитные потери отсутствуют).

Раскрывая операцию rot и учитывая, что для волны Н₁₀ составляющие Н_y= E_x= E_z= 0, получим:

(5)

Проанализируем полученные выражения для векторов электрического (2) и магнитного (5) полей:

1) Между Е и Н составляющими постоянно существует сдвиг фаз по времени на величину , что является следствием непрерывного обмена энергиями между электрическим и магнитным полями.

2) Мгновенное значение вектора Пойнтинга получается равным:

Отсюда видно, что среднее значение вектора Пойнтинга за период колебания равно нулю. Это означает, что объемный резонатор с энергетической точки зрения подобен обычному колебательному контуру.

Рассмотрим теперь более общий случай, когда в прямоугольном волноводе может распространяться любая из волн Е_mn– или Н_mn–типа. Поскольку постоянная распространения для любого типа волны определяется как , или:

, (6)

то, учитывая условие резонанса (3) , находим:

Критическая длина волны прямоугольного волновода определяется с помощью выражения:

Зная l_Врез и l_кр_mn , определим с помощью (8.6) собственную резонансную длину волны прямоугольного резонатора для волн H_mn– и E_mn–типа:

, (7)

и собственную частоту, равную:

, (8)

где: u – скорость распространения электромагнитных волн в диэлектрике, заполняющем резонатор.

Каждой тройке чисел m, n и p соответствует своя определенная резонансная частота и своя структура поля, которая соответствует типу колебания в прямоугольном резонаторе, обозначаемому как: E_mnp – для электрических волн; H_mnp – для магнитных волн.

Структура полей для некоторых типов колебаний прямоугольного резонатора изображена на рис. 4.

Как следует из (8), объемный резонатор, как колебательный контур на СВЧ, может иметь бесконечное множество собственных резонансных частот, тогда как одиночный колебательный контур на НЧ имеет единственную резонансную частоту.

Рис. 4 – Структура поля колебаний Н₁₀₁ и Н₁₀₂ в прямоугольном резонаторе

Круглый и коаксиальный объемные резонаторы

В этом вопросе определяется условие существования собственных частот круглого и коаксиального резонаторов.

Рассмотрим отрезок круглого волновода, ограниченного с обеих сторон металлическими поверхностями (рис. 5). Поставим задачу нахождения всей совокупности резонансных частот данного круглого резонатора.

Рис. 5 – Круглый резонатор

Внутри круглого волновода, как известно, могут распространяться волны E_mn– и H_mn–типа. Независимо от типа волны постоянная распространения в круглом волноводе определяется как:

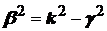(9)

где: , l_В – постоянная распространения и длина волны в круглом волноводе; , l – постоянная распространения и длина волны в неограниченном пространстве; - поперечное волновое число; l_крn_m – критическая длина волны колебания с индексами m и n.

Критические длины волны для колебаний E_mn и H_mn определяются как:

; ;

где: V_n_m – m-ый корень функции Бесселя n-го порядка, U_n_m – m-ый корень производной функции Бесселя n-го порядка.

Условием резонанса круглого резонатора, также как и для прямоугольного резонатора, является: , где: p=1, 2, 3…

отсюда:

Пользуясь (8.9), определим собственные резонансные длины волн для любого типа колебаний в круглом резонаторе:

, или:

Отсюда:

; . (10)

Каждой тройке чисел n, m и p соответствует своя, строго определенная резонансная частота и своя структура поля, которая соответствует типу колебания в круглом резонаторе, обозначаемому как: Е_mnp – для электрических волн и Н_mnp – для магнитных волн. Структура полей для некоторых типов колебаний круглого резонатора изображена на рис. 6.

Рис. 6 – Структура полей колебаний Е₀₁₀ и Е₁₁₁ в круглом резонаторе

Рассмотрим теперь отрезок коаксиального волновода, закороченного с обеих сторон металлическими поверхностями (см. рис. 7).

Рис. 7 – Коаксиальный резонатор

Определим резонансные длины волн данного резонатора при условии, что в коаксиальном волноводе распространяется ТЕМ – волна. Для ТЕМ – волн в коаксиальном волноводе: g² = k² - b² = 0, или k = b.

Используя условие резонанса , где: р = 1, 2, 3, …, определим собственные резонансные длины волн в коаксиальном резонаторе:

Откуда: . (11)

Наибольший практический интерес представляют колебания ТЕМ–волны в коаксиальном резонаторе с индексом р = 1. В этом случае вдоль резонатора укладывается одна полуволна поля. Картина поля колебаний типа ТЕМ₁ в коаксиальном резонаторе представлена на рис. 8.

Рис. 8 – Структура поля колебания ТЕМ₁ в коаксиальном волноводе

Исходя из (11), собственная резонансная частота колебания ТЕМ₁ выражается как:

где: e и m – электромагнитные параметры диэлектрика, заполняющего резонатор.

Как следует из этого выражения, собственная частота, соответствующая колебаниям типа ТЕМ₁, не зависит от отношения диаметров d/D и определяется только длиной резонатора.

Дата добавления: 2018-05-12; просмотров: 3835; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!