Использование круглых волноводов в качестве линии передачи

Стр 1 из 2Следующая ⇒

Лекция № 14.

Направляемые электромагнитные волны в круглом и коаксиальном волноводах

Учебные вопросы лекции:

Круглый волновод.

Использование круглых волноводов в качестве линии передачи.

Коаксиальный волновод.

Основные характеристики ТЕМ–волны в коаксиальном волноводе.

Введение

В радиотехнической практике особое значение приобретает задача направленной передачи энергии электромагнитных волн от генератора к потребителю. В качестве основных требований, которые при этом предъявляются, выступают минимум потерь при передаче и максимум передаваемой мощности. Поставленная задача решается с помощью специальных направляющих устройств, носящих название линий передачи. В данном разделе будет рассмотрено несколько типов линий передачи, используемых в диапазоне частот 30 МГц – 30 ГГц, и будут исследованы механизмы распространения в них электромагнитных волн. Основное внимание уделено линиям передачи в виде полых металлических труб, различного поперечного сечения (волноводам) и коаксиальным линиям передачи.

Цель данной лекции является изучение направляемых электромагнитных волн в круглом и коаксиальном волноводах.

Круглый волновод

В первом вопросе лекции рассматривается решение уравнений Максвелла применительно к полым волноводам круглого сечения, изучаются основные свойства и структура направляемых волн в круглом волноводе.

Полая металлическая труба круглого поперечного сечения называется круглым волноводом. Обозначим радиус круглого волновода через R (см. рис. 1). Будем полагать, что волновод заполнен однородной изотропной средой без потерь (s » 0). Сторонние токи отсутствуют.

Рис. 1 – Круглый волновод

В этом случае 1-ое и 2-ое уравнения Максвелла примут вид:

Для круглого волновода удобнее ввести цилиндрическую систему координат (r, j, z) и искать решение данных уравнений в этой системе координат. Порядок решения уравнений аналогичен тому, как в случае прямоугольного волновода:

1) Раскрывается операция rot в цилиндрической системе координат.

2) Все поперечные составляющие поля (т.е. Е_r, Е_j, Н_r, Н_j) выражаются через продольные Е_z и Н_z.

3) Составляется дифференциальное уравнение для продольных составляющих и находится его решение.

Как и в прямоугольном волноводе, в круглом волноводе могут существовать как Е, так и Н – волны. Рассмотрим сначала Е – волны. По определению, для таких волн: Н_z = 0, все остальные составляющие не равны 0.

Составим дифференциальное уравнение для амплитудного значения продольной составляющей Е_z_m:

где: g² = k² - b² – поперечное волновое число; k – постоянная распространения волны в неограниченном (свободном) пространстве; b - постоянная распространения волны в круглом волноводе; Ñ² – поперечный оператор Лапласа.

Раскрывая Ñ² в цилиндрической системе координат, получим:

Решая это дифференциальное уравнение методом разделения переменных, получим:

где: Е₀ – некоторая постоянная; J_n – функция Бесселя n – го порядка, n=0,1,2,…

Теперь накладываем граничные условия: касательная составляющая электрического поля должна быть равна 0 на стенках волновода, т.е. Е_j = 0 при r = R. Это означает, что и Е_z_m должна быть равна нулю при r = R, т.е:

Чтобы данное требование выполнялось при любом угле j, необходимо, чтобы выполнялось условие:

J_n(gR) = 0. (1 а)

Функции Бесселя различного порядка изображены на графике рис. 2.

Рис. 2 – Функции Бесселя

Из графиков видно, что для выполнения условие (1 а) необходимо, чтобы:

gR = V_nm , (1 б)

где: V_nm – m – ый корень функции Бесселя n – го порядка.

Из (1 б) получаем, что поперечное волновое число:

Следовательно, амплитудное значение продольной составляющей:

а мгновенное значение:

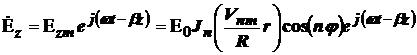. (2)

При известной Е_z, далее определяются все остальные составляющие поля Е – волны: E_z, E_φ, H_r, H_φ.

Проведем анализ полученного уравнения (2).

1) Направляемая волна Е – типа распространяется по круглому волноводу вдоль оси z с постоянной распространения β. Каждой паре чисел m и n соответствует своя структура электромагнитного поля, которая обозначается как Е_nm. Из графиков на рис. 2 видно, что наименьшим корнем функции Бесселя является корень V₀₁, следовательно простейшей волной Е – типа является волна Е₀₁.

2) Определим постоянную распространения β для Е_nm волн.

Поскольку:

то отсюда:

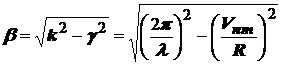Аналогично, как и для прямоугольного волновода получаем:

- если k²> γ², то β – вещественная величина и, следовательно, электромагнитная волна Е_nm будет распространяется в круглом волноводе;

- если k²< γ², то β – мнимая величина, поэтому электромагнитный процесс будет экспоненциально затухать вдоль круглого волновода;

- граничный случай возникает когда:

k² = γ² или .

Длина волны, отвечающая этому условию, называется критической длиной волны в круглом волноводе:

Определим длину волны в круглом волноводе.

Поскольку 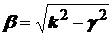, или: , то:

. (3)

Заметим, что выражение (3) имеет тот же вид, что и для прямоугольного волновода.

Определим фазовую V_ф и групповую V_гр скорости Е – волны в круглом волноводе:

Так как V_ф× V_гр= с², то:

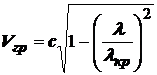Рассмотрим теперь Н – волны в круглом волноводе. Для этих волн по определению составляющая Е_z=0, все остальные составляющие не равны нулю. Составим дифференциальное уравнение для амплитудного значения продольной составляющей Н_z_m:

Решение этого уравнения имеет вид:

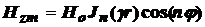Накладываем граничные условия: Е_φ= 0 при r = R. Это означает, что производная составляющей H_zm при r = R должна быть равна нулю, т.е:

Для выполнения данного условия при любом j, необходимо чтобы:

J_n¢(gR)=0. (4)

Первая производная любой функции – это есть точки максимума или минимума этой функции. Поэтому (см. рис. 2), чтобы выполнялось условие (4), необходимо потребовать:

gR=U_nm , (5)

где: U_nm – m-ый корень производной функции Бесселя n-го порядка.

Следовательно, из (5) волновое число g для Н – волн в круглом волноводе:

.

Тогда мгновенное значение продольной составляющей Н_z равно:

.

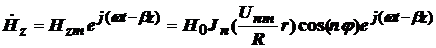Анализ полученного уравнения показывает, что каждой паре чисел m и n соответствует своя структура поля Н – волны в круглом волноводе, которая обозначается как Н_mn. Из графиков на рис. 2 видно, что первым корнем является корень U₁₁, Поэтому простейшей волной Н – типа будет волна Н₁₁.

Критическая длина волны Н – типа определяется из условия: k²=g².

Или , отсюда: .

Поскольку корень U₁₁ является наименьшим из всех возможных корней функции Бесселя, то l_кр волны Н₁₁ будет наибольшей из всех Н_nm и Е_nm типов волн. Это означает, что одномодовый режим работы круглого волновода возможен только на волне Н₁₁. Вывод формул для l_в, V_ф, и V_гр аналогичен тому, как это проводилось для Е – волн и не представляется сложным при самостоятельном изучении.

Использование круглых волноводов в качестве линии передачи

В этом вопросе рассматриваются особенности применения круглых волноводов в качестве линий передачи СВЧ мощности.

В круглом волноводе, в отличие от прямоугольного волновода, в качестве основного типа колебания, используется один из трех типов волн: Н₁₁, Е₀₁ или Н₀₁. Рассмотрим особенности этих волн, обусловливающих их применение на практике.

а) Обратимся к структуре электромагнитных волн этих волн, изображенных на рис. 3, и распределению линий поверхностного тока, показанных на рис. 4. Отметим, что у волны Н₀₁ в отличии от волн Н₁₁ и Е₀₁ отсутствует продольная составляющая тока проводимости (существуют только поперечные, кольцевые токи).

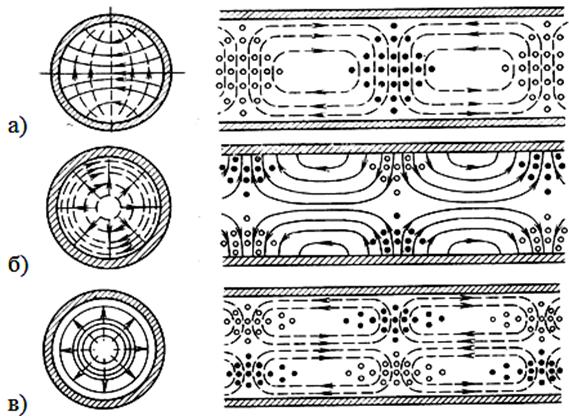
Рис. 3 – Структура волн Н₁₁ (а), Е₀₁(б) и Н₀₁ (в) в круглом волноводе

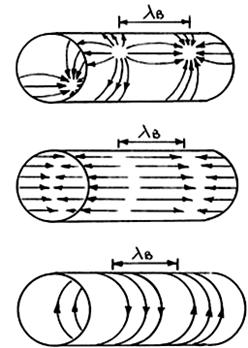
Рис. 4 – Распределение линий поверхностного тока для волн Н₁₁ (а), Е₀₁(б) и Н₀₁ (в)

б) Критическая длина волны для колебаний Е– и Н–типа в круглом волноводе определяется выражениями:

где: R – радиус круглого волновода; V_nm – m-ый корень функции Бесселя n-го рода; U_nm – m-ый корень производной функции Бесселя n-го рода.

В табл. 1 приведены значения l_кр первых шести типов колебаний в круглом волноводе.

Таблица 7.1

Тип волны	Н₁₁	Е₀₁	Н₂₁	Е₁₁	Н₁₁	Н₃₁
l_кр/R	3,42	2,61	2,06	1,64	1,64	1,46

На рис. 5 приведены зависимости коэффициента затухания a в круглом волноводе от частоты и допустимой мощности Р от частоты для рассматриваемых трех типов волн.

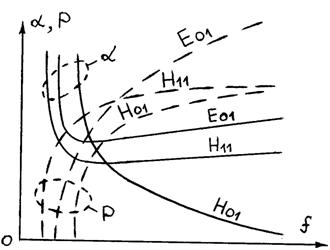
Рис. 5 – Зависимость a и Р от частоты

На основании рис. 3, 4, 5 и табл. 1 несложно сформулировать следующие особенности волн Н₁₁, Е₀₁ и Н₀₁:

Волна Н₁₁

1) Данный тип колебаний обладает наибольшей l_кр. Следовательно, только на волне Н₁₁ возможен одномодовый режим работы круглого волновода без применения каких-либо дополнительных мер;

2) Структура электромагнитного поля данной волны является несимметричной относительно произвольной поперечной оси (см. рис. 3). Вследствие этого, при движении волны вдоль круглого волновода происходит изменение поляризации волны, как показано на рис. 6.

3) Чтобы зафиксировать плоскость поляризации, на практике прибегают к изменению поперечного сечения круглого волновода, используя эллипс, и переходя таким образом к эллиптическим волноводам (см. рис. 7);

4) Из всех трех типов волн, волна Н₁₁ обладает наибольшей допустимой рабочей мощностью.

Рис. 6 – Изменение плоскости Рис. 7 – Эллиптический

поляризации волны Н₁₁волновод

Волна Е₀₁

1) Волна является осесимметричной (см. рис. 3), поэтому является чрезвычайно удобной в качестве волны, используемой для передачи электромагнитной энергии в круглом волноводе или для применения в функциональных устройствах на основе круглого волновода (СВЧ фильтры, вращающиеся соединения и т.д.);

2) Волна существует наряду с Н₁₁, следовательно, для предотвращения потерь электромагнитной энергии требуется принятие специальных мер для подавления волны Н₁₁.

Волна Н₀₁

1) У данной волны отсутствуют поперечные составляющие поверхностного тока на стенках волновода (имеются только круговые токи), см. рис. 5. Это приводит к тому, что при увеличении произведения R×¦ коэффициент затухания a данной волны стремится к нулю (см. рис. 5);

2) Наряду с волной Н₀₁ существуют еще по крайней мере четыре типа колебаний (см. табл. 1). В этой связи весьма сложно обеспечить подавления этих паразитных типов колебаний, чтобы добиться тем самым режима с наименьшим коэффициентом затухания электромагнитной энергии в круглом волноводе с волной Н₀₁.

Коаксиальный волновод

В данном вопросе приводится решение уравнений Максвелла применительно к коаксиальной линии передачи.

Коаксиальным волноводом называется направляющая система, образованная двумя изолированными друг от друга соосными, металлическими круглыми проводниками диаметрами 2a и 2b (см. рис. 8).

Рис. 8 – Коаксиальный волновод

Предположим, что волновод заполнен однородной изотропной средой с параметрами e_a, m_a и без потерь (s=0). Пусть сторонние токи отсутствуют, в этом случае 1-ое и 2-ое уравнения Максвелла принимают вид:

Из этих уравнений несложно получить волновые уравнения Гельмгольца:

где: – оператор Лапласа; - постоянная распространения в неограниченной среде с параметрами e_а, m_а.

Выберем в качестве направления распространения волны в коаксиальном волноводе ось z, тогда:

; , (6)

где: b - постоянная распространения в коаксиальном волноводе.

Подставив (6) в уравнение Гельмгольца, получим для напряженности электрического поля следующие выражения:

Или: , (7)

где: - поперечный оператор Лапласа; (k² - b²) = g² – поперечное волновое число.

Характерной особенностью коаксиального волновода является то, что в отличие от прямоугольного и круглого волноводов, в нем могут распространяться три вида направляемых волн:

1) Поперечные (ТЕМ – волны).

2) Электрические (Е – волны).

3) Магнитные (Н – волны).

Для существования ТЕМ – волн в коаксиальном волноводе (т.е. волн, у которых отсутствуют составляющие Е_z и Н_z), как следует из уравнения (7), необходимо выполнение условия:

g² = k² – b² = 0. (8)

Из этого условия следуют два важных вывода:

1) b² = k², или , или l_В = l,

где: l_В – длина волны в коаксиальном волноводе; – длина волны в неограниченной среде с параметрами e_a и m_a.

Таким образом, длина волны в коаксиальном волноводе равна длине волны в неограниченном пространстве.

2) Т.к. , то l_кр = ¥ (f_кр = 0),

где: l_кр, f_кр – критическая длина волны и критическая частота в коаксиальном волноводе.

Это означает, что в коаксиальном волноводе, в отличии от прямоугольного и круглого волновода, сигнал с любой частотой может переносится ТЕМ–волной.

Поэтому, выбором геометрических размеров a и b коаксиального волновода, на практике всегда добиваются того, чтобы мощность сигнала переносилась только ТЕМ – волной. В связи с этим, рассмотрим более подробно распространение ТЕМ – волн в коаксиальном волноводе.

Из уравнения (7) с учетом (8) имеем:

Ñ_^E_m = 0. (9)

Для коаксиального волновода решение данного уравнения проще всего искать в цилиндрической системе координат (r, j, z). Уравнение вида (9) в математике называется уравнением Лапласа, которое имеет следующее решение:

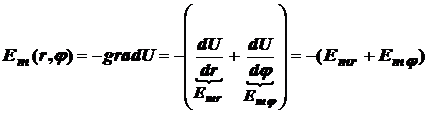где: U – некоторая скалярная функция, подлежащая определению. Определим ее, используя известное из математики тождество: div grad U = 0. Раскрывая операцию div grad в цилиндрической системе координат, получим:

Накладываем граничные условия: касательная составляющая электрического поля Е_j должна быть равна нулю при r = a и r = b. Т.к. , то это означает, что при r = a и r = b. Тогда имеем:

, или .

Отсюда: , соответственно .

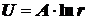При найденном U определяем комплексные значения составляющих электрического поля ТЕМ – волны в коаксиальном волноводе:

Составляющие магнитного поля определяем с помощью второго уравнения Максвелла:

Раскрывая операцию rot в цилиндрической системе координат, получим:

Таким образом, составляющие электромагнитного поля ТЕМ – волны в коаксиальном волноводе имеют вид:

. (10)

На основании уравнений (10) на рис. 9 изображена структура поля ТЕМ–волны в коаксиальном волноводе.

Рис. 9 – Структура поля ТЕМ–волны в коаксиальном волноводе

Дата добавления: 2018-05-12; просмотров: 2970; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!