Исследование тракта модулятор-демодулятор.
4.1) Определим:
· скорость АМ(амплитудной модуляции) 
Скорость модуляции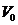 
будет равна скорости выдачи кодовых символов канальным кодером 
· тактовый интервал передачи одного бита 
Тактовый интервал определяется как величина, обратная скорости модуляции
· минимально необходимую полосу пропускания канала 
Минимально необходимая полоса пропускания канала определяется в соответствии с теоремой Найквиста.
· частоту несущего колебания 
· Запишем аналитическое выражение АМ – сигнала в общем виде:
.
Предположим, что 
, тогда
.
Запишем выражения для сигналов, соответствующих передаче 0 и 1
│ 
│ 
Тогда:
.
4.2) Запишем аналитическое выражение, связывающее сигналы на входе и выходе.
Учитывая, что у нас Гауссовский канал с неопределенной фазой, то выражения примут вид:
, где
– сигнал на выходе,
– сигнал на входе,
– шум.
и 
– сигналы, соответствующие приёму 1 и 0.
Тогда:
.
Найдем амплитуду 
. Выразим амплитуду несущего колебания из выражения для вычисления мощности единичного сигнала на передаче:
,
.
Найдем 
. Имеем некогерентный прием, значит:
|
|
|
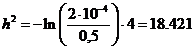
Найдем энергию единичного сигнала из формулы:
, отсюда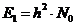 
Найдем мощность единичного элемента сигнала на приеме:
, откуда
, отсюда:
Мы знаем, что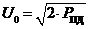 
Ранее получили:
.
Теперь, зная амплитуду несущего колебания 
, и подставив все численные значения, мы можем записать аналитическое выражение, связывающее сигналы на входе и выходе:
4.3) Мы знаем, что если значение начальной фазы приходящего сигнала не известно и может принимать любое значение на интервале 
, то такой метод приема называется некогерентным.
Для вывода правила оптимального некогерентного приема будем исходить из логарифма отношения правдоподобия 
для сигнала 
, 
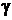– известный коэффициент передачи канала, а 
– случайный сдвиг в канале, тогда: 
.
Здесь 
является случайной величиной, принимающей различные значения при различных . Правило максимума правдоподобия в такой ситуации:
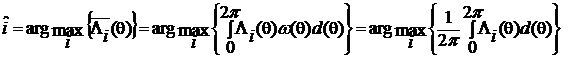
При нахождении 
заметим, что второй интеграл в правой части (предыдущей формулы) от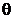 
не зависит и равен энергии 
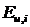сигнала 
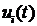на входе канала. Учитывая, что 
, получаем:
|
|
|
,
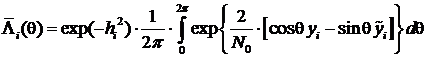где 
, 
.
Обозначив 
и 
, можно записать:
,
где 
– модифицированная функция Бесселя нулевого порядка.
Вместо того, чтобы сравнивать отношения правдоподобия, можно сравнить их логарифмы, что приводит к следующему алгоритму: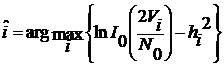 
Для двоичной системы сигналов правило оптимального некогерентного приема выражается неравенством:
При выполнении этого неравенства регистрируется 1, в противном случае регистрируется 0. Итак, изобразим структурную схему, соответствующую данному алгоритму:
Рисунок 7. Схема реализации оптимального приёма дискретных сообщений при неопределённой фазе сигнала
Поясним назначение блоков:
« 
» – перемножители;
«Г1» – генератор опорного сигнала 
;
« 
» – фазовращатель всех сигнальных компонент на π/2 (преобразователь Гильберта);
«∫» – интеграторы;
«БОМ» – блок определения вектора по ортогональным направлениям;
«НУ» – нелинейное безинерционное устройство с характеристикой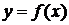 
; «–» – вычитающие устройства.
4.4) Найдем:
· минимально необходимую мощность сигнала на приемной
стороне 
При прохождении сигнала по каналу его амплитуда изменяется в гамма раз. Поскольку мощность сигнала пропорциональна квадрату его амплитуды, то
|
|
|
Ранее мы получили значение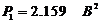 
, и, следовательно
.
· минимально необходимую мощность сигнала на передающей
стороне 
Она так же была получена ранее:
· среднюю мощность сигнала на приеме 
Она рассчитывается по формуле: 
, где 
– мощность сигнала, соответствующего передаче нуля на приеме. Для АМ 
.
4.5) Определимпропускную способность непрерывного канала связи 
.
Учтём, что для расчета 
используется средняя мощность сигнала на приёмной стороне 
.
.
При АМ полоса частот передаваемого сигнала увеличивается в два раза, следовательно, во столько же увеличивается и минимально необходимая полоса пропускания канала:
Вывод: Мы рассчитали пропускную способность непрерывного канала. Она больше скорости модуляции, что говорит о правильно проделанных расчетах.
Пропускная способность непрерывного канала связи больше скорости выдачи информации на выходе кодера. Предельная скорость передачи в канале.
4.6) Ранее мы вычислили, что 
. Теперь определим, как изменится вероятность ошибки на выходе демодулятора при использовании других видов модуляции при сохранении пиковой мощности сигнала:
|
|
|
.
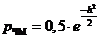
Подставив численные значения, получим:
.
Вывод: Вероятность ошибки при сохранении пиковой мощности для относительной фазовой модуляции меньше по сравнению с частотной и амплитудной модуляцией, следовательно, данный вид модуляции достаточно эффективен.
Задание № 5.
Дата добавления: 2018-05-12; просмотров: 254; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!