Задание 6  Найти частное решение дифференциального уравнения.

1в y'' - 5y' + 6y = (12x - 7)e^-x,        y(0) = y'(0) = 0

2в y'' + y' = e^-x,                               y(0) = 1, y'(0) = 0

3в . y'' - 2y' + 2y = 4e^xcosx,              y(p) = p e^p, y'(p) = e^p

4в y'' + y' = 2cosx ,                         y(0) = 1, y'(0) = 0

5в y'' - y = 4e^x ,                               y(0) = 0, y'(0) = 1

6в y'' - 6y' + 9y = 10sinx,                 y(0) = y'(0) = 0

7в y'' + y = 4xcosx,                          y(0) = 0, y'(0) = 1   

8в y'' - y' = -5e^-x(sinx + cosx),          y(0) = -4, y'(0) = 5

9в y'' + 4y' +5y = 8cosx,                  y(0) = y'(0) = 0  

10в. y'' - 4y' + 5y = 2x²e^x,                   y(0) = 2, y'(0) = 3

 

Задание 7 а) Исследовать на сходимость с помощью признака Даламбера знакоположительный ряд;

б) Исследовать на сходимость с помощью признака Лейбница знакочередующий ряд;

С) Найти радиус сходимости степенного ряда и область сходимости степенного ряда.

1в а)	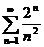1в б)	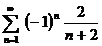1в с)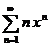
2в а)	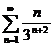2в б)	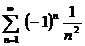2в с)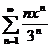
3в а)	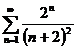3в б)	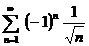3в с)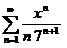
4в а)	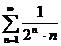4в б)	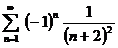4в с)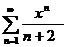
5в а)	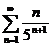5в б)	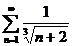5в с)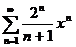
6в а)	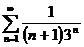6в б)	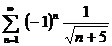6в с)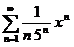
7в а)	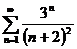7в б)	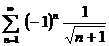7в с)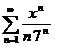
8в а)	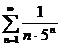8в б)	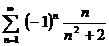8в с)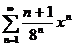
9в а)	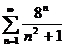9в б)	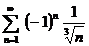9в с)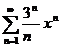
10в а)	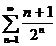10в б)	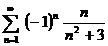10в с)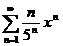

 

Задание 8 Вычислить определенный интеграл с точностью до e = 10^-3 , разложив подынтегральную функцию в степенной ряд и затем почленно проинтегрировав.

 

 

 

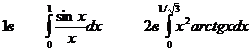
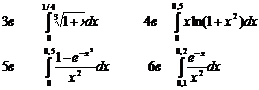
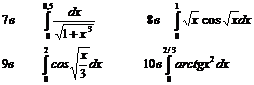
Нулевой вариант

Пример1     Вычислить неопределенный интеграл: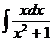  

Т.к. 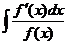, то f(x) = t

 =  =

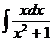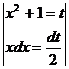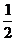
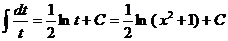
Пример 2    Вычислить неопределенный интеграл:

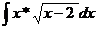
Решение: Воспользуемся методом подстановки:

 

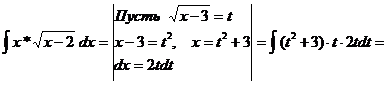
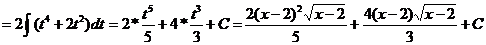
Пример 3   Вычислить неопределенный интеграл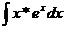  

 

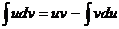
Пусть x = u(x)	ex dx = dv
Тогда х'dx = u(x) ' dх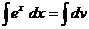
dx = du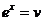

 

В результате получим: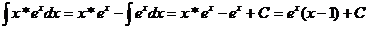

Пример 4 Вычислить неопределенный интеграл:

 

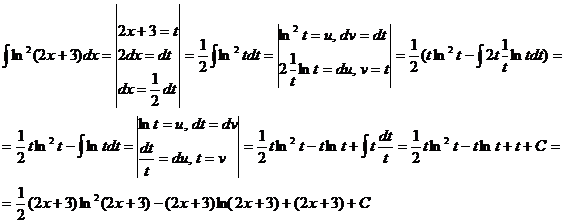
Некоторые виды интегралов, интегрируемых по частям:

1 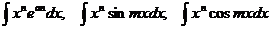  - xⁿ = u, dv = остальное;

2 - x^kdx = dv, u- остальное

 

Пример 5    Вычислить неопределенный интеграл:

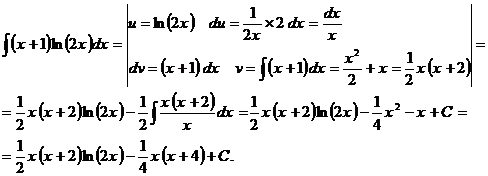
Пример 6    Вычислить неопределенный интеграл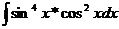

 

 =

 

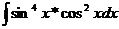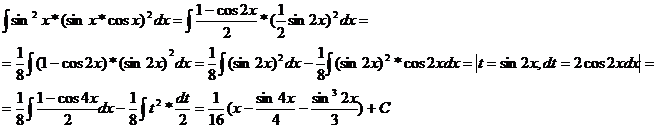
Пример 7  Вычислить определенный интеграл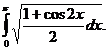  

 

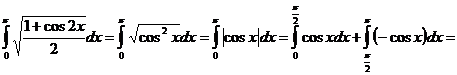
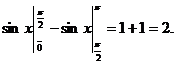
Пример 8 Вычислить несобственный интеграл (или установить его расходимость) .

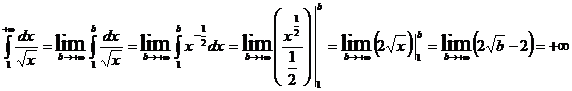
Данный несобственный интеграл расходится

Пример 9      Вычислить несобственный интеграл или установить его расходимость.

 

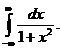
Подынтегральная функция четная, поэтому:

 

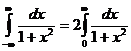
Найдем

.

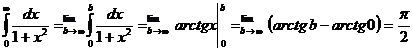Тогда

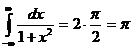т.е. несобственный интеграл сходится.

Ответ: .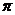

 

 

Дифференциальным уравнением 

Пример 1 Решить уравнение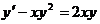

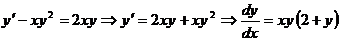. Умножим обе части на 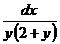, получим 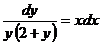. Проинтегрируем полученное уравнение 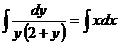. Представим 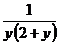, как 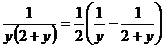, тогда

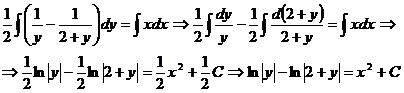
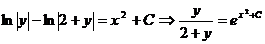
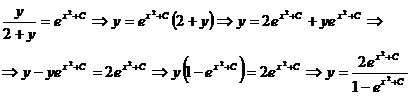
Пример 2 Решить уравнение: .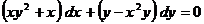

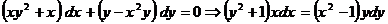. Разделив обе части на 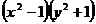, получим 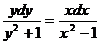. Проинтегрируем полученное уравнение:

.

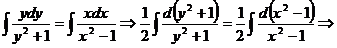
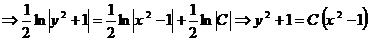Пример 3 Найти общее решение (общий интеграл) дифференциального уравнения первого порядка у'=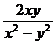

Решение. Правая часть уравнения задает свойством f(λх,λу)= f(x,y).

 Поэ­тому заданное уравнение является однородным дифференциальным уравнением первого порядка. Совершим замену и=у/х, где и — некоторая функция от аргумента х. Отсюда у=их,

 у'=и'х+и. Исходное уравнение приобретает вид и'х+и=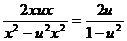

 

Продолжаем преобразования: и'х = 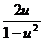 -и=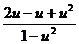

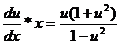
Производим разделение переменных:

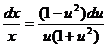
После интегрирования обеих частей уравнения получаем 

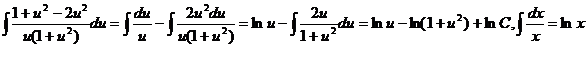
Таким образом lnu-ln(1+u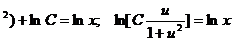

Потенцируя, находим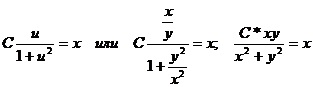

Итак, общий интеграл исходного уравнения приобретает вид: Су=х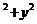

 

 

 Пример 4 Найти частное решение дифференциального уравнения у'+ 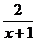 у= (х+1)  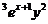удовлетворяющее начальному условию у(0) =1.

 

Решение. Заданное дифференциальное уравнение является уравнением Бернулли. Полагаем у= иv, где и, v —неиз­вестные функции от х. Тогда

 у' = и'v + иv '. Подставляя у и у' в ис­ходное уравнение, будем иметь

и'v + иv '+ 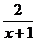 иv =(х+1)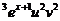

и'v + и [v '+ 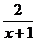v]= (х+1)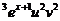

Подберем функцию v=v(х) так, чтобы выражение, содер­жащееся в квадратной скобке, обращалось в нуль. Для опре­деления v(x) имеем дифференциальное уравнение с разделяющимися переменными.

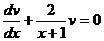Откуда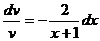

 После интегрирования получим

lnv= — 2ln(х+1), т. е.

v=1/(x+1)²

 Для определения функции и(х) имеем

 и'v=(х+1)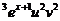

или и'=(х+1) )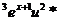

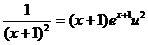
Это дифференциальное уравнение с разделяющимися переменными относительно неизвестной функции и(х). Разделим переменные, будем иметь

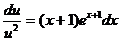
Интегрируя обе части равенства, получаем 

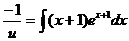
Последний интеграл вычисляем методом интегрированя по частям, в результате чего имеем

и=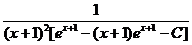

Используя начальное условие, вычислим соответствующее ему значение постоянной С .

У(0)= -1/С=1 т.е. С=-1 .

Поэтому частное решение исходного дифференциального уравнения, удовлетворяющее заданному начальному условию.имеет вид

У=(х+1)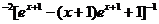

 

Пример 5

y ^¢¢ – 4y ¢ + 13y = 40 ∙ cos 3x.

Решение: Общее решение ЛНДУ имеет вид y = y + y*. Находим решение однородного уравнения y :

y^¢¢ – 4y^¢ + 13y = 0. Характеристическое уравнение

k² – 4k + 13 = 0 имеет корни k₁ = 2+3i, k₂ = 2-3i. Следовательно,

 y = e^2x ∙ (c₁ ∙ cos 3x + c₂ ∙ sin 3x).

Находим частное решение y*. Правая часть ЛНДУ в нашем случае имеет вид

 f(x) = e^{0 x} ∙( 40 cos 3x + 0 ∙ sin 3x). Так как α = 0, β = 3, α + βi = 3i не совпадает с корнем характеристического уравнения, то r =0 . Согласно формуле, частное решение ищем в виде y* = А cos3x + B sin3x. Подставляем y* в исходное уравнение. Имеем:

 (y*)^¢ = -3A sin3x + 3B cos3x,

 (y*)^¢¢ = -9Acos3x – 9Bsin3x

Получаем: -9Acos3x – 9Bsin3x – 4(-3A sin3x + 3B cos3x)+13(Acos3x +Bsin3x)= 40 cos3x

или (-9A-12B+13A)cos3x+(-9B+12A+13B)sin3x = 40cos3x + 0∙ sin3x

отсюда имеем:

                      4А – 12В = 40,

                      12А + 4В = 0

Следовательно, А = 1, В = -3. поэтому y*= cos3x – 3sin3x. И наконец,

 y = e^2x(c₁∙cos3x + c₂ ∙ sin3x) +cos3x – 3sin 3x – общее решение уравнения.

 

Пример 6 Указать вид частного решения дифференциального уравнения .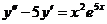

Решение. Это линейное уравнение неоднородное дифференциальное уравнение 2 порядка с постоянным коэффициентами. Согласно теории таких уравнений (см. Приложение 2, В) сначала решаем характеристическое уравнение

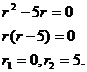
Затем правую часть уравнения представляем в виде

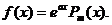
Получим 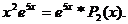 Здесь,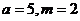

Частное решение, определяемое по правой части, будем иметь вид

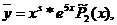
Где S - показатель кратности числа 5 как корня характеристического уравнения(S=1)

Итак, 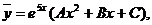 или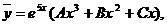

 

Пример 7 Найти общее решение уравнения: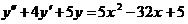

 

Решение:

Найдем корни характеристического уравнения: 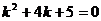, тогда 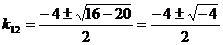, следовательно 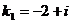, , тогда

фундаментальную систему решений образуют функции:

,

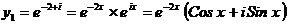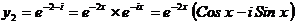
Т.к. действительные и мнимые решения в отдельности являются решениями уравнения, то в качестве линейно независимых частей решени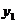й  и 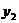, возьмем 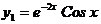, , 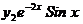тогда общее решение однородного уравнения будет иметь вид: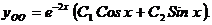

Представим правую часть уравнения, как 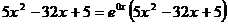 и сравним с выражением, задающим правую часть специального вида:

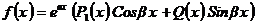. Имеем 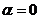, , 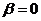тогда т.к.  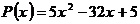- многочлен второй степени, то общий вид правой части: 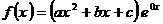. Найдем частные решения:

, ,

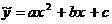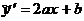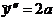
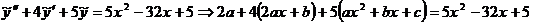
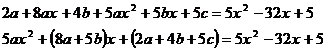
Сравним коэффициенты при 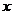 слева и справа, найдем 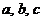, решив систему:

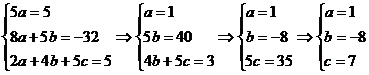, отсюда .

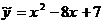Тогда общее решение заданного неоднородного линейного уравнения имеет вид: .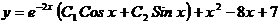

 

Пример 8    Найти решение дифференциальных уравнений: (х² – у²) у¢ - 2 ух = 0

Решение      Полагая у = ux, находим у¢= u¢x + u, получаем

(x² – (xu)²) (u¢x + u) – 2ux × x = 0, u¢ = 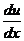. Сокращаем на х² 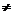0, получаем уравнение с разделяющимися переменными:

(1 – u²) (x du +u dx) – 2u dx = 0   

(1 – u²) x du + (1 – u²) u dx – 2u dx = 0

(1 – u²) x du = - (- u – u³) dx , умножаем обе части уравнения на 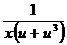, получаем

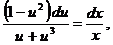 интегрируя, получаем 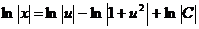, откуда ,

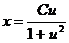подставляя 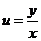, получаем общее решение дифференциального уравнения х² + у² = Су.

 

Пример 9 Найти общее и частное решение дифференциальных уравнений, удовлетворяющее начальным условиям: у¢+ у = х + 2, у = 0 при х = -1

Решение  Пусть у = uv, тогда y¢= u¢v + uv¢.

Подставляя выражения у и у¢ в уравнение, получим

u¢v + uv¢ + uv = x + 2,

u (v¢ + v) = x + 2 - u¢v.

Полагаем, что v¢ + v = 0, тогда 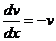, интегрируем, получаем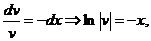

.

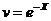Если v¢ + v = 0, то уравнение u (v¢ + v) = x + 2 - u¢v примет вид x + 2 - u¢v = 0, где v = e^-x, то

x +2 - u¢ e^-x = 0 , u¢ = (x + 2) e^x, u¢ = 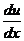, тогда du = (x + 2) e^x dx, интегрируя, получим

u = ,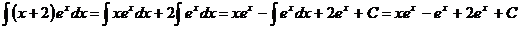

u = xe^x + e^x + C

Следовательно, у = uv, то решение у = е^-х [C + e^x (x + 1)] = Ce^-x + x + 1

Найдем частное решение при начальных условиях у = 0, х = -1.

В общее решение подставляем начальные условия, получаем:

Се¹ + (-1) + 1 = 0, С = 0, тогда частное решение у = х +1

 

Пример 9   Решить уравнение y^´´ – 6y^´ + 10y = 24 ∙ cos 2x.

Решение: Общее решение ЛНДУ имеет вид y = y + y*.

 y^´´ – 6y^´ + 10y = 0.

k² – 6k + 10= 0

k₁ = 3+i, k₂ = 3-i.

y = e^3x ∙ (c₁ ∙ cos x + c₂ ∙ sin x).

Находим частное решение y*.

f(x) = e⁰*^x ( 24 cos 2x + 0 ∙ sin 2x).

 y* = А cos2x + B sin2x.

(y*)^´ = -2A sin2x + 2B cos2x,

 (y*)^´´ = -4Acos2x – 4Bsin2x

Получаем: - 4Acos2x – 4Bsin2x – 6(-2A sin2x + 2B cos2x)+10(Acos2x+ Bsin2x)= 24 cos2x

или (-9A-12B+13A)cos3x+(-9B+12A+13B)sin3x = 40cos3x + 0∙ sin3x

отсюда имеем:

                      А=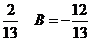

y*= 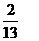cos2x + 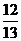sin2x. И, наконец,

 y = e^3x(c₁∙cosx + c₂ ∙ sinx) + 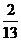cos2x + 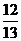sin 2x – общее решение уравнения.

Пример 10

Исследовать сходимость ряда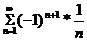               

Решение: Это знакочередующийся ряд, для которого выполнены условия признака Лейбница:

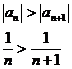
Члены ряда, взятые по абсолютной величине, составляют убывающую последовательность.

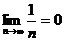, т.е. общий член ряда стремится к нулю при .

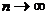Следовательно, оба условия признака Лейбница выполняются и указанный ряд сходится. Однако ряд, составленный из членов данного ряда, взятые по абсолютной величине, т.е. ряд

1+ 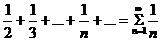 - расходится (гармонический ряд) 

Тогда исследуемый ряд сходится условно.                          

Пример 11

Найти область сходимости ряда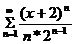                                             

Решение: Находим радиус сходимости ряда по формуле:

 

R =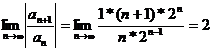  

Следовательно, ряд сходится при -2 < x + 2 < 2, т.е. при – 4 < x < 0, т.е. при х 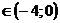- интервал сходимости ряда.

При x = - 4 имеем ряд

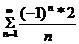 - знакочередующийся ряд, который сходится по признаку Лейбница.

При x = 0 имеем расходящийся ряд

                               =

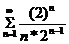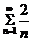
Следовательно, областью сходимости исходного ряда [-4; 0), т.е. при х 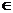 [-4; 0) ряд сходится, при остальных значениях х ряд расходится.

---

Дата добавления: 2018-05-12; просмотров: 735; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!