Устойчивость состояний равновесия: критерий Сильвестра
По Ляпунову: Устойчивое состояние равновесия системы такое, когда при малом начальном отклонении системы все ее точки будут двигаться не уходя от положения равновесия далее наперед заданного расстояния.
Критерий Сильвестра:
Система находится в положении устойчивого равновесия, если квадратичная формула потенциальной энергии этой системы положительна, что возможно в том случае, если все главные диагональные миноры матрицы квадратичной формы и положительны.
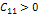
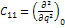
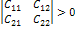
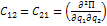
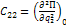
Общее уравнение динамики
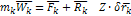
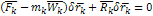
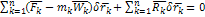
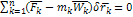 (1) – общее уравнение динамики
(1) – общее уравнение динамики
Уравнение (1) запишем в виде:
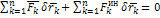
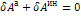 - общее уравнение динамики – принцип Доломбера - Лагранжа:
- общее уравнение динамики – принцип Доломбера - Лагранжа:
При движении механической системы с идеальными связями работа всех активных сил и сил инерции на любом возможном перемещении системы равна нулю.
Кинетическая энергия в обобщенных координатах
Для нестационарных связей радиус – вектор 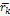 зависит от всех обобщенных координат и времени t.
зависит от всех обобщенных координат и времени t.
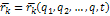 ;
; 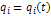 ;
; 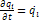
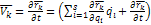 (1)
(1)
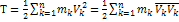 i=1,2,…,s
i=1,2,…,s
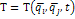
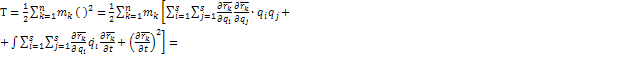
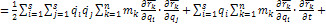
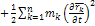 В пустых скобках выражение (1)
В пустых скобках выражение (1)
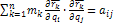
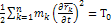
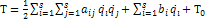
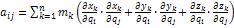
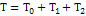
В общем случае кинетическую энергию материальной системы можно представить суммой квадратичной 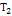 , линейной
, линейной 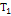 и нулевой
и нулевой 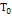 форм относительно обобщенных скоростей.
форм относительно обобщенных скоростей.
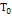 - нулевая ступень обобщенных скоростей
- нулевая ступень обобщенных скоростей
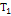 - линейная функция обобщенных скоростей
- линейная функция обобщенных скоростей
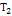 - квадратичная степень обобщенных скоростей
- квадратичная степень обобщенных скоростей
Для стационарных связей: 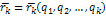
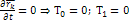
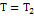
Одна степень свободы:
|
|
|
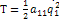
Две степени свободы:
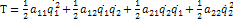
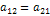
Уравнение Лагранжа II рода
Из формулы 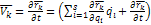 :
:
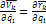
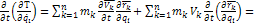
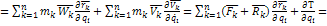
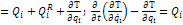
Связи идеальные:
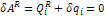
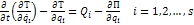
Силы только потенциальны:
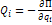
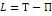 (кинетический потенциал, функция Лагранжа)
(кинетический потенциал, функция Лагранжа) 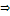
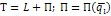
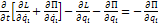
Обыкновенное однородное ДУ 2-го порядка (с нулевой правой частью):
 “2S”
“2S”
Число уравнения равно числу степеней свободы.
Виртуальная работа
Виртуальная работа – работа сил на виртуальных перемещениях системы
Пусть система материальных точек занимает в некоторый момент
времени t какое-то положение. Обозначим через Fk силы, приложенные к точкам системы. Из данного положения при фиксированном времени t, сообщим системе виртуальное перемещение δrk. Будем считать, что на этом перемещении силы Fk, приложенные к системе, не изменяются.
Составим сумму работ этих сил на вирт. перемещении δrk
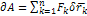
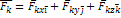
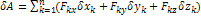
14. Интеграл движения: обобщенный интеграл движения
f 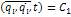 (где С - константа)
(где С - константа)
Интеграл системы уравнений 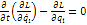 (1), или интегралом движения, или первым интегралом, если при подстановке вместо
(1), или интегралом движения, или первым интегралом, если при подстановке вместо 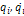 решений системы (1), функция f обращается в константу.
решений системы (1), функция f обращается в константу.
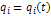
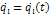
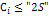
Системы уравнений (1) может иметь не более “2S” – первых интегралов.
Первые интегралы уравнений Лагранжа II-го рода бывают 2-х видов:
|
|
|
1)Обобщенные интегралы энергии.
2)Циклический интеграл.
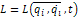
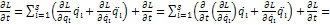
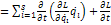
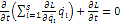
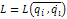 L от времени не зависит
L от времени не зависит
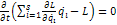
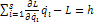 (2) - обобщенный интеграл энергии или интеграл Якоби
(2) - обобщенный интеграл энергии или интеграл Якоби
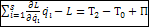
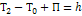
Допущение: 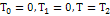
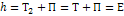 - обычный интеграл
- обычный интеграл
Консервативная система – система, которая обладает обычным интегралом энергии.
Из (2) сумма отбрасывается: первый интеграл получается из (2):
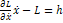
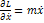
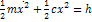
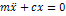
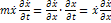
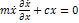
Дата добавления: 2018-05-12; просмотров: 619; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
