Тема 2.Статистическое изучение вариации

Тема 1.Средние величины

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.

Виды средних величин: 1) арифметическая;

2) гармоническая;

3) геометрическая;

1) Средняя арифметическая.

а) Средняя арифметическая простая применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц (наиболее распространенная).

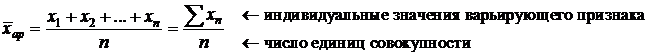
б) Средняя арифметическая взвешенная – средняя сгруппированных величин, вычисляется по формуле:

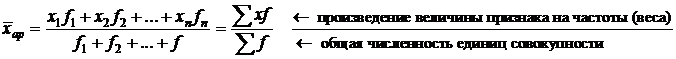Пример 1.

Таблица 1

АО с размером дивидендов, руб/	Число АО, ( )	Середина интервала ( )
7 – 130 130 – 253 253 – 376 376 – 499 499 – 622 622 – 745 745 – 868 868 – 991	13 12 7 13 16 12 13 14	68,5 191,5 314,5 437,5 560,5 683,5 806,5 929,5	890,5 2298,0 2201,5 5687,5 8968,0 8202,0 10484,5 13013,0
ИТОГО	100	-	51745,0

В данном случае следует воспользоваться формулой средней арифметической взвешенной. Поскольку интервальные значения признака встречаются не один раз, и эти числа повторений (частоты) не одинаковы.

Конкретными значениями признака, которые должны непосредственно участвовать в расчетах, служат середины интервалов (но не средние в интервалах значения), а весами частоты.

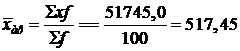руб.

Данный результат отличается от полученного, на основе средней арифметической простой. Это объясняется тем, что в расчете на основе ряда распределения мы располагаем не индивидуальными исходными данными, а лишь сведениями о величине середины интервала.

Часто приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним), т.е. среднюю из средних. Так, например, средняя продолжительность жизни граждан страны представляет собой среднее из средних продолжительностей жизни по отдельным регионам данной страны.

Среднее из средних величин вычисляется по следующей формуле, считая :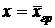

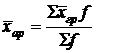где 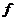– число единиц в каждой группе.

2) Средняя гармоническая.

Применяется в тех случаях, когда не известны частоты 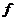по отдельным вариантам x совокупности, а представлено их произведение 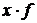. Обозначим это произведение через 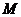, тогда получим формулу средней гармонической взвешенной:

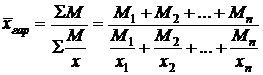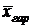является преобразованной формой 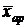и тождественна ей. Вместо 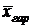всегда можно рассчитать 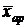, но для этого нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

Пример 2.

Таблица 2

АО с размером дивидендов, руб	Середина интервала ( 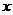)	Общий размер дивидендов в группе, руб.( )
7 – 130 130 – 253 253 – 376 376 – 499 499 – 622 622 – 745 745 – 868 868 – 991	68,5 191,5 314,5 437,5 560,5 683,5 806,5 929,5	890,5 2298,0 2201,5 5687,5 8968,0 8202,0 10484,5 13013,0
ИТОГО	-	51745,0

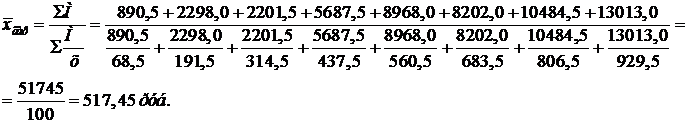
3) Средняя геометрическая.

Применяется, когда индивидуальные значения признака характеризует средний коэффициент роста (представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики). Вычисляется по формуле:

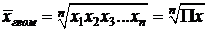
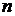– число вариантов; 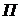– знак произведения.

Наиболее широко применяется для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Структурные средние

Помимо степенных средних в статистической практике используются структурные средние, в качестве которых рассматриваются мода и медиана. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака.

Мода ( 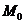)– значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту.

Широко используется при изучении покупательского спроса, регистрации цен и т.п.

Формула для вычисления:

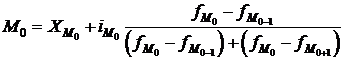где 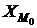– нижняя граница модального интервала;

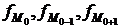– частоты в модальном, предыдущем и следующем за модальным интервалом (соответственно).

Модальный интервал определяется по наибольшей частоте.

Пример: По таблице 1 рассчитаем моду. Наибольшая частота 16 в интервале [499 – 622), следовательно это и есть модальный интервал.

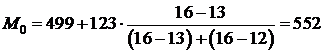руб.

Итак, чаще всего встречаются АО с размером дивидендов 552 рубля.

Медиана 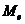– варианта, которая находится в середине вариационного ряда.

Делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значением признака больше медианы.

Номер медианы для нечетного числа членов ряда вычисляется по формуле:

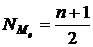
где 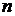– число членов ряда.

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

Вычисляется медиана по формуле:

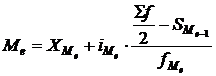
где 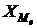– нижняя граница медианного интервала;

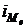– медианный интервал;

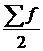– половина от общего числа наблюдений;

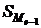– сумма наблюдений, накопленная до начала медианного интервала;

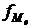– число наблюдений в медианном интервале.

Пример 3: По таблице 1 найдем медиану (медианный интервал [499 – 622), так как половина накопленных частот принадлежит этому интервалу):

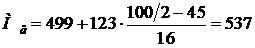руб.

Следовательно, половина АО имеет дивиденды больше 537 руб., а половина меньше этого значения.

Соотношения между средней арифметической, медианой и модой в статистических распределениях. Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить асимметрию ряда распределения.

Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.

Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части – квартили, на пять – квинтили, на десять – децили, на сто – перцентили.

Тема 2.Статистическое изучение вариации

Понятие вариации. При изучении совокупности явления нельзя ограничиваться только нахождением средней величины. Средние величины дают обобщенную характеристику варьирующего признака, показывают типичные характеристики для изучаемой совокупности. Однако в средней величине не проявляется степень колеблемости отдельных значений признаков вокруг среднего уровня. В зависимости от однородности в совокупности колеблемость признаков может быть большой или малой. Поэтому возникает необходимость в измерении вариации отдельных вариантов по отношению к средней величине.

Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Вариация в переводе с латинского означает «колеблемость», «изменчивость», «непостоянство». Предполагая, что большинство социально-экономических явлений и процессов варьируют в некотором масштабе, статистика разработала методологию расчета показателей вариации, которые, в свою очередь, могут быть абсолютными, относительными и средними.

Показатели вариации. К показателям вариации относятся: размах вариации, среднее линейное (абсолютное) отклонение (с.л.о.), дисперсия, среднее квадратическое отклонение (с.к.о.), коэффициент вариации.

1) Размах вариации – разность между максимальным и минимальным значением признака:

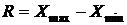Он характеризует пределы изменения признака.

Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.

Простейший показатель такого типа среднее линейное отклонение.

2) Среднее линейное отклонение – представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (учитывает только крайние значения признака и не учитывает все промежуточные).

– среднее линейное отклонение для несгруппированных данных:
,

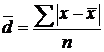где 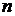– число членов ряда.

То есть среднее линейное отклонение равно средней арифметической из абсолютных отклонений (модулей) признака всех единиц совокупности от средней арифметической.

–для сгруппированных данных: ,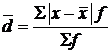

где 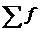– сумма частот вариационного ряда.

В формулах разности в числителе взяты по модулю, иначе в числителе всегда будет ноль – алгебраическая сумма отклонений вариантов от их средней арифметической.

Поэтому среднее линейное отклонение применяют редко, только в случаях, когда суммирование показателей без учета знаков имеет экономический смысл. Например, анализ состава рабочих, ритмичность производства, оборот внешней торговли и др.

3) Дисперсия – это средний квадрат отклонений индивидуальных значений от средней арифметической (не имеет единиц измерения).

В общем виде взвешенная дисперсия исчисляется по формуле:

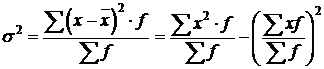
или простая дисперсия:

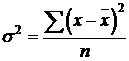4) Среднее квадратическое отклонение ‑ это есть квадратный корень из среднего квадрата отклонений отдельных значений признака от средней арифметической:

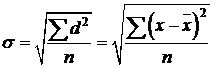– для несгруппированных данных;

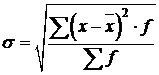– для сгруппированных данных (для вариационного ряда).

Коэффициент вариации. В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией зарплаты, выраженной в рублях.

Для осуществления такого сравнения, а также сравнения колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации – коэффициент вариации.

Коэффициент вариации – представляет собой выраженное в процентах отношение СКО к средней арифметической.

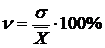это и есть коэффициент вариации. Это относительная мера вариации и позволяет сравнивать степень варьирования в разных вариационных рядах.

Рассмотрим расчет показателей вариации.

Пример. По исходным данным (таблица 1) определить: размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Решение:

1) 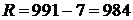руб.

Таблица

АО с размером дивидендов, руб.	Число АО ( )	Середина интервала ( )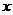
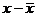
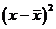
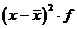
7 – 130 130 – 253 253 – 376 376 – 499 499 – 622 622 – 745 745 – 868 868 – 991	13 12 7 13 16 12 13 14	68,5 191,5 314,5 437,5 560,5 683,5 806,5 929,5	890,5 2298 2201,5 5687,5 8968 8202 10484,5 13013	-448,95 -325,95 -202,95 -79,95 43,05 166,05 289,05 412,05	201556,1 106243,4 41188,7 6392,003 1853,303 27572,6 83549,9 169785,2	2620229,33 1274920,83 288320,92 83096,03 29652,84 330871,23 1086148,73 2376992,84
ИТОГО	100	–	51745	–	–	8090232,75

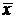– среднее значение находили в примере 1, оно равно 517,45 руб.

2) дисперсия: .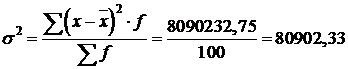

3) среднее квадратическое отклонение: 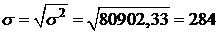руб.

4) коэффициент вариации: .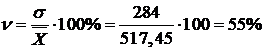

Анализ полученных данных говорит о том, что размер дивидендов АО отличается от среднего размера ( 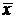=517,45) в среднем на 284 рубля, или на 55 %. Значение коэффициента вариации превышает 33 %, следовательно, вариация размера дивиденда велика, найденный средний размер дивиденда плохо представляет всю совокупность АО, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по размеру дивидендов.

Виды дисперсии.

Дисперсия – это средний квадрат отклонений всех значений признака ряда распределения от средней арифметической.

Если совокупность данных сгруппирована на группы по какому-то признаку, то в этом случае выделяются 3 вида дисперсий:

- Общая дисперсия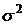

– Средняя из внутригрупповых дисперсий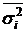

- Межгрупповая дисперсия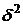

Общая 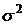- измеряет вариацию во всей совокупности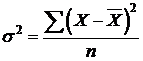

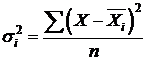– внутригрупповая 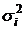- измеряет вариацию признака внутри группы, 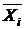- групповая средняя.

Средняя из внутригрупповых дисперсий исчисляется ,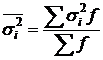

где 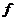– частота появления внутригрупповой дисперсии одной величины (одного размера).

Межгрупповая дисперсия 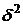– измеряет колеблемость групповых средних 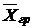вокруг общей средней :

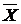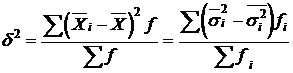
Она измеряет вариацию, обусловленную признаком, положенным в основу группировки.

Правило сложения дисперсий.

Общий закон (правило) сложения дисперсий ‑ Общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии.

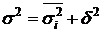
Показывает значение фактора, положенного в основу группировки (из всей совокупности факторов).

Коэффициент детерминации – есть квадрат эмпирического корреляционного отношения.

Эмпирическое корреляционное отношение – есть корень квадратный из отношения межгрупповой дисперсии к общей:

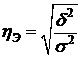– характеризует влияние группировочного признака на результативный признак (оба показателя (числитель и знаменатель) не превышают по своей величине единицы: чем больше показатели в этих пределах, тем теснее взаимосвязь между изучаемыми признаками).

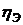; – влияние других факторов равно 0.

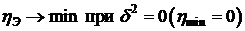– влияние признака равно 0.

Дата добавления: 2018-05-12; просмотров: 377; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!