Классификация по максимуму правдоподобия.

 

Классификация по максимуму правдоподобия – наиболее универсальный из «классических» методов классификации с обучением, поскольку позволяет не только разделять классы с различными типами функций плотности распределения признаков, но и минимизировать в среднем ошибки классификации. Поэтому мы остановимся на данном методе более подробно.

Метод основывается на так называемом критерии Байеса из теории проверки статистических гипотез [16]. Под гипотезой в нашей задаче понимается принадлежность пикселя изображения какому-то определенному классу. Для простоты рассмотрим теоретические основы принятия решения по критерию Байеса на примере одномерного признака X и двух классов. Задача заключается в определении на шкале Х интервалов W₁ и W₂, на которых будут приниматься решения в пользу первого и второго класса соответственно. В дальнейшем классы и соответствующие им области принятия решения будем обозначать одним и тем же символом W. 

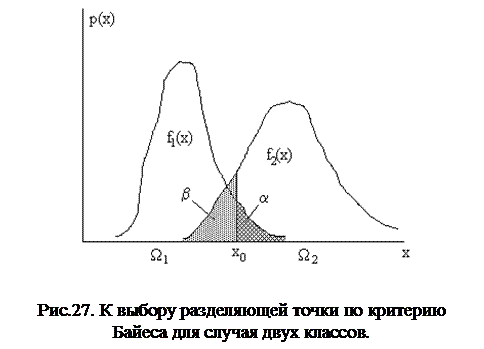
Предположим, что на основе обучающих выборок мы построили функции плотности статистического распределения f₁(x) и f₂(x) (рис.27). Заметим, что в  общей постановке задачи f₁(x) и f₂(x) не обязательно соответствуют нормальному распределению.

В общем случае мы должны также учесть априорные вероятности Р(W₁) и Р(W₂) появления данных классов. Для задачи классификации пикселей изображения земной поверхности априорные вероятности - это ожидаемые доли площади под каждым классом, которые могут быть получены, например, из фондовых материалов. То есть появление в некотором классе W_k пикселя со значением x_i (в случае нескольких каналов, соответственно, определенного вектора x) на изображении конкретной территории соответствует одновременному осуществлению двух независимых событий:

1) пиксель принадлежит объекту класса W_k;

2) пиксель принял значение x_i. 

Вероятность одновременного осуществления двух независимых событий есть произведение вероятностей каждого из этих событий:

 

P({W=W_k}Ç({x= x_i})= P(W=W_k)× P(x= x_i)=P(W_k) f_k(x_i). (24)

 

    Итак, вероятности появления некоторой произвольной точки x для первого и второго классов будут равны, соответственно, P(W₁) f₁(x) и P(W₂) f₂(x). Заметим, что эти вероятности не равны нулю на всем интервале значений признака X, как для первого, так и для второго классов. То есть при любом значении x, принимая решение в пользу какого-то одного класса, мы рискуем совершить ошибку. И мы должны выбрать границу между классами на шкале X таким образом, чтобы как-то минимизировать эти ошибки.

В критерии Байеса для получения такого условия вводится понятие «среднего риска» - средней платы за ошибки при многократном принятии решения, и это как раз подходит для решения нашей задачи. При классификации изображения мы отдельно классифицируем каждый пиксель, и хотим, чтобы по всему изображению в среднем ошибки классификации были как можно меньше.

Рассмотрим все возможные ситуации при принятии решения в случае двух классов. Назовем событие «при данном значении x имеет место класс W₁ с функцией плотности распределения f₁(x)»  гипотезой H₁, а событие «при данном значении x имеет место класс W₂ с функцией плотности распределения f₂(x)»  - гипотезой H₂.

Пусть мы выбрали точку x₀, разделяющую два класса (рис.27). Вероятность появления любого значения х отлична от нуля и для первого, и для второго класса на всем множестве Х, поэтому при попадании значения x в одну из двух определенных нами областей могут возникнуть 4 ситуации.

1. Принимаем гипотезу Н₁, и она верна.

2. Принимаем Н₂, но верна Н₁ .

3. Принимаем Н₂, и она верна.

4. Принимаем Н₁, но верна Н₂.

При равных априорных вероятностях появления классов P(W₁)=P(W₂) полная вероятность возникновения ситуации 1 соответствует площади под f₁(x) на полуинтервале (-¥,х₀], ситуации 2 - площади под f₁(x) на интервале (х₀,¥), ситуации 3 - площади под f₂(x) на (х₀,¥), ситуации 4 - площади под f₂(x) на   (-¥,х₀].

Суммарная площадь под f₁(x) и f₂(x) для ситуаций 2 и 4 - это полная вероятность ошибок в нашей схеме принятия решений. В случае двух альтернативных гипотез ошибку, соответствующую ситуации 2, обычно называют ошибкой первого рода(a), ошибку, соответствующую ситуации 4, - ошибкой второго рода(b). Вообще говоря, понятие ошибок первого и второго рода симметрично и зависит от того, какая гипотеза является основной, а какая – альтернативной. Если бы H₂ была основной гипотезой, ошибка первого рода соответствовала бы ситуации 4.

При классификации пикселей многозональных аэрокосмических изображений ошибка первого рода проявляется в появлении на объектах класса W₁ точек посторонних классов. В свою очередь, ошибки второго рода проявляются в появлении точек этого класса на других объектах. Когда количество выделяемых классов невелико, обычно преобладают ошибки второго рода, поскольку аналитик не учитывает все присутствующие на изображении типы объектов, в том числе и с характеристиками, близкими к выделяемым классам. Это одна из причин, по которой полезно выполнение предварительной неконтролируемой классификации, причем на значительно большее, чем требуется, количество классов. Неконтролируемая классификация позволяет предварительно оценить величину ошибок второго рода, более точно определить границы искомых классов и, при необходимости, разумно задать область отказов от распознавания, соответствующую классу «прочее».  

Для расчета «среднего риска» введем плату за каждую из четырех ситуаций – платежный коэффициент c_ij, где индекс i соответствует ситуации «имеет место гипотеза i», а индекс j соответствует ситуации «мы приняли гипотезу j».

Рассматривая платежные коэффициенты c_ij как “риск” в каждой из возможных ситуаций (которые можно рассматривать как случайные события), введем понятие среднего риска для наших четырех случаев:

 

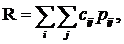 i,j=1,2. (25)

    Здесь c_ij - это выплаты в каждой ситуации (платежные коэффициенты), а p_ij – вероятности соответствующих выплат. В случае, когда с₁₁=с₂₂=0 и с₁₂=с₂₁=1 (здесь «плата» - это штраф за ошибки), функцию R называют также функцией потерь.

Как было сказано выше, чтобы получить вероятности p_ij, мы должны посчитать площади под соответствующими каждому случаю частями f₁(x) и f₂(x), то есть взять интеграл от этих функций на соответствующем интервале. Если априорные вероятности появления классов не одинаковы, то мы должны их учесть в соответствии с выражением (24).

Следовательно, в общем случае формулу (25) можно записать так:

R=с₁₁ Р(W₁) 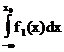+с₁₂ Р(W₁) 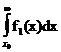+с₂₂ Р(W₂) 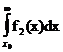+с₂₁ Р(W₂) 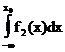. (26)

Выражение (26) есть полный средний риск так называемой стратегии Байеса. Минимум R в точке х₀ достигается при условии

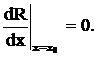
Возьмем производную в точке х₀, учитывая, что ,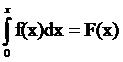

F(-¥)=0, F(¥)=1:

 

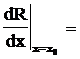 с₁₁ Р(W₁) f₁(x)- с₁₂ Р(W₁) f₁(x)- с₂₂ Р(W₂) f₂(x) + с₂₁ Р(W₂) f₂(x) =0. (27)

 

Отсюда имеем следующее соотношение для х=х₀:

 

. (28)

 

Отношение (28) называется отношением правдоподобия, а величина l - коэффициентом правдоподобия. При значениях 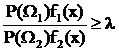 решение принимается в пользу W₁, при  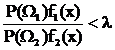- в пользу W₂. 

Функции, стоящие в числителе и знаменателе, определенные ранее выражением (24), называются функциями правдоподобия для классов W₁ и W₂ соответственно.

Если положить, что с₁₁=с₂₂=0 и с₁₂=с₂₁=1, получим:

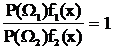 или, в логарифмической форме, 

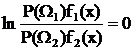. (29)

 

Когда значения признака для обоих классов распределены по нормальному закону (см. выражение (1) в разделе 5) со средними m₁, m₂ и среднеквадратическими отклонениями s₁, s₂ соответственно, отношение правдоподобия в логарифмической форме имеет вид:

 

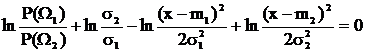
. (30)

 

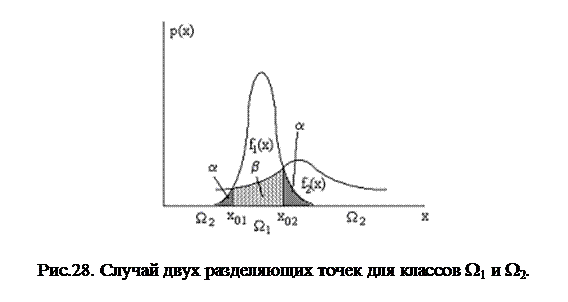
То есть х₀ является решением квадратного уравнения. Случай, когда уравнение имеет два действительных корня, представлен на рис.28.

Все полученные выше результаты справедливы и когда образ представлен не значением одного параметра, а n-мерным вектором х.

Логарифм отношения правдоподобия (29) в данном случае соответствует понятию разделяющей функции, которое мы ввели в разделе 7.2. Разделяющая функция d_ks(x)=0 для классов k и s при нормально распределенных значениях признака x в многомерном случае выглядит так:

 

ln 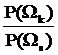+(1/2)ln 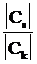-(1/2)(x-m_k)^TC_k^-1(x-m_k)+(1/2)(x-m_s)^TC_s^-1(x-m_s)=0. (31)

 

В общем случае такие разделяющие функции в n-мерном пространстве Х представляют собой гиперповерхности сложной формы - так называемые гиперквадрики. Более просто обстоит дело в случае, когда ковариационные матрицы одинаковы для всех К классов: C_k= C_s=C. Уравнение (31) тогда принимает следующий вид:

d_ks(x)= ln 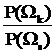+x^TC^-1(m_k-m_s)-(1/2)(m_k+m_s) ^TC^-1(m_k-m_s)=0. (32)

 

То есть при  C_k=C_s=C, m_k¹m_s гиперквадрики превращаются в линейные разделяющие функции, что подтверждает ранее сделанный нами вывод о возможности применения в этом случае метода классификации по минимуму евклидова расстояния.

В случае, когда m_k=m_s,=m, C_k¹C_s, разделяющая функция принимает вид:

ln 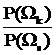+(1/2)ln 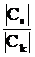-(1/2)(x-m)^T (C_k^-1-C_s^-1)(x-m)=0. (33)

 

Таким образом, можно сказать, что практическим преимуществом многомерного байесовского классификатора перед классификаторами по минимуму расстояния является возможность разделения классов, имеющих близкие средние, но разный разброс значений признаков.

Логарифм функции правдоподобия (24) представляет собой ту самую решающую функцию (19) для k-го класса, которую мы ввели в разделе 7.3. 

 

r_k(x)=lnP(W_k)+lnp(x/W_k)= lnP(W_k)+(1/2)ln|C_k|-(1/2)(x-m_k)^TC_k^-1(x-m_k). (30)

 

В соответствии с условием (19) из раздела 7.3 решение принимается в пользу того класса, для которого r_k(x) имеет максимальное значение. Отсюда название метода классификации – «максимум правдоподобия». И именно поэтому при обосновании метода часто используют так называемую «апостериорную вероятность», которая выражается через функции правдоподобия классов следующим образом:

 

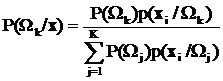.       (31)

Апостериорная вероятность интерпретируется как вероятность появления k-го класса для каждой точки с вектором координат x в пространстве яркостей [3].

Однако, поскольку величина (24) есть вероятность, принимающая значения в интервале (0,1), то логарифм ее значения есть величина отрицательная. Поэтому, как уже говорилось в разделе 7.3, решение в алгоритмах классификации принимается по значению величины, которую можно рассматривать как расстояние пикселя до класса (метрику). В данном случае такая величина есть

 

D_k(x)=ln(1/ r_k(x))=1/2(x-m_k)^TC_k^-1(x-m_k)-lnP(W_k)-(1/2)ln|C_k|.  (32)

 

 Нетрудно заметить, что в это выражение входит рассмотренное нами ранее расстояние Махаланобиса (23). Если не учитывать априорную вероятность, то есть если lnP(W_k)=0, тогда в выражении (32) остается, тем не менее, еще один член, который и определяет различие между двумя статистическими классификаторами. 

Чтобы понять, какую роль играет этот член при классификации, рассмотрим простейший вариант, когда оси эллипсоида рассеяния расположены параллельно осям координат. В этом случае |C_k|= 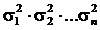, то есть последний член выражения (32) будет расти с увеличением эллипсоида рассеяния, либо по отдельным, либо по все направлениям. При этом, поскольку многозональные изображения представляются в целочисленной шкале, ln|C_k|>0.  Следовательно, во-первых, для точки с вектором координат x величина D_k(x) будет меньше расстояния Махаланобиса, во-вторых, она будет уменьшаться с увеличением эллипсоида рассеяния. Это позволяет во всех случаях более точно определять границы между классами с большой дисперсией.

Тем не менее, при классификации изображений с пространственным разрешением 15м на пиксель и хуже различия между двумя рассмотренными статистическими методами обнаружить практически невозможно [1]. Эти различия обычно проявляются при классификации сложных сцен с более высоким пространственным разрешением и большим динамическим диапазоном значений яркости.

 

7.7. Обучение статистических классификаторов. Меры статистической разделимости.

 

Методы контролируемой классификации или, иначе, классификации с обучением требуют наличия готовых обучающих данных - сигнатур классов. Обычно классификация с обучением применяется в тех случаях, когда необходимо выделить на изображении определенный набор классов, независимо от того, сколько их там на самом деле. Остальные классы могут быть отнесены либо к классу «прочее», либо объединены с другими классами, как это делается при неконтролируемой классификации.

Основой для получения сигнатур классов могут служить, в том числе, и сигнатуры, полученные при неконтролируемой классификации, или же сигнатуры, полученные в результате группировки кластеров [1]. Однако это возможно лишь в тех случаях, когда такие кластеры или их группы на изображении достаточно точно «ложатся» на определенные типы объектов. В большинстве случаев, однако, границы между сигнатурами таких классов в пространстве яркостей не оптимальны, то есть не обеспечивают минимальные ошибки при классификации всех пикселей изображения.

В разделе 7.2 был рассмотрен еще один способ получения обучающих данных, имеющийся в пакете ERDAS Imagine, - непосредственно в пространстве яркостных признаков. Однако этот способ приемлем только в тех случаях, когда между всеми парами каналов наблюдается высокая корреляция, за исключением какой-либо одной пары (обычно это пара «красный-ближний ИК»). В этом случае можно выбрать области решения на диаграмме рассеяния этой пары каналов.

Основным способом получения обучающих данных является создание сигнатур по оконтуренным на изображении эталонным участкам. При этом необходимо учитывать, что качество обучения зависит от целого ряда факторов.

1. От способа RGB-синтеза изображения при выводе на экран и особенностей палитры. В процессе RGB-синтеза, так или иначе, происходит некоторая потеря информации, обусловленная самой математической моделью этой процедуры. Кроме того, индивидуальные особенности восприятия каждым человеком цветовой гаммы влияют на способность аналитика различать объекты исследования и, следовательно, на процесс формирования обучающих выборок. Из этих соображений, особенно при большом количестве каналов, бывает полезно использовать для выбора эталонных участков RGB-композиции в главных компонентах (см. раздел 6.3).

2. От достоверности наземных данных, в том числе от способа их сбора и точности координатной привязки тестовых участков к изображению. При разрешении цифрового изображения на местности 10-15 м, а тем более 30-50м, мы едва ли сможем строго привязать точечные измерения. Следовательно, для надежного обучения классификатора необходимы тестовые участки с высокой степенью пространственной однородности.

При работе с материалами наземных обследований это еще один довод в пользу двухэтапной схемы обработки. Сначала выполняется неконтролируемая классификация с целью выбора участков, однородных по индексу определенного класса и тематическая интерпретация этих классов с использованием справочных картографических материалов и данных наземных обследований. Затем выполняется классификация с обучением по наиболее типичным однородным эталонам.

В ERDAS Imagine предусмотрен еще один способ получения наиболее однородных по яркостным признакам эталонных участков: наращивание областей с использованием функции Seed PropertiesAOI-инструментария. Этот способ рассмотрен в методическом пособии для практических занятий [1].

3. От размера и способа расположения обучающих выборок на изображении. Изменчивость спектральных отражательных свойств объектов земной поверхности даже в пределах одного изображения может оказаться очень высокой. Кроме факторов, обусловленных условиями съемки и учитывающихся в процессе нормализации изображений, на отражательные характеристики объектов могут повлиять такие факторы, как ветер, осадки и т.п. Поэтому, если не удается выбрать достаточно большой эталонный участок (обычно не менее 100 пикселей), нужно выбрать несколько эталонов одного класса в разных частях изображения и затем объединить сигнатуры этих участков в сигнатуру одного класса. При этом следует стремиться к тому, чтобы все обучающие выборки имели примерно одинаковый размер.

    

После подготовки обучающих данных необходимо провести их статистический анализ для выбора наиболее подходящего метода (или схемы) классификации. Если мы собираемся использовать параметрические методы классификации, необходимо убедиться, что гистограммы сигнатур классов могут быть аппроксимированы нормальным распределением. Последствия несоответствия распределения сигнатур нормальному рассмотрены в пособии для практических занятий [1]. Если добиться такого соответствия невозможно, лучше использовать комбинированную схему обработки с непараметрическим методом классификации в качестве основного (см. раздел 7.8.).

    Предположим теперь, что мы получили вполне надежные обучающие выборки и рассчитали параметры функций плотности распределения для всех классов. Каким способом можно оценить возможности удовлетворительной классификации конкретных данных при выбранных описаниях классов, то есть ожидаемые вероятности ошибок? Для этой цели используется такое понятие, какстатистическая разделимость.

    Статистическая разделимость классов - это некоторая функциональная характеристика, известным образом связанная с вероятностью ошибки классификации.

Как мы уже видели при рассмотрении статистических классификаторов, вероятность ошибки при разделении пары классов связана с площадью перекрытия их функций плотности распределения (рис.29).

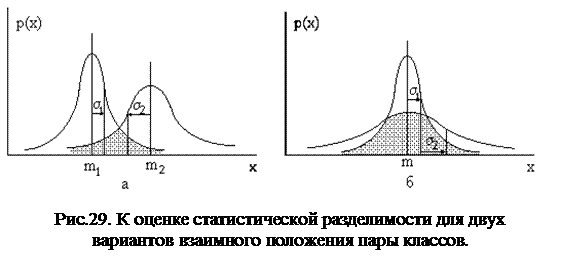    Ясно, что при различных средних значениях m₁ и m₂ (рис. 29, а) вероятность ошибки убывает при увеличении расстояния между m₁ и m₂ . Поэтому для классов с различными средними можно использовать такую меру статистической разделимости, как нормализованное расстояние:

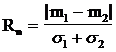. (33)

    Величина R_n связана обратной зависимостью с вероятностью ошибок: она возрастает как с увеличением расстояния между средними, так и с уменьшением дисперсии внутри классов. Для нормальных распределений эта величина принимает значение R_n=1 “на уровне одного s”, то есть когда функции плотности распределения соприкасаются в точках перегиба: |m₁-m₂|=s₁+s₂. На этом уровне при равных априорных вероятностях появления классов вероятность ошибок классификации (заштрихованная площадь) e»0.33. Это обычно считается верхней границей допустимой величины ошибки, то есть результат уже поддается интерпретации и постклассификационной обработке.

    Для многомерного случая (при C₁= C₂=C, m₁¹m₂) иногда используется квадратичное расстояние Махаланобиса между векторами средних значений [6], которое для нормальных распределений иначе называют расстоянием между плотностями распределения:

 

R₁₂=(m₁-m₂) ^TC^-1(m₁-m₂). (34)

 

Расстояние (34) также обратно пропорционально ожидаемой величине ошибки.

    Недостатки мер такого типа проявляются в случаях, когда средние значения для двух классов совпадают (рис.29, б). Поэтому для обработки всех ситуаций необходима мера более универсальная. Таковой является, например, попарная дивергенция, позволяющая учесть соотношения между значениями плотностей распределения двух классов в каждой точке х.

    Дивергенция определяется через так называемое среднее количество различающей информации.

    Средним количеством различающей информации для класса W₁ относительно класса W₂ называется величина [6]

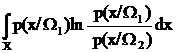. (35)

    Аналогично можно записать среднее количество различающей информации для класса W₂ относительно класса W₁. Тогда полное среднее количество различающей информации для пары классов W₁ и W₂  будет выглядеть так:

 

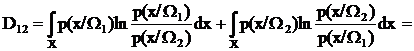
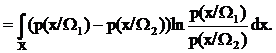(36)

Величина D₁₂ называется дивергенцией. Как видно из формулы (36), дивергенция включает само отношение правдоподобия и его логарифм, то есть учитывает расстояние между функциями правдоподобия в каждой точке пространства Х и их соотношение.

Несмотря на кажущуюся сложность выражения (36) для многомерного случая, для нормально распределенных значений х дивергенция достаточно просто вычисляется через средние и и ковариационные матрицы пары классов [4].

 

D₁₂= ½ tr [(C₁-C₂)(C₂^-1-C₁^-1)]+ ½ tr [(C₁^-1+C₂^-1)(m₁-m₂)(m₁-m₂)^T. (37)

        

Дивергенция пригодна для оценки обеих ситуаций, представленных на рис. 27. Она удовлетворяет требованиям метрики: D_ij>0 при i¹j, D_ij=0 при i=j, D_ij=D_ji, D_ij(x₁, …, x_n)£D_ij(x₁, …, x_n,x_n+1), то есть добавление нового измерения никогда не приводит к уменьшению дивергенции. Более того, если признаки классов распределены по нормальному закону с равными ковариационными матрицами, то нетрудно показать, что D_ij=R_ij, где R_ij – квадратичное расстояние Махаланобиса. При статистической независимости измерений дивергенция аддитивна: 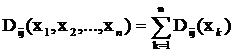. Эти свойства дивергенции иногда используют при выборе признаков для оценки их информативности [4]: при заданном количестве классов из возможного набора признаков следует отбирать те, для которых общая или средняя попарная дивергенция максимальна.  

Однако квадратичная мера D с увеличением расстояния между классами растет значительно быстрее, чем величина R из (33). Поэтому использование для набора из К классов такой оценки, как средняя попарная дивергенция, целесообразно только в тех случаях, когда все классы распределены равномерно по пространству Х. В противном случае даже один класс, далеко отстоящий от всех остальных, может дать слишком оптимистическую оценку ошибки.

В общем случае предпочтительнее использовать предлагаемую в ERDAS Imagine трансформированную дивергенцию [7], которая рассчитывается по формуле:

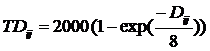.           (38)

 

Эта величина принимает при 100% точности классификации максимальное значение 2000.

    Более грубой, но и более простой оценкой является так называемое расстояние Джеффриса-Матуситы (J-M расстояние) [2]. J-M расстояние рассчитывается по формуле:

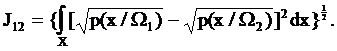(39)

Для нормально распределенных значений признака J-M расстояние вычисляется по формуле [7]:

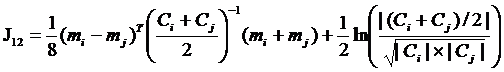. (40)

 

J-M расстояние  связано с ожидаемой вероятностью правильного распознавания зависимостью, которую можно считать почти линейной. В ERDAS Imagine при 100% вероятности правильного распознавания эта величина принимает значение 1414.

 

---

Дата добавления: 2018-05-12; просмотров: 1466; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!