Тождественно истинна (то есть принимает значение 1 при всех вещественных значениях переменной x). Какую наименьшую длину может иметь отрезок A?
Решение:
10) заметим, что здесь два условия объединяются с помощью логической операции «И»:
(x Î A) ®(x2£ 64)
(x2£ 25) ® (x Î A)
11) рассмотрим первое условие; чтобы импликация была истинна, при истинной левой части (посылке) вторая часть (следствие) тоже должна быть истинна
12) это значит, что если x принадлежит отрезку A, должно выполняться условие x2£ 64, то есть
| x |£ 8, поэтому отрезок A должен целиком содержаться внутри отрезка [–8; 8]
13) теперь рассмотрим второе условие: если x2£ 25, то есть если | x |£ 5, то такой x должен принадлежать отрезку A
14) это значит, что весь отрезок [–5; 5] должен находиться внутри A, длина этого отрезка – 10.
15) Ответ: 10.
Ещё пример задания:
Р-26 (демо-2018). Для какого наибольшего целого числа А формула
( (x £ 9) ®(x×x £ A) ) Ù ( (y×y £ A) ® (y £ 9) )
Тождественно истинна (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Решение:
1) заметим, что здесь два условия, которые объединяются с помощью логической операции «И»:
(x £ 9) ®(x×x £ A)
(y×y £ A) ® (y £ 9)
2) необходимо, чтобы оба условия были выполнены одновременно; к счастью, первое зависит только от переменной x, а второе – только от переменной y, поэтому их можно рассматривать отдельно: каждое из них задает некоторое ограничение на значение A
3) рассмотрим первое условие: (x £ 9) ®(x×x £ A). Для того чтобы импликация была истинной, нужно не допустить варианта 1 ® 0, то есть при истинной левой части правая часть тоже должна быть истинной.
|
|
|
4) это значит, что для всех 0 £ x £ 9 мы должны обеспечить x×x £ A, то есть выбрать A ³ x×x для все допустимых значений x. Очевидно, что для этого необходимо и достаточно выбрать A ³9×9= 81. Таким образом, мы определили минимальное допустимое значение A = 81.
5) теперь рассмотрим второе условие: (y×y £ A) ® (y £ 9). Чтобы оно было истинно, нужно не допустить варианта 1 ® 0. Выбором A мы можем влиять на левую часть, но не на правую. «Угрозу» представляет вариант, когда правая часть ложна, то есть y > 9. В этом случае нам нужно сделать левую часть ложной, то есть обеспечить выполнение условия y×y > A.
6) для выбора максимального A возьмем минимальное значение y, для которого y > 9. Это даёт условие 10×10> A, откуда следует A < 100
7) таким образом, максимально допустимое значение A равно 99.
8) Ответ: 99.
Решение (через отрезки, А.Н. Евтеев, Тульская обл.):
1) Если заменить неравенства буквами, то формула в общем виде будет выглядеть так:
( P ®Q ) Ù (R ® S)=1
2) Перейдём от импликаций в скобках к логическому сложению, получим:
(P +Q ) Ù (R + S)=1
3) Поскольку между скобками мы имеем логическое умножение, истинное лишь при истинности обоих сомножителей, можем перейти к системе:
|
|
|
P +Q =1
R + S=1
4) Вернёмся от букв к исходным неравенствам, учитывая инверсию:
(x > 9) + (x×x £ A)=1
(y×y > A) + (y £ 9) =1
5) Перейдём к числовой прямой. Чтобы формула была истинной, каждая записанная выше сумма должна закрывать всю ось. Для первого выражения это будет выглядеть так:
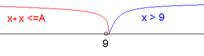
6) Интервал от 10 и далее закрывает неравенство x > 9, а интервал от 0 до 9 включительно закрывает неравенство x×x £ A. И поскольку х на этом интервале не превышает 9, выражение x×x £ A будет истинным уже при А=81
7) Аналогично для второй суммы:
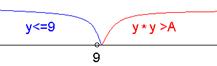
8) Интервал от 0 до 9 включительно закрывает неравенство y £ 9, а интервал от 10 и далее закроет неравенство y×y > A. И поскольку значения у начнутся здесь с 10, а y×y =100, то выражение гарантированно будет истинным, если А будет меньше 100, то есть, не будет превышать 99.
9) Ответ: 99.
Решение (графическое, О.В. Алимова):
1) Перейдем к системе и избавимся от импликации
 (x > 9) + (x×x £ A) = 1
(x > 9) + (x×x £ A) = 1
(y×y > A) + (y £ 9) = 1
2) Так как уравнения независимы, то можно рассматривать их отдельно. Согласно условию нас будет интересовать только I четверть.
3) Построим множества, удовлетворяющие первому уравнению.
|
|
|
a. дизъюнкция – объединение множеств
b. от y в первом уравнении ничего не зависит, то есть, если для какого-то x неравенство выполнилось, то оно будет выполняться для этого x при любом y, следовательно можем рассматривать области плоскости, а не только отрезки/интервалы на оси OX
c. для точек правой границы левого прямоугольника условие x2 ≤ A выполняется
d. для точек левой границы правого прямоугольника условие x > 9 не выполняется
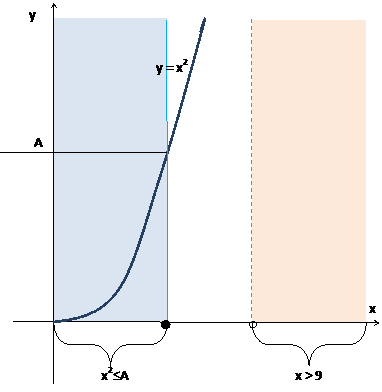
4) При увеличении значения А, ширина левого прямоугольника будет увеличиваться, и при А = 81, объединение прямоугольников закроет все значения х. Это наименьшее возможное значение А. При дальнейшем увеличении А, будет расти область пересечения прямоугольников, но все значения х, будут входить в объединение прямоугольников.
5) Рассмотрим второе уравнение. Множества удовлетворяющие этому уравнению будут выглядеть так:
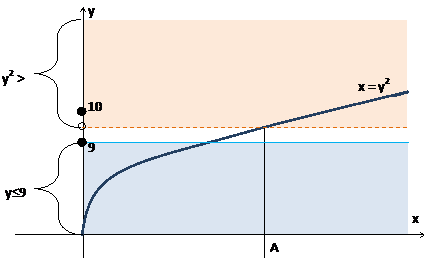
6) Пока верхний и нижний прямоугольник пересекаются, можем увеличивать А.
7) Значение А можно увеличивать и дальше, пока в область объединения прямоугольников не перестанет попадать целое значение y. А это произойдет при А=100, для у=10 неравенство y2 > A перестанет выполняться. Наибольшее значение А=99.
|
|
|
8) Ответ: 99.
9) Замечания. В зависимости от строгости(не строгости) неравенств в исходном уравнении, будут включатся или исключатся точки, лежащие на границе соответствующей области.
Так значение А для уравнения (x < 9) ® (x×x £ A) = 1 будет 64,
для уравнения (x < 9) ® (x×x < A) = 1 будет 65,
а для уравнения (x £ 9) ® (x×x < A) = 1 будет 82. Аналогично, во втором уравнении, могут получиться числа 100, 81, 80.
Решение (М.В. Кузнецова):
1) Заметим, что данная формула содержит конъюнкцию двух импликаций. Конъюнкция истинна только, если оба операнда равны 1, т.е. обе импликации должны быть равны 1, для этого надо исключить ситуации 1 ®0 , переведя их к истинным импликациям 1® 1 или 0 ® 0.
2) Дальнейшие рассуждения оформим в таблице.
| Формула* | ( (x £ 9 ) ®( A≥ x×x) ) Ù ( ( A≥ y×y) ® ( y £ 9 ) ) | |||
| Изменяемое выражение** | - | + | + | - |
| Нельзя допустить | 1 | 0 | 1 | 0 |
| Надо обеспечить | 1 | 1 | 0 | 0 |
| Новые выражения | x £9, x ϵ[0;9] | A ≥ x∙x | A < y∙y | y > 9, y ϵ [10; ∞) |
| Выводы | A ≥ 9∙9, Amin = 81 | A<10∙10, A max= 99 | ||
Пояснения
* При переписывании формулы в неравенствах с «А» меняем местами левую и правую часть, т.е. «А» пишем слева.
** Помечаем символом «+» элементы формулы, содержащие «A», изменяя значения которых должны исключить неблагоприятные ситуации.
3) Ответ: 99.
Ещё пример задания:
Р-25. Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число a, такое что выражение
( x &125¹ 1) Ú ((x & 34 = 2) ® (x & a = 0))
Дата добавления: 2018-05-12; просмотров: 982; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
