Как вычислять выражение с поразрядными операциями

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

В задачах ЕГЭ до настоящего времени использовалась только поразрядная логическая операция «И» (она обозначается символом &), которая выполняется между соответствующими битами двоичной записи двух целых чисел. Не забывайте, что

Результат поразрядной операции между целыми числами – это целое число!.

Например, найдём результат поразрядной операции 29 & 11:

29 = 11101₂

11 = 01011₂

9 = 01001₂

Серым фоном отмечены биты, которые в обоих числах равны 1. Только они и будут равны 1 в числе-результате. Таким образом, 29 & 11 = 9.

Теперь найдём результат операции (29 & 11 = 0). Не забывайте, что

Результаты операций (a & b = 0) и (a & b ¹ 0) – это логические значения (истина/ложь)!.

Вычислим значение выражения:

( (x & 26 = 0) Ú (x & 13 = 0)) ® ((x & 78 ¹ 0) ® (x & A = 0))

при x = 5, A = 57:

( (5 & 26 = 0) Ú (5 & 13 = 0)) ® ((5 & 78 ¹ 0) ® (5 & 57 = 0))

Вычисляем результаты поразрядного И (это числа!):

5 & 26 = 0 5 & 13 = 5
5 & 78 = 4 5 & 57 = 1

Теперь вычисляем логические значения (И – истина, Л – ложь):

(5 & 26 = 0) = И (5 & 13 = 0) = Л
(5 & 78 ¹ 0) = И (5 & 57 = 0) = Л

Наконец, подставляем эти логические значения в заданное выражение:

(И Ú Л) ® (И ® Л)
И ® Л = Л

При заданных условиях выражение ложно.

Решение задач с поразрядными операциями

Для решения этих задач удобно применять метод, предложенный А.В. Здвижковой (г. Армавир) и обоснованный автором[2]. Введём обозначения

Это означает, что если истинно 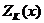, то это равносильно тому, что истинно . Для сокращения записи вместо 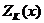будем писать просто .

Пусть в двоичной записи числа K бит с номером i, обозначаемый как k_i, равен 1. Если при этом для некоторого x выполнено условие , то соответствующий i-й бит в двоичной записи числа x равен нулю, так как должно выполняться условие .

Для преобразования выражений полезно следующее свойство:

где «or» означает поразрядную дизъюнкцию между двумя натуральными числами. Для доказательства предположим, что в двоичной записи числа K биты с номерами i₁, i₂, …, i_q равны 1, а остальные равны 0; а в двоичной записи числа M биты с номерами j₁, j₂, …, j_p равны 1, а остальные равны 0. Истинность выражения в левой части означает, что все биты числа x, входящие во множества B_K = {i₁, i₂, …, i_q} и B_M = {j₁, j₂, …, j_p} одновременно равны нулю. Поэтому любая комбинация битов из этих множеств тоже равна нулю. Это справедливо, в том числе, и для множества, которое представляет собой объединение множеств B_K и B_M, то есть, для множества единичных битов числа K or M.

Самый важный результат можно сформулировать так:

Условие истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

Доказательство. Пусть в двоичной записи числа K биты с номерами i₁, i₂, …, i_q равны 1, а остальные равны 0. Пусть также истинно для некоторого x, это значит, что в числе x биты с теми же номерами – нулевые. Если все единичные биты двоичной записи числа M входят во множество B_K = {i₁, i₂, …, i_q}, то истинно и высказывание , а следовательно – высказывание (1 ® 1 = 1). Если же хотя бы один бит двоичной записи числа M не входит во множество B_K (пусть это будет бит с номером j), то для тех х, у которых все биты из множества B_K нулевые, а бит j равен 1, выполняется , но не выполняется , так что высказывание ложно.

Для упрощения выражений полезен следующий результат:

Условие при любых натуральных K, M и N ложно для некоторых натуральных значений x.

Идея доказательства состоит в том, чтобы представить импликацию в виде произведения двух импликаций:

Вторая импликация в правой части ложна хотя бы для некоторых x, поскольку из того, что некоторые биты числа x равны нулю (выполняется ) совершенно не следует, что какие-то другие (или те же самые) биты того же числа ненулевые (выполняется ). Строгое доказательство дано в статье, ссылка на которую приведена в сноске на предыдущей странице.

Метод, предложенный А.В. Здвижковой заключается в следующем:

1) упростить заданное выражение, сведя его к импликации, в которой нет инверсий

2) применить полученные выше результаты для нахождения всех подходящих значений неизвестного числа a, включая минимальное и максимальное значения.

Этот же метод можно применить и в том случае, когда результат поразрядной операции «И» сравнивается не с нулём, а с другими числами. Например, рассмотрим выражение R = (x &125 = 5). Переведём числа в двоичную систему:

6 5 4 3 2 1 0

125 = 1111101₂

5 = 101₂.

Истинность R означает, что

1) биты числа x с номерами 3, 4, 5 и 6 равны 0;

2) биты числа x с номерами 0 и 2 равны 1.

С учётом введённых выше обозначений можно записать эквивалентное условие:

R = (x &125 = 5) Û .

Применяя операцию «НЕ» к этому выражению, получаем

= (x &125 ¹ 5) Û Û .

В общем виде для чисел b и c, таких, что множество единичных битов числа c входит во множество единичных битов числа b, имеем

R = (x & b = c) Û

= (x & b ¹ c) Û .

где c₁, c₂, …, c_q – степени числа 2, которые соответствуют единичным битам числа c. Например, для
c = 5 = 101₂ имеем c₁ = 2² = 4, c₂ = 2⁰ = 1.

Пример задания:

Р-28. На числовой прямой даны отрезки A = [70; 90], B = [40; 60] и C = [0; N] и функция

F(x) = (Ø (x Î A) ®(x Î B) ) Ù (Ø (x Î C) ® (x Î A) )

При каком наименьшем числе N функция F(x) истинна более чем для 30 целых чисел x?

Решение:

1) для сокращения записи введём обозначения

A = (x Î A), B = (x Î B), C = (x Î C).

фактически A(x) – это логическая функция, определяющая принадлежность числа x отрезку A

2) запишем функцию в виде:

3) используя распределительный закон логики, упрощаем:

4) это значит, что функция истинна на всём отрезке A (там 21 целое число) и на общей части отрезков B и C, где должно быть не менее 31 – 21 = 10 целых чисел

5) нарисуем отрезки на числовой оси:

6) по рисунку видно, что

а) при N < 40 отрезки B и C не имеют общей части

б) при N Î [40; 60] общая части отрезков B и C – это отрезок [40; N], на нём расположены
N – 40 + 1 целых чисел

в) при N > 60 общая части отрезков B и C совпадает с отрезком B, ему принадлежит 21 целое число

7) таким образом, функция F(x) может быть истинной не более чем для 42 целых чисел

8) если требуется обеспечить её истинность для 31 целого числа, нужно выбрать N из условия

N – 40 + 1 = 10, откуда N = 49

9) Ответ: 49.

Ещё пример задания:

Р-27. Известно, что для некоторого отрезка А формула

( (x Î A) ®(x²£ 64) ) Ù ( (x²£ 25) ® (x Î A) )

Дата добавления: 2018-05-12; просмотров: 3752; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!