Где С- окружность радиуса 2 с центром в точке 3i.
Решение: Функция 
аналитична внутри круга 
, ограниченного окружностью С, 
. Тогда по интегральной формуле Коши получим
= 
.
Ответ: .
Варианты контрольной работы
Вариант №1
1. Вычислить повторный интеграл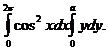 
2. Вычислить двойной интеграл 
, где D – область, ограниченная линиями xу=1, x=2, у= 
.
3.Вычислить площадь фигуры, ограниченной линиями: 
.
4.Расставить пределы интегрирования в тройном интеграле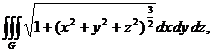 
где G есть сфера 
. Вычислить.
5. Вычислить 
, где ОА – отрезок прямой; О(0; 0), А(2; 1).
6*. Вычислить объем тела V, ограниченного поверхностями 
с помощью двойного интеграла.
7. вычислить 
8. Найти 
9. Вычислить 
Вариант №2.
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
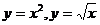
3. Найти площадь, ограниченную кривыми 
4. Расставить пределы интегрирования в тройном интеграле 
, где V ограничена плоскостями х=0,у=0, z=0 и частью сферы 
в первом октанте. Вычислить.
5. Вычислить по формуле Грина: 
, где С: х 2 + у 2 = 4.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить 
8. Найти 
9. Вычислить 
Вариант№3
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
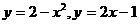
3. Найти площадь, ограниченную кривыми 
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
Вычислить.
5. Преобразовать с помощью формулы Грина
.
|
|
|
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить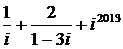 
8. Найти 
9. Вычислить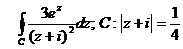 
Вариант№4
1. Вычислить повторный интеграл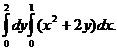 
2. Вычислить , где D – область, ограниченная линиями xу=1, x=2, у= .
3. Найти площадь, ограниченную кривыми 
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
Вычислить.
5. Вычислить 
, где А (0;0), В (π;2π), т.е. линия интегрирования отрезок АВ от А к В.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить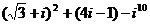 
8. Найти 
9. Вычислить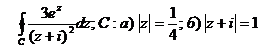 
Вариант №5
1. Вычислить повторный интеграл 
2. Вычислить 
, где D – область, ограниченная линиями x=0, x= 
, у=2.
3. Вычислить площадь фигуры, ограниченной линиями:
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
Вычислить.
5. Вычислить по формуле Грина: 
, где С: у = х; х = 2; у = 0.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить 
8. Найти 
9. Вычислить 
Вариант №6
1. Вычислить повторный интеграл 
2. Вычислить 
, где D – область, ограниченная прямыми x=0, x=4, у=1, у=е.
3. Переходя к полярным координатам, найти площадь, ограниченную линиями: 
.
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V есть тело, ограничен поверхностями 
. Вычислить .
|
|
|
5. Вычислить криволинейный интеграл 
вдоль линии у = 2x при 0≤х≤1
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить 
8. Найти 
9. Вычислить 
Вариант №7
1.Вычислить повторный интеграл, переходя к полярным координатам: 
2. Вычислить 
, где D – область, ограниченная линиями x-2у=0, x-у=0, х=4.
3. Вычислить площадь фигуры, ограниченной линиями: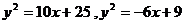 
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
Вычислить.
5. Вычислить по формуле Грина: , где С: х 2 + у 2 = 16.
6*.Вычислить объем тела, ограниченного поверхностями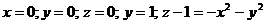 
7. Вычислить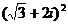 
8. Найти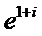 
9. Вычислить 
Вариант№8
1. Вычислить повторный интеграл, переходя к полярным координатам:
2. Вычислить двойной интеграл 
, где областьD ограничена кривой 
и осью ОХ.
3. Вычислить площадь фигуры, ограниченной линиями: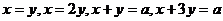 
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями 
. Вычислить.
5. Вычислить криволинейный интеграл 
вдоль линии у = x при 0≤х≤1
6*. Вычислить объем тела, ограниченного поверхностями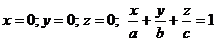 
|
|
|
7. Вычислить 
8. Найти 
9. Вычислить 
Вариант №9.
1. Вычислить повторный интеграл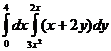 
2. Вычислить 
, где область D ограничена линиями 
3. Вычислить площадь фигуры, ограниченной линиями: 
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
. Вычислить.
5. Вычислить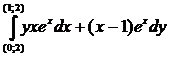 
6*. Вычислить объем тела, ограниченного поверхностями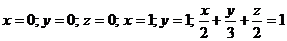 
.
7. Вычислить 
8. Найти 
9. Вычислить 
Вариант№10.
1. Вычислить повторный интеграл, переходя к полярным координатам 
2. Переходя к полярным координатам, вычислить двойной интеграл 
, где D – область, ограниченная окружностью 
3. Вычислить площадь фигуры, ограниченной линиями:
4. Расставить пределы интегрирования в тройном интеграле 
, где V ограничена плоскостью z=1 и параболоидом 
. Вычислить.
5. Вычислить по формуле Грина: , где С: х 2 + у 2 = 36.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить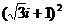 
8. Найти 
9. Вычислить 
Вариант № 11
1. Вычислить повторный интеграл
2. Переходя к полярным координатам, вычислить двойной интеграл , где D – область, ограниченная окружностью 
3. Вычислить площадь фигуры, ограниченной линиями:
|
|
|
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
Вычислить
5. Вычислить криволинейный интеграл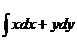 
вдоль линии у = x при 0≤х≤1
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить 
8. Найти 
если 
9. Вычислить 
Вариант № 12
1. Вычислить повторный интеграл 
2. Переходя к полярным координатам, вычислить двойной интеграл 
, где D – полукруг диаметра а с центром в точке С(а/2;0) в верхней полуплоскости.
3. Вычислить площадь фигуры, ограниченной линиями: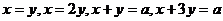
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями 
. Вычислить
5.Вычислить криволинейный интеграл 1-го рода 
, где 
.
6*. Вычислить объем тела, ограниченного поверхностями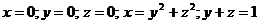 
7. Вычислить 
8. Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант № 13
1. Вычислить повторный интеграл
2. Вычислить 
, если D ограничена линиями: 
.
3. Вычислить площадь фигуры, ограниченной линиями: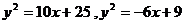
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V есть параллелепипед: 
. Вычислить.
5.Вычислить криволинейный интеграл 2-го рода
, 
6*.Вычислить объем тела, ограниченного поверхностями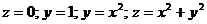 
7. Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант №14
1. Вычислить повторный интеграл, переходя к полярным координатам 
2. Вычислить 
, если D ограничена линиями: 
.
3. Вычислить площадь фигуры, ограниченной линиями:
4. Расставить пределы интегрирования в тройном интеграле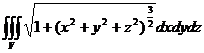 
, если тело V ограничено поверхностью 
Вычислить.
5.Вычислить по формуле Грина: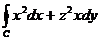 
, где С: х 2 + z 2 = 16.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант №15
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: .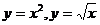
3. Переходя к полярным координатам, найти площадь, ограниченную линиями: .
4. а) Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями 
б) Вычислить.
5.Вычислить криволинейный интеграл 2-го рода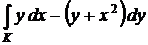
, где К – дуга параболы 
над осью ОХ по часовой стрелке.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант № 16
1. Вычислить повторный интеграл 
2. Вычислить , если D ограничена линиями: 
3. Найти площадь, ограниченную кривыми
4. Расставить пределы интегрирования в тройном интеграле , где V ограничена плоскостями х=0,у=0, z=0 и частью сферы в первом октанте. Вычислить.
5. Вычислить криволинейный интеграл 
вдоль линии у = 2 x при 0≤х≤2
6*. Вычислить объем тела, ограниченного поверхностями 
7. Дано: 
Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
9.Вычислить 
Вариант № 17
1. Вычислить повторный интеграл, переходя к полярным координатам
2. Вычислить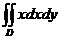 
, если областьD удовлетворяет неравенствам: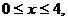 
.
3.Найти площадь, ограниченную кривыми
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V ограничено поверхностями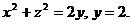 
Вычислить.
5. Вычислить криволинейный интеграл 2-го рода 
, где С – окружность х2 + у2 = 1.
6*. Вычислить объем тела, ограниченного поверхностями 
7.Дано: 
Вычислить 
8.. Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант № 18
2. Вычислить 
, если область D задана неравенствами: 
.
3. Найти площадь, ограниченную кривыми
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями Вычислить.
5.Вычислить криволинейный интеграл 2-го рода
, где АВ – отрезок прямой, А(1, 1), В(3, 4).
6*. Вычислить объем тела, ограниченного поверхностями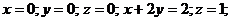 
7.Дано: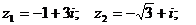 
Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант № 19
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
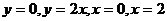
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V есть шар радиуса R. Вычислить.
5. Вычислить криволинейный интеграл 
, где l -отрезок прямой х = t +1, y = 2t +1, z = 3t +1 от точки А (1;1;1) до В (2;3;4).
6*. Вычислить объем тела, расположенного в первом октанте и ограниченного поверхностями: 
.
7. Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант №20
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
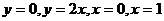
3.Вычислить площадь фигуры, ограниченной кривыми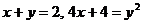 
4. Расставить пределы интегрирования в тройном интеграле 
, если тело V есть шар радиуса R. Вычислить.
5. Вычислить криволинейный интеграл: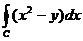 
, где С – контур треугольника, образованного осями координат и прямой 
(обход против часовой стрелки).
6*. Вычислить объем тела, ограниченного поверхностями 
.
7. Дано: 
Вычислить
8.. Выделить вещественную и мнимую часть функции, подставив вместо z: 
.
9.Вычислить
Вариант №21
1. Вычислить повторный интеграл 
2. Вычислить 
, если D: 
.
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле , если тело V есть параллелепипед: . Вычислить.
5. Вычислить криволинейный интеграл 
, где L – дуга кривой у = х 2 от точки А (1;1) до В (2;4).
6*. Вычислить объем тела, ограниченного поверхностями 
.
7. Дано: 
Вычислить 
8.. Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить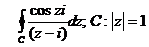 
Вариант №22
1. Вычислить повторный интеграл 
2. Вычислить 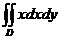, если D ограничена линиями: 
.
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле 
, где тело V ограничено поверхностями Вычислить.
5. Вычислить криволинейный интеграл , где L – дуга параболы х = у 2 от точки А (1;1) до В (25;5).
6*. Вычислить объем тела, ограниченного поверхностями 
.
7. Дано: Вычислить 
8. . Выделить вещественную и мнимую часть функции, подставив вместо z: 
Найти 
9. Вычислить 
Вариант №23
1. Вычислить повторный интеграл 
2.Вычислить 
, если D ограничена линиями: 
3.Вычислить площадь фигуры, ограниченной кривыми 
(ближайшей от начала координат фигуры)
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями .
5. Вычислить криволинейный интеграл: 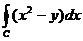, где С – прямоугольник, образованный прямыми: х = 0, х = 1, у = 0, у = 2.
6*. Вычислить объем тела, ограниченного поверхностями 
7. Дано: 
Вычислить
8.Проверить аналитичность функции 
Найти
9. Вычислить 
Вариант №24
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями Вычислить.
5. 
, где С – верхняя половина эллипса 
, 
, пробегаемая по ходу часовой стрелки.
6*.Вычислить объем тела, ограниченного поверхностями
7. Дано: 
Вычислить
8. Выделить вещественную и мнимую часть функции, подставив вместо z: 
9. Вычислить 
Вариант №25
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями . Вычислить.
5. Вычислить криволинейный интеграл 
, где l -отрезок прямой y = kx от точки А (0;0) до В (2;6).
6*. Вычислить объем тела, ограниченного поверхностями .
7. Решить уравнение 
8.Вычислить значение функци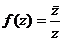и 
при 
9.Вычислить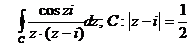 
Вариант №26
1. Вычислить повторный интеграл 
2. Вычислить 
, если D ограничена линиями: 
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями 
Вычислить.
5. Вычислить криволинейный интеграл 2-го рода 
, где С – верхняя половина эллипса 
, 
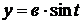, пробегаемая по ходу часовой стрелки.
6*. Найти объем тела V, ограниченного поверхностями с помощью двойного интеграла.
7. Решить уравнение 
8. Вычислить значение функции 
при
9.Вычислить 
Вариант №27.
1. Вычислить повторный интеграл 
2. Вычислить 
, где D – четверть круга 
лежащая в первой координатной четверти.
3.Вычислить площадь меньшей из фигур, ограниченных кривыми 
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями Вычислить.
5. Вычислить криволинейный интеграл 
вдоль линии у = ln x от точки А (1;0) до В (е;1).
6*. Вычислить объем тела, ограниченного поверхностями .
7.Решить уравнение 
8. Вычислить значение функци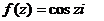и 
при 
9.Вычислить 
Вариант №28
1. Вычислить повторный интеграл 
2. Вычислить 
, где D – область, определяемая неравенствами: 
.
3.Вычислить площадь фигуры, ограниченной кривыми 
4. Расставить пределы интегрирования в тройном интеграле , если тело V есть тело, ограничен поверхностями . Вычислить.
5. Вычислить криволинейный интеграл 
, где АВ – дуга кривой у = х 2 от точки А (-1;1) до В (1;1).
6*. Вычислить объем тела, ограниченного поверхностями .
7. Вычислить 
при 
8. Вычислить значение функции 
при 
9. Вычислить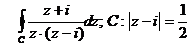 
Вариант №29
1. Вычислить повторный интеграл 
2. Вычислить , где областьD ограничена кривой и осью ОХ.
3.Вычислить площадь фигуры, ограниченной кривыми 
(в 1-ой координатной четверти).
4. Расставить пределы интегрирования в тройном интеграле , если тело V ограничено поверхностями Вычислить.
5. Вычислить криволинейный интеграл 
вдоль линии у = x при 0≤х≤2
6*. Вычислить объем тела, расположенного в первом октанте и ограниченного поверхностями: .
7. Вычислить 
при 
8. Вычислить значение функции 
при
9. Вычислить 
Дата добавления: 2018-05-12; просмотров: 333; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!