Означення дотичної, піддотичної, нормалі

Нехай функція y=f(x) диференційована в точці х_0. рівняння дотичної до графіка функції y=f(x) в цій точці має такий вигляд:

,

де х і у – біжучі координати дотичної, f ‘(x₀)=k – кутовий коефіцієнт дотичної, який дорівнює значенню похідної в точці х₀, тобто тангенс кута нахилу дотичної до доданого напрямку осі абсцис.

    Відрізок АВ, що міститься між абсцисою точки дотику і точкою перетину дотичної з віссю абсцис, називають під дотичною. Її довжина дорівнює |х₀-х₁|.

    Пряма МС, перпендикулярна до дотичної в точці її дотику М до графіка функції у=f(x), називається нормаллю.

    Рівняння нормалі записують у вигляді:

якщо f ‘(x₀) 0(в противному разі рівняння нормалі х-х₀=0).

    На цей матеріал можна скласти ряд задач. Розглянемо деякі з них.

1. Дано абсцису точки дотику х₀ графіка функції у=f(x), а необхідно записати рівняння дотичної, що проходить через точку з цією абсцисою.

Для цього знаходимо похідну функції у=f(x), її значення в точці х₀, тобто 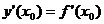, та значення функції в точці х₀, тобто . Цих даних достатньо, щоб записати рівняння дотичної .

2. Який кут утворює дотична з додатним напрямком осі абсцис, якщо відома абсциса точки дотику х₀?

    Оскільки кутовий коефіцієнт дотичної ,то .

    Таким чином, задача зводиться до знаходження похідної функції у=f(x), тобто y’=f ‘(x), і обчислення її значення в точці х₀.

    3. Знайти гострий кут між дотичними, проведеними до графіків функцій ,що мають спільну абсцису х₀:

,  .

    4. Знайти довжину дотичної до графіка функції у=f(x), абсциса точки дотику якої дорівнює х₀.

    Довжиною дотичної прийнято називати відстань між точкою дотику до графіка функції і точкою її перетину з віссю абсцис.

    У цьому випадку знаходимо

і скористаємося формулою

 

Приклади:

Приклад 1. Знайти рівняння дотичної до графіка функції

в точці з абсцисою х₀=3.

Розв’язання. Знайдемо похідну функції, значення функції та її похідної в точці х₀:

скориставшись рівнянням дотичної

,

матимемо

Звідси .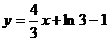

Відповідь: .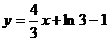

Приклад 2. Який кут з віссю абсцис утворює дотична до параболи y=x²-4x+8 в точці (3;5)?

Розв’язання. Безпосередньо підстановкою координат заданої точки в рівняння параболи переконуємося, що вона їй належить.

Знайдемо похідну y’=2x-4.

Тоді . Звідси

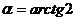
Відповідь: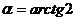

Приклад 3. Дотична до графіка функції

нахилена до осі абсцис під кутом . Знайти координати точки дотику.

Розв’язання. Знайдемо похідну функції :

.

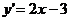За умовою y’(x₀)=tg =1 маємо

отже, дотична до параболи проходить через точку А(2;2).

Відповідь: А(2;2).

 

Розділ 2

Застосування похідної

Правила диференціювання

Теорема: Якщо функції u(x) і n(x) мають похідні у всіх точках інтервалу (a; b), то

(u(x)±(x))’ = u’(x)±n’(x)

для любого х є (a; b). Коротше,

(u±n)’ = u±n’

Доведення: Суму функцій u(x)+n(x), де х є (a; b), яка представляє собою нову функцію, позначимо через f(x) і знайдемо похідну цієї функції,

Нехай х₀ – деяка точка інтервалу (a; b).

 

 Тоді     

 

Також,

Так як

х₀ – допустима точка інтервалу (a; b), то маємо:

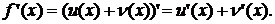
Випадок добутку розглядається аналогічно. Теорема доведена.

Наприклад,

а)

б)

в)

Зауваження. Методом математичної індукції доводиться справедливість формули (u₁(x) + u₂ (x) +… кінцевого числа складених.

Теорема. Якщо функції u(x) і n(x) мають похідні у всіх точках інтервалу (a; b), то

для любого х є (a; b). Коротше,

Доведення. Позначимо похідні 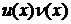через  х є (a; b), і найдемо похідну цієї функції, виходячи із визначення.

Нехай х₀ – деяка точка інтервалу (a; b). Тоді

 

Навіть так як

то

 

 

Так як х₀ – вільна точка інтервалу (a; b), то маємо

Теорема доведена.

Приклад,

а)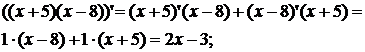

 

б)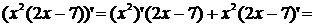

 

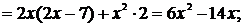
в)

 

Наслідок. Постійний множник можна виносити за знак похідної:

Доведення. Застосувавши множник можна виносити за знак теорему про похідну де а – число, отримаємо

Приклади.

а)

б)

Похідна частки двох функцій .

Теорема. Якщо функції  мають похідні у всіх точках інтервалу (a; b), причому  для любого х є (a; b), то

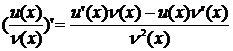
для любого х є (a; b).

Доведення. Позначимо тимчасово 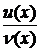 через  знайдемо використовуючи визначення похідної.

Нехай х₀ – деяка точка інтервалу (a; b).

Тоді,

 

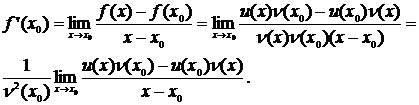
Навіть, так як

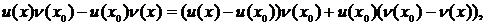 то

і послідовно

Так як х₀ – вільна точка інтервалу (a; b), то в останній формулі х₀ можна замінити на х. Теорема доведена.

Приклади.

а)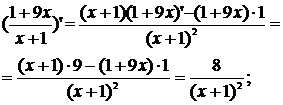  

 

б)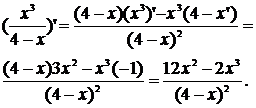

 

---

Дата добавления: 2018-05-09; просмотров: 981; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!