Тема 2. Диффузия моноэнергетических нейтронов (3 лекции).
Основное приближение модели диффузии моноэнергетических нейтронов заключается в том, что считается, что все нейтроны имеют одну и ту же энергию, то есть нейтронное поле описывается в предположении, что при взаимодействии с ядрами среды энергия нейтронов не изменяется. Это возможно в случае, если при взаимодействии нейтронов с ядрами среды идут только процессы поглощения, упругого резонансного рассеяния или потенциального рассеяния на тяжелых или жестко связанных в кристаллической решетке или молекуле ядрах среды. Это связано с тем, что при протекании всех перечисленных процессов взаимодействия нейтронов с ядрами среды энергия нейтрона не меняется.
уравнение баланса скоростей процессов в фазовом объеме:
- 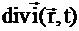 -
- 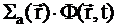 +
+ 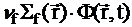 +
+ 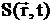 =
= 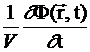 .
.
Закон Фика:

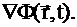
закон Фика справедлив для больших (размер среды много больше длины свободного пробега нейтрона в среде) слабопоглощающих ( 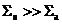 ) сред, состоящих из тяжелых (атомная масся больше 10а.е.м.) ядер, далеко (более 3-х длян свободного пробега нейтрона в среде) от локальных неоднородностей и в случае, если макроскопическое сечение рассеяния слабо зависит от пространственной переменной.
) сред, состоящих из тяжелых (атомная масся больше 10а.е.м.) ядер, далеко (более 3-х длян свободного пробега нейтрона в среде) от локальных неоднородностей и в случае, если макроскопическое сечение рассеяния слабо зависит от пространственной переменной.
Необходимо отметить, что в рамках диффузионного приближения возможно учесть слабую анизотропию потенциального рассеяния, если для определения коэффициента диффузии вместо полного макроскопического сечения использовать, так называемое, транспортное макроскопическое сечение - 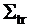 , которое рассчитывается по следующей формуле:
, которое рассчитывается по следующей формуле: 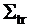 =
= 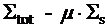 , где
, где 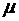 - средний косинус угла рассеяния в лабораторной системе. Если рассеяние в лабораторной системе изотропно, то средний косинус угла рассеяния равен нулю и транспортное сечение равно полному сечению. Вводится понятие коэффициента диффузии
- средний косинус угла рассеяния в лабораторной системе. Если рассеяние в лабораторной системе изотропно, то средний косинус угла рассеяния равен нулю и транспортное сечение равно полному сечению. Вводится понятие коэффициента диффузии 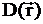 =
= 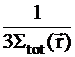 [см].
[см].
|
|
|
Таким образом, закон Фика позволяет получить т.н. уравнение диффузии моноэнергетических нейтронов
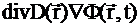 -
- 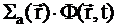 +
+ 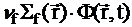 +
+ 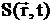 =
= 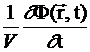
Запишем уравнение диффузии моноэнергетических нейтронов для нескольких частных случаев:
1) стационарная задача (нет зависимости от временной переменной):
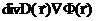 -
- 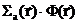 +
+ 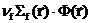 +
+ 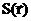 = 0;
= 0;
2) стационарная задача, среда не размножающая (сечение деления равно нулю):
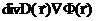 -
- 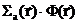 +
+ 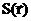 = 0;
= 0;
3) гомогенная (свойства среды не зависят от пространственной переменной) не размножающая среда, стационарная задача
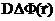 -
- 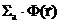 +
+ 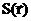 = 0.
= 0.
Поскольку в случае гомогенной среды ее свойства не зависят от пространственной переменной, следовательно, в первом слагаемом коэффициент диффузии можно вынести за знак дивергенции, а дивергенция от градиента функции - это лапласиан этой функции. Этот факт учтен в последнем уравнении. Разделим последнее уравнение на коэффициент диффузии и введем новое обозначение: 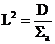 [см2]. Введенная величина называется квадратом длины диффузии нейтронов, а
[см2]. Введенная величина называется квадратом длины диффузии нейтронов, а 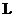 [см] - длиной диффузии нейтронов, соответственно. Перепишем последнее уравнение в виде:
[см] - длиной диффузии нейтронов, соответственно. Перепишем последнее уравнение в виде:
|
|
|
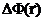 -
- 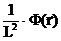 +
+ 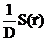 = 0.
= 0.
Решения уравнения диффузии в гомогенной бесконечной среде 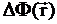 -
- 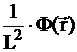 +
+ 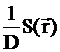 = 0. в разных геометриях:
= 0. в разных геометриях:
1. Точечный источник мощностью 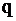 [1/с] в бесконечной, не размножающей, гомогенной среде
[1/с] в бесконечной, не размножающей, гомогенной среде
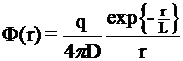
2. Плоский источник мощностью 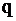 [1/(см2с)] в бесконечной, не размножающей, гомогенной среде.
[1/(см2с)] в бесконечной, не размножающей, гомогенной среде.
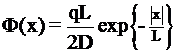
3. Нитевидный источник мощностью 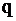 [1/(см с)] в бесконечной, не размножающей, гомогенной среде.
[1/(см с)] в бесконечной, не размножающей, гомогенной среде.
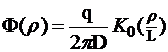
Условие для функции плотности потока нейтронов, следующие из ее определения. Эти очевидные условия отражает тот факт, что по определению функция плотности потока нейтронов не отрицательна и ограничена.
Начальное условие по времени. Это условие важно для решения нестационарного уравнения диффузии (2.6) и говорит о том, что в начальный момент времени t=0 функция плотности потока известна, например, из решения соответствующего стационарного уравнения: 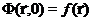 , где
, где 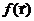 - известная функция.
- известная функция.
Условие на границе раздела сред с разными свойствами. Это условие сшивки плотности потока нейтронов на границе раздела двух сред с разными свойствами. Необходимо отметить, что при получении этого условия будет использоваться выражения для односторонних токов в области около границы раздела двух сред, поэтому погрешность решения уравнения диффузии в этой области будет высокой. В тоже же время, допуская большую погрешность решения в области около границы раздела, получаются условия для сшивки решений на границы раздела двух сред, которые гарантируют хорошую точность решения вне этой области. Рассмотрим границу раздела сред - рисунок 2.
|
|
|

СРЕДА 1 СРЕДА 2


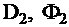

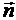

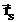
Рис. 2 Граница раздела сред с разными свойствами.
Если на линии границы нет локальных источников и поглотителей нейтронов, то количество нейтронов, которые пересекают единичную площадку, расположенную в точке 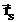 , из первой среды во вторую равно количеству нейтронов, которые влетают во вторую среду из первой через эту же площадку, и наоборот. Это значит, что выполняются следующие точные равенства:
, из первой среды во вторую равно количеству нейтронов, которые влетают во вторую среду из первой через эту же площадку, и наоборот. Это значит, что выполняются следующие точные равенства:
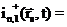
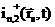 и
и 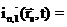
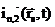 ,
,
которые отражают этот факт. Воспользуемся для односторонних токов выражениями (2.5):
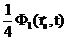 -
- 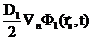 =
= 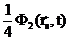 -
- 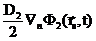 ,
,
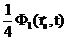 +
+ 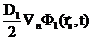 =
= 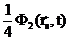 +
+ 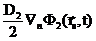 .
.
Это уже приближенные (с точностью до применимости диффузионного приближения) соотношения. После сложения этих равенств получим одно условие - 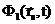 =
= 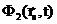 , а после вычитания - второе:
, а после вычитания - второе: 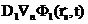 =
= 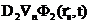 .
.
|
|
|
Таким образом, на границе раздела двух сред с разными свойствами функция плотности потока нейтронов и проекции вектора тока на нормаль непрерывны.
Условие на не вогнутой границе среда-вакуум. Рассмотрим не вогнутую границу среда-вакуум, то есть такую границу, что все нейтроны, покинувшие среду, обратно возвратиться из вакуума в среду не могут. Необходимо отметить, что при получении этого условия будет использоваться выражение для одностороннего тока в области около границы среда-вакуум, поэтому погрешность решения диффузионного уравнения в этой области будет высокой. В тоже же время, допуская большую погрешность решения в области около границы среды и вакуума, получается условие для плотности потока на этой границе, которое гарантирует хорошую точность решения внутри среды. Рассмотрим границу раздела двух сред - рисунок 3.
 СРЕДА ВАКУУМ
СРЕДА ВАКУУМ

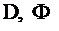



Рис. 3 Не вогнутая граница среды с вакуумом.
Раз граница среда-вакуум не вогнутая, то нет нейтронов, которые имеют направление движения из вакуума в среду, поэтому через единичную площадку, расположенную в точке 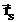 , нет тока нейтронов из вакуума в среду, то есть
, нет тока нейтронов из вакуума в среду, то есть 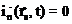 . Использование для одностороннего тока выражения (2.5), приводит к равенству:
. Использование для одностороннего тока выражения (2.5), приводит к равенству:
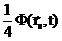 +
+ 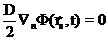 . Из которого получается искомое условие на границе среда-вакуум:
. Из которого получается искомое условие на границе среда-вакуум: 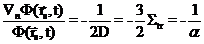 , где комплекс, стоящий в левой части уравнения часто называют логарифмической производной, а величину
, где комплекс, стоящий в левой части уравнения часто называют логарифмической производной, а величину 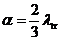 - длиной линейной экстраполяции плотности потока в вакуум. Для выяснения смысла этого названия рассмотрим одномерную плоскую геометрию - рисунок 4.
- длиной линейной экстраполяции плотности потока в вакуум. Для выяснения смысла этого названия рассмотрим одномерную плоскую геометрию - рисунок 4.

 |

 СРЕДА ВАКУУМ
СРЕДА ВАКУУМ
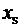
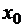 X
X
Рис.4 Иллюстрация понятия длины линейной экстраполяции потока в вакуум
Экстраполируем линейно функцию плотности потока, которая определена внутри среды, в вакуум. Необходимо подчеркнуть, что выполненная линейная экстраполяция не имеет никакого отношения к описанию нейтронного поля в вакууме, это просто удобный математический прием. Используем полученное выше условие на границе среда-вакуум (точка 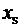 на рисунке 4) для одномерной плоской геометрии:
на рисунке 4) для одномерной плоской геометрии: 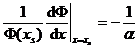 .
.
Найдем значение 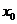 при котором функция, описывающая при
при котором функция, описывающая при 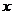
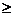
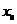 линейную экстраполяцию потока в вакуум:
линейную экстраполяцию потока в вакуум: 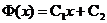 , обращается в ноль. Для этого получим систему линейных уравнений, первое из которых определяет обращение в ноль
, обращается в ноль. Для этого получим систему линейных уравнений, первое из которых определяет обращение в ноль 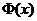 при
при 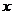 =
= 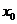 :
: 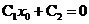 , а второе - условие на границе среда-вакуум, написанное выше:
, а второе - условие на границе среда-вакуум, написанное выше: 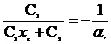 . Решив эту систему уравнений, получим:
. Решив эту систему уравнений, получим: 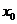 =
= 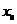 +
+ 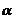 . Таким образом, длина линейной экстраполяции плотности потока в вакуум - это расстояние от границы среды и вакуума на котором плотность потока нейтронов обращается в ноль при ее линейной экстраполяции от границы среды в вакуум. А воображаемая граница, на которой функция, линейно экстраполирующая поток в вакуум, обращается в ноль называется экстраполированной границей среда-вакуум.
. Таким образом, длина линейной экстраполяции плотности потока в вакуум - это расстояние от границы среды и вакуума на котором плотность потока нейтронов обращается в ноль при ее линейной экстраполяции от границы среды в вакуум. А воображаемая граница, на которой функция, линейно экстраполирующая поток в вакуум, обращается в ноль называется экстраполированной границей среда-вакуум.
В диффузионном приближении часто ставят условие равенства плотности потока нулю на экстраполированной границе среда-вакуум: 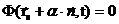 .
.
Поскольку диффузионное приближение применимо для описания нейтронного поля в средах, размер которых много больше длины свободного пробега нейтрона, то добавкой 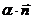 часто пренебрегают и используют условие равенства потока нулю на границе среды и вакуума. При этом, естественно, точность описания нейтронного потока около границы еще более ухудшается, но это не оказывает существенного влияния на точность описания нейтронного поля на расстояниях более 3-х длин свободного пробега нейтрона от границы.
часто пренебрегают и используют условие равенства потока нулю на границе среды и вакуума. При этом, естественно, точность описания нейтронного потока около границы еще более ухудшается, но это не оказывает существенного влияния на точность описания нейтронного поля на расстояниях более 3-х длин свободного пробега нейтрона от границы.
Используя более точные приближения, чем диффузионное, можно показать, что для обеспечения наилучшей точности описания плотности потока нейтронов внутри среды в рамках диффузионного приближения, длину линейной экстраполяции плотности потока в вакуум надо рассчитывать не как 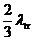 , а как
, а как 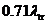 .
.
Условие локализованного источника. Рассмотрим среду, в которой в точке 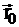 расположен точечный источник мощностью
расположен точечный источник мощностью 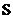 [1/c]. Перепишем уравнение (2.3) для случая стационарной задачи и данного вида источника:
[1/c]. Перепишем уравнение (2.3) для случая стационарной задачи и данного вида источника:
- 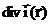 -
- 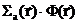 +
+ 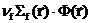 +
+ 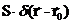 = 0,
= 0,
где 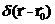 - дельта функция Дирака, которая равна единице, если
- дельта функция Дирака, которая равна единице, если 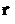 =
= 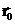 , и нулю - в противном случае. Окружим источник сферой, радиуса R с центром в точке расположения источника, проинтегрируем последнее равенство по объему получившегося шара и возьмем предел при стремлении радиуса шара к нулю:
, и нулю - в противном случае. Окружим источник сферой, радиуса R с центром в точке расположения источника, проинтегрируем последнее равенство по объему получившегося шара и возьмем предел при стремлении радиуса шара к нулю:
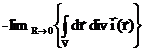
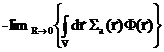 +
+ 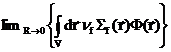 + +
+ + 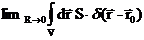 =
= 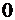
Во втором и третьем членах в левой части уравнения стоят интегралы от ограниченных функций при стремлении области интегрирования к нулю, так как объем шара бесконечно малого радиуса равен нулю. Предел от этих интегралов равен нулю. Интеграл от последнего члена в левой части равен 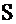 . В первом же члене перейдем от интеграла по объему шара к интегралу по его поверхности Г. В результате получим следующее условие локализованного источника:
. В первом же члене перейдем от интеграла по объему шара к интегралу по его поверхности Г. В результате получим следующее условие локализованного источника: 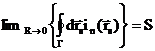 . В левой части этого равенства стоит выражение, которое равно числу нейтронов, которые пересекают в единицу времени поверхность сферы бесконечно малого радиуса, окружающей источник. Естественно, что это число нейтронов равно мощности внешнего источника.
. В левой части этого равенства стоит выражение, которое равно числу нейтронов, которые пересекают в единицу времени поверхность сферы бесконечно малого радиуса, окружающей источник. Естественно, что это число нейтронов равно мощности внешнего источника.
если в бесконечной однородной гомогенной среде действует I точечных источников нейтронов различной мощности (рисунок 6), то поток нейтронов в точке 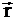 будет определяться выражением:
будет определяться выражением:
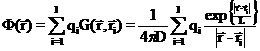

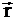
 *q1
*q1
 *q2
*q2

 *q3
*q3
.
.
.

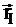 *qI
*qI
Рис.6 Расположение точечных источников в среде
Если в среде существует область 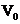 , в которой находится распределенный источник нейтронов мощностью
, в которой находится распределенный источник нейтронов мощностью 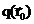 , то, согласно принципу суперпозиции источников, поток нейтронов в точке
, то, согласно принципу суперпозиции источников, поток нейтронов в точке 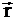 будет определяться выражением:
будет определяться выражением:
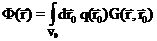 , где конкретный вид функций Грина будет определяться постановкой задачи.
, где конкретный вид функций Грина будет определяться постановкой задачи.
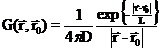 - диффузионная функция влияния (диффузионная функция Грина) точечного источника в бесконечной не размножающей гомогенной среде;
- диффузионная функция влияния (диффузионная функция Грина) точечного источника в бесконечной не размножающей гомогенной среде;
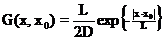 - диффузионная функция влияния (диффузионная функция Грина) плоского источника в бесконечной не размножающей гомогенной среде;
- диффузионная функция влияния (диффузионная функция Грина) плоского источника в бесконечной не размножающей гомогенной среде;
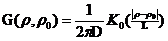 - диффузионная функция влияния (диффузионная функция Грина) нитевидного источника в бесконечной не размножающей гомогенной среде.
- диффузионная функция влияния (диффузионная функция Грина) нитевидного источника в бесконечной не размножающей гомогенной среде.
В качестве иллюстрации применения принципа суперпозиции источников, рассмотрим задачу о нахождении плотности потока нейтронов от плоского источника, используя известную функцию плотности потока от точечного источника (рисунок 7).
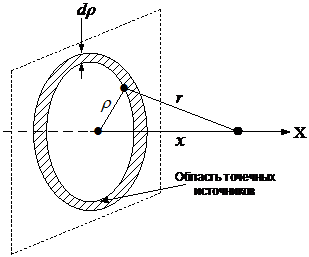
Рис.7 Схема к примеру использования принципасуперпозиции источников
Поток нейтронов в точке x от точечного источника единичной мощностью, расположенного в любой точке на окружности радиуса r, определяется выражением
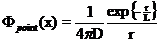 , где r - расстояние от окружности то точки х (рисунок 7).
, где r - расстояние от окружности то точки х (рисунок 7).
Представим плоский источник как совокупность точечных источников. Для этого выделим на плоскости элементарное кольцо радиуса r и толщиной dr. Это кольцо представляет собой источник нейтронов мощностью S(r)=(2prdr)q [н/с], где q[н/(см2с)] - мощность плоского источника. Поток нейтронов в точке x от элементарного кольца будет определяться выражением: 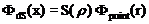 ,
,
а от всей плоскости - выражением: 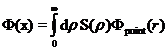 =
= 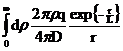 .
.
С учетом очевидной связи r2 = r2+x2, после перехода от интегрирования по переменной r к интегрированию по переменной r, это равенство принимает вид:
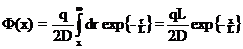 , что совпадает с полученным ранее выражением.
, что совпадает с полученным ранее выражением.
Контрольные вопросы.
1. В чем заключаются основные приближения модели диффузии моноэнергетических нейтронов?
2. Можно ли использовать уравнение диффузии моноэнергетических нейтронов для описания нейтронного поля в среде, состоящей из чистого водорода?
3. Когда можно использовать закон Фика и уравнение диффузии моноэнергетических нейтронов?
4. Сформулируйте условия выбора однозначного решения уравнения диффузии в физических задачах. Какие из этих условий являются точными, а какие приближенными?
5. Какой физический смысл имеет величина “длина диффузии”?
6. Что такое диффузионные функции влияния и где они используются?
7. Что такое альбедо и как с помощью него ставится условие на границе активная зона и отражатель?
8. Сравните альбедо плоского и сферического слоев одинаковой толщины.
9. Как изменится альбедо плоского слоя, если между отражателем и размножающей средой ввести слой вакуума?
10. Как изменится альбедо сферического слоя, если между отражателем и размножающей средой ввести слой вакуума?
11. Какой параметр определяется в экспоненциальном опыте?
12. На рисунках приведено решение уравнения диффузии моноэнергетических нейтронов в плоском слое при условии, что внешняя граница среда-вакуум считается экстраполированной. Какие из приведенных графиков соответствуют данной постановке задачи?
Дата добавления: 2018-05-02; просмотров: 2051; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
