Приложение к кинематике манипулятора
Рассмотрим задачу, подобную предыдущей и имеющей приложение в теории манипуляторов. Предположим, что и среда таких, что каждая последующая + 1-ая среда движется вместе с -ой средой и относительно -ой среды. Некоторая т.М находится в н-ой среде и движется вместе с ней и относительно ее. Нужно определить координаты, скорость и ускорение т.  в неподвижной нулевой среде, если известны положения каждой среды относительно предыдущей, координаты скорости и ускорения т.
в неподвижной нулевой среде, если известны положения каждой среды относительно предыдущей, координаты скорости и ускорения т.  в n-ой среде, скорости и ускорения каждой среды относительно предыдущей. Введем прямоугольные координаты
в n-ой среде, скорости и ускорения каждой среды относительно предыдущей. Введем прямоугольные координаты  ,
, 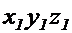 ,
,  ,…,
,…, 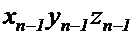 ,
, 
связав их с каждой из  сред, как показано на Фиг. 9.
сред, как показано на Фиг. 9.
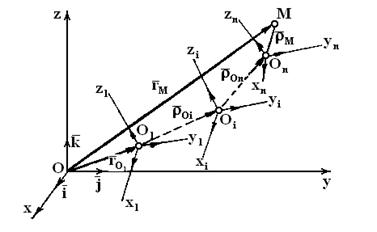
Фиг. 9.
Из построения на фиг. 9 следует:
 (1.18)
(1.18)
где
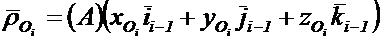 (1.19)
(1.19)
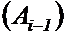 – матрица перехода от
– матрица перехода от 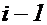 –ой системы координат к нулевой,
–ой системы координат к нулевой, 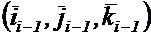 —орты
—орты 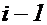 –ой координатной системы, - проекции радиус-вектора
–ой координатной системы, - проекции радиус-вектора 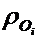 на оси
на оси 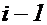 –ой координатной системы.
–ой координатной системы.
Дифференцируя выражение (1.18) с учетом (1.19) можно найти абсолютную скорость и ускорение т.  , но такой путь приведет к громоздким выражениям. Поэтому поступим так: рассмотрим движение n-ой среды относительно (n-1) –ой, отвлекаясь от всех остальных движений. Очевидно, что в этом случае имеют место установленные выше в параграфе 3 соотношения:
, но такой путь приведет к громоздким выражениям. Поэтому поступим так: рассмотрим движение n-ой среды относительно (n-1) –ой, отвлекаясь от всех остальных движений. Очевидно, что в этом случае имеют место установленные выше в параграфе 3 соотношения:
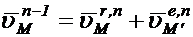 (1.20)
(1.20)
 (1.21)
(1.21)
|
|
|
Теперь рассмотрим движение n-1 –ой среды относительно n-2 –ой. Тогда определенные выражениями (1.20) и (1.21) параметры движения представят относительную скорость и ускорение т.  в n-1 –ой среде
в n-1 –ой среде
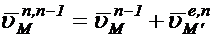 ,
, 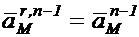 (1.22)
(1.22)
Записав выражения, аналогичные (1.20) и (1.21) для n-2 –ой среды с учетом (1.22) получим:
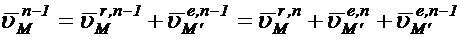 (1.23)
(1.23)
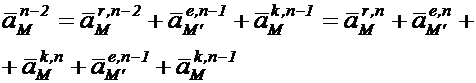 (1.24)
(1.24)
Из (1.23) и (1.24) уже ясен закон образования выражения для скорости и ускорения т.  в любой i-ой среде. Тогда для нулевой среды:
в любой i-ой среде. Тогда для нулевой среды:
 (1.25)
(1.25)
Исследование плоских механизмов 2-го класса
Для уяснения содержания кинематической теории Кориолиса и усвоения приемов ее использования разберем ряд задач из курса ТММ.
Пример 1. Начнем с простейшего случая. Тело 1 совершает сложное плоское движение, двигаясь поступательно со скоростью  и ускорением
и ускорением 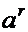 по прямолинейной направляющей (кулисе) 2, которая вращается относительно т.
по прямолинейной направляющей (кулисе) 2, которая вращается относительно т. 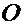 с угловой скоростью
с угловой скоростью 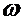 . Нужно определить скорость и ускорение т.
. Нужно определить скорость и ускорение т.  и т.
и т. 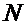 принадлежащих этому телу (Фиг.10).
принадлежащих этому телу (Фиг.10).

Фиг. 10
Выберем неподвижную систему координат 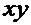 и подвижную
и подвижную 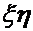 , связав ее с кулисой. Очевидно, что ускорений т.
, связав ее с кулисой. Очевидно, что ускорений т.  и т.
и т. 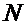 определяются выражениями (1.27) и (1.28):
определяются выражениями (1.27) и (1.28):
|
|
|
 (1.27)
(1.27)
 (1.28)
(1.28)
Правые части выражений (1.27) и (1.28) отличаются только переносными ускорениями 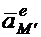 и
и 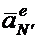 , т.к. т.
, т.к. т.  и т.
и т. 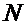 расположены в разных местах подвижной среды. Относительные ускорения и кориолисовы ускорения для т.
расположены в разных местах подвижной среды. Относительные ускорения и кориолисовы ускорения для т.  и т.
и т. 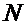 равны, т.к. в относительном движении тело движется поступательно, а угловая скорость переносного движения для обеих точек одна и та же.
равны, т.к. в относительном движении тело движется поступательно, а угловая скорость переносного движения для обеих точек одна и та же.
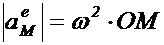 ,
,  ,
,
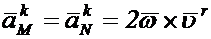 ,
,  .
.
Графические построения, соответствующие выражениям (1.27) и (1.28)
Приведены на фиг. 10.
Пример 2.Часто встречаются задачи, когда известно абсолютное ускорение, требуется определить переносное и относительное ускорения. Из выражения (1.27) получаем:
 (1.29)
(1.29)
Иногда это выражение записывают так:
 (1.30)
(1.30)
Очевидно, что в выражении (1.30) фигурируют не относительное и кориолисово ускорения, а векторы, равные им, но противоположные. Разъяснение этого обстоятельства в руководствах по ТММ часто отсутствует, что значительно затрудняет читателей. Рассмотрим механизм на Фиг. 11. Считаем, что абсолютное ускорение т. 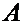 задано.
задано.
|
|
|
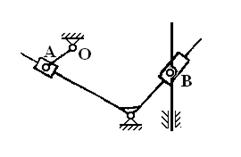
Фиг.11.
Применив два раза теорему Кориолиса, имеем:
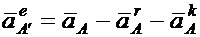
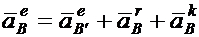
Уравнения решаются с помощью наложенных на движение звеньев связей.
Пример 3. Как показывает практика, наибольшие затруднения у учащихся возникают при кинематическом анализе рычажных механизмов с поступательными парами. Рассмотрим несколько примеров таких «трудных» механизмов.
Механизмы по схемам а, б, в и г на Фиг.12 совершенно идентичны.

Фиг.12.
Затруднения возникают в связи с тем, что учащиеся не могут найти «внутреннюю» точку диады, как это рекомендуется в некоторых пособиях по ТММ. Такой точки для поступательной пары действительно нет. Точки, принадлежащие различны элементам поступательной пары, не являются общими, т.к. движутся по-разному. Такая точка имеется лишь во вращательной паре – это ее центр. Эта задача решается только через «внешнюю» точку диады. Из выражения для ускорения точки 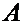 в сложном движении следует:
в сложном движении следует:

В правой части уравнения записаны известные величины, в левой части — неизвестные. Уравнение решается, т.к. нормальная составляющая переносного ускорения т.  принадлежит переносной системе, связанной со звеном 3 и совпадающей в данный момент с т.
принадлежит переносной системе, связанной со звеном 3 и совпадающей в данный момент с т. 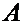 , определяется по величине
, определяется по величине  и направлению. Касательная составляющая переносного ускорения
и направлению. Касательная составляющая переносного ускорения 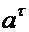 и относительное ускорение
и относительное ускорение  , известны по направлению. На Фиг.12 представлен векторный многоугольник, соответствующий записанному выше векторному уравнению. На Фиг.13 представлены частные случаи схем а и б Фиг.12. Здесь, помимо общего метода решения, можно применить еще частный метод. Рассмотрим схему а. Будем понимать под т.
, известны по направлению. На Фиг.12 представлен векторный многоугольник, соответствующий записанному выше векторному уравнению. На Фиг.13 представлены частные случаи схем а и б Фиг.12. Здесь, помимо общего метода решения, можно применить еще частный метод. Рассмотрим схему а. Будем понимать под т. 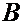 элемент кинематической пары
элемент кинематической пары 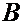 , принадлежащий звену 2. Подчеркнем, что т.
, принадлежащий звену 2. Подчеркнем, что т. 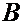 не является «внутренней» точкой диады.
не является «внутренней» точкой диады.
|
|
|

Фиг.13
Запишем выражение для ускорения т. 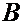 в сложном движении, происходящем за счет участия во вращении со звеном 3 и движения
в сложном движении, происходящем за счет участия во вращении со звеном 3 и движения
относительно звена 3.

Здесь 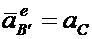 . Именно благодаря этому условию возможно частное решение.
. Именно благодаря этому условию возможно частное решение.
С другой стороны, сложное движение т. 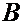 можно рассматривать происходящим за счет участия в движении звена 1 и относительно звена 1 Как будет показано в примере 5, выражение для ускорения т.
можно рассматривать происходящим за счет участия в движении звена 1 и относительно звена 1 Как будет показано в примере 5, выражение для ускорения т. 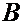 можно записать так:
можно записать так:


Записанные уравнения образую систему, решение которой представлено на Фиг.13. Путь к решению оказался более долгим, чем в общем случае,
Пример 4. Механизмы по схемам а и б Фиг.14, несмотря на внешние различия, идентичны.
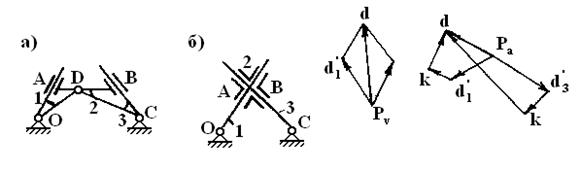
Фиг.14
Пусть нас интересует скорость и ускорение некоторой т.  . Запишем уравнения для определения скорости и ускорения т.
. Запишем уравнения для определения скорости и ускорения т.  . Запишем уравнения для определения скорости и ускорения т.
. Запишем уравнения для определения скорости и ускорения т.  в движении со звеном 1.
в движении со звеном 1.
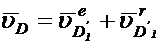
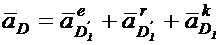
Аналогичные уравнения можно записать относительно звена 3:
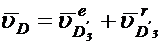
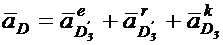
Графическое решение системы уравнений приведено на Фиг. 14. При решении уравнений использовалось очевидное свойство механизма —звенья 1 и 2 движутся с одинаковыми скоростями и ускорениями.
Благодаря этому свойству механизм применяется в качестве соединительной муфты, компенсирующей несоосность валов (муфта Ольдгейма или крестовая).
Пример 5.Специальным выбором подвижной системы координат можно упростить задачу, избавившись от кориолисова ускорения. Пусть т.
 принадлежит звену 2 кинематической цепи, представленной на Фиг.15.
принадлежит звену 2 кинематической цепи, представленной на Фиг.15.

Фиг.15.
Выберем неподвижную 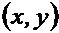 и подвижную
и подвижную 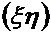 системы координат, как указано на схеме
системы координат, как указано на схеме 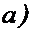 . В таком случае ускорение т.
. В таком случае ускорение т.  определяется обычным образом:
определяется обычным образом: 
Здесь 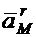 обусловлено вращением относительно осей
обусловлено вращением относительно осей 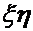 с относительной угловой скоростью
с относительной угловой скоростью 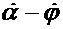 .
.
Выберем подвижные координаты по-другому: свяжем оси 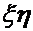 со звеном 2 (схема б). Тогда т.
со звеном 2 (схема б). Тогда т.  будет неподвижна в системе
будет неподвижна в системе 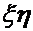 и, следовательно, кориолисово и относительное ускорения отсутствуют:
и, следовательно, кориолисово и относительное ускорения отсутствуют:
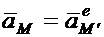
Ускорение т.  равно ускорению той т.
равно ускорению той т. 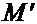 переносной системы, с которой в данный момент совпадает т.
переносной системы, с которой в данный момент совпадает т.  . Как показано в §2, переносное ускорение складывается геометрически из ускорения начала подвижных координат и ускорения, возникающего за счет вращения подвижных координат, с абсолютной угловой скоростью.
. Как показано в §2, переносное ускорение складывается геометрически из ускорения начала подвижных координат и ускорения, возникающего за счет вращения подвижных координат, с абсолютной угловой скоростью.
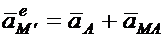
Можно выбрать подвижную систему координат еще одним специальным образом, связав ее начало с т. 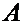 и расположив оси
и расположив оси 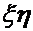 произвольным образом, но, требуя, чтобы этим осям было разрешено только поступательное движение (схема в). Таким образом, оси
произвольным образом, но, требуя, чтобы этим осям было разрешено только поступательное движение (схема в). Таким образом, оси 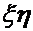 будут перемещаться по плоскости, все время оставаясь параллельными самим себе. Тогда скорость и ускорение любой точки
будут перемещаться по плоскости, все время оставаясь параллельными самим себе. Тогда скорость и ускорение любой точки 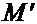 , связанной с этими осями, будет равна скорости и ускорению т.
, связанной с этими осями, будет равна скорости и ускорению т. 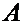 . В случае сложного движения т.
. В случае сложного движения т.  , обусловленного движением вместе с системой координат
, обусловленного движением вместе с системой координат 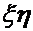 и относительно ее, кориолисово ускорение отсутствует, т.к. переносное движение поступательное. Следовательно, полное ускорение складывается из переносного ускорения т.
и относительно ее, кориолисово ускорение отсутствует, т.к. переносное движение поступательное. Следовательно, полное ускорение складывается из переносного ускорения т. 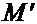 и относительного ускорения:
и относительного ускорения:

Результат совпадает с предыдущим. Это не случайно. Полученный нами результат известен под названием теоремы Ривальса: «Ускорение произвольной точки твердого тела складывается из ускорения полюса и ускорения точки в ее движении относительно полюса».
В задачах ТММ, во всех тех случаях, когда относительное движение звена осуществляется посредством вращательной кинематической пары, возможно показанное выше упрощение. Для поступательной пары такое превращение не возможно, т.к. любая точка, которую можно признать за полюс, совершает сложное движение, а, следовательно, обладает кориолисовым ускорением.
Все разнообразие четырехзвенных механизмов, представленных на Фиг.16, получено за счет различного сочетания поступательных и вращательных пар. Механизмы имеют широкое применение и носят следующие названия:
a) шарнирный четырехзвенный механизм;
б) кулисный механизм;
c) кривошипно-ползунный механизм;
д) синусный механизм;
e) механизм Ольдгейма.
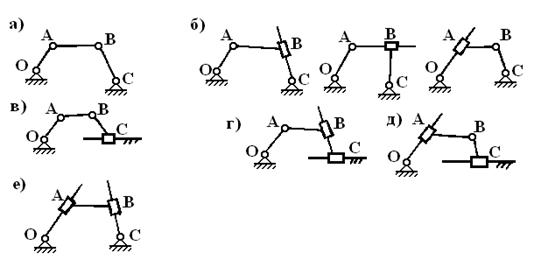
Фиг. 16
Всякий сложный механизм 2-го класса можно рассматривать как комбинацию простых четырехзвенных механизмов. Поэтому в основе кинематического анализа таких механизмов может лежать метод исследования четырехзвенного механизма.
Обобщая анализ приведённых примеров, можно придти к следующему выводу. При кинематическом анализе плоских четырехзвенных механизмов следует использовать кинематическую теорему Кориолиса. Из соответствующих уравнений для скорости и ускорения с учетом уравнений связей всегда можно найти параметры двух других движений, если задано третье движение. Так, если задано абсолютное движение, можно найти относительное и переносное, если задано относительное — то можно найти абсолютное и переносное, если задано переносное — абсолютное и относительное.
Дата добавления: 2018-05-02; просмотров: 215; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
